Гимназия №1543 из 4 в 5 класс 2023 год
Печать
youit.school ©
ЛИЦЕЙ №1543
2023 год
31.05.2023
- В записи $\star\star\star 5 : 11 = \star\star$ надо заменить звёздочки цифрами так, чтобы получилось верное равенство. Сколько решений у этой задачи?
- Андрей исписал в тетради по математике втрое меньше страниц, чем ему осталось исписать. После того, как он исписал ещё 16 страниц, количество исписанных страниц сравнялось с количеством чистых. Сколько всего страниц в тетради?
- На волшебном дереве за пять ночей выросло сто золотых монет. Сколько монет выросло в последнюю ночь, если известно, что в каждую ночь вырастало на три монеты больше, чем в предыдущую?
- Разрежьте квадрат со стороной 6 см на две равные фигуры периметра 38 см.
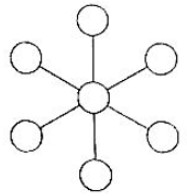
- Соня вписала в кружки числа 1, 2, 3, 4, 5, 6, 7 по одному разу так, что сумма чисел в каждой «тройке» (две крайние и центральная) одинакова. Какое число оказалось в центральном кружке? Для каждого такого числа приведите пример расстановки чисел. Объясните, почему другие числа в «серединке цветка» оказаться не могут.
- Сколько есть треугольников с вершинами в нарисованных точках?
\[
\begin{matrix}
\cdot & \cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot & \cdot
\end{matrix}
\]
- Высота комнаты 3 метра. При её ремонте выяснилось, что на каждую стену уходит краски больше, чем на пол. Может ли площадь пола этой комнаты быть больше чем 10 квадратных метров?
- Дед Мороз предложил детям угадать, сколько у него в мешке подарков.
Аня сказала: «Не больше 12».
Боря: «Не меньше 11».
Ваня: «Больше 11».
Гриша: «Меньше 10».
Сколько подарков в пакете, если правду сказал ровно один ребёнок?
- К кабинке канатной дороги, идущей в гору, подошли 8 гномов с массами 1, 1, 2, 2, 3, 3, 6, 6 в условных кг. Известно, что кабинка ходит в гору или с горы и может находиться на двух станциях. Она может возить на склонах либо одного гнома, либо двух, если их суммарная масса не превышает 7 кг. Пустая кабинка ходить не может. Как всем гномам подняться на гору?
Материалы школы Юайти
youit.school ©
Решения задач
- В записи $\star\star\star 5 : 11 = \star\star$ надо заменить звёздочки цифрами так, чтобы получилось верное равенство. Сколько решений у этой задачи?
Решение: Четырёхзначное число оканчивается на 5, делится на 11 и равно $11 \cdot \text{двузначное число}$. Единственное подходящее двузначное число — 95, так как $11 \cdot 95 = 1045$. Таким образом, запись принимает вид $1045 : 11 = 95$. Все звёздочки заменяются однозначно.
Ответ: 1 решение.
- Андрей исписал в тетради по математике втрое меньше страниц, чем ему осталось исписать. После того, как он исписал ещё 16 страниц, количество исписанных страниц сравнялось с количеством чистых. Сколько всего страниц в тетради?
Решение: Пусть изначально исписано $x$ страниц, тогда осталось $3x$. Всего страниц: $x + 3x = 4x$. После исписания 16 страниц:
$x + 16 = 3x - 16 \implies 2x = 32 \implies x = 16$.
Всего страниц: $4x = 64$.
Ответ: 64.
- На волшебном дереве за пять ночей выросло сто золотых монет. Сколько монет выросло в последнюю ночь, если известно, что в каждую ночь вырастало на три монеты больше, чем в предыдущую?
Решение: Пусть в первую ночь выросло $a_1$ монет. Это арифметическая прогрессия с разностью $d = 3$. Сумма за 5 дней:
$S_5 = \frac{2a_1 + 4 \cdot 3}{2} \cdot 5 = (a_1 + 6) \cdot 5 = 100 \implies a_1 = 14$.
Пятый член: $a_5 = a_1 + 4d = 14 + 12 = 26$.
Ответ: 26.
- Разрежьте квадрат со стороной 6 см на две равные фигуры периметра 38 см.
Решение: Периметр каждой фигуры после разреза равен 38 см. Длина разреза должна быть $L = \frac{76 - 24}{2} = 26$ см. Для этого разрез делают зигзагообразно, увеличивая длину линии разреза до 26 см. Например, многократно изгибая линию внутри квадрата.
Ответ: Разрезать квадрат зигзагом с длиной разреза 26 см.
- Соня вписала в кружки числа 1, 2, 3, 4, 5, 6, 7 по одному разу так, что сумма чисел в каждой «тройке» (две крайние и центральная) одинакова. Какое число оказалось в центральном кружке? Для каждого такого числа приведите пример расстановки. Объясните, почему другие числа в «серединке цветка» оказаться не могут.
Решение: Пусть центральное число $x$. Сумма всех троек: $6S = 6x + 2(28 - x) \implies 3S = 2x + 28$. Для целого $S$ возможны $x = 4$ ($S = 12$) и $x = 7$ ($S = 14$). Примеры:
- При $x = 4$: тройки $(1,4,7)$, $(2,4,6)$, $(3,4,5)$. - При $x = 7$: тройки $(1,7,6)$, $(2,7,5)$, $(3,7,4)$.
Другие $x$ не дают целого $S$.
Ответ: Центральное число 4 или 7.
- Сколько есть треугольников с вершинами в нарисованных точках?
\[
\begin{matrix}
\cdot & \cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot & \cdot
\end{matrix}
\]
Решение: Треугольники образуются выбором 2 точек из одного ряда и 1 из другого:
$C(5,2) \cdot C(5,1) \cdot 2 = 10 \cdot 5 \cdot 2 = 100$.
Ответ: 100.
- Высота комнаты 3 метра. При её ремонте выяснилось, что на каждую стену уходит краски больше, чем на пол. Может ли площадь пола этой комнаты быть больше чем 10 квадратных метров?
Решение: Пусть площадь пола $S = ab > 10$. Площадь каждой стены $3a > S$ и $3b > S$. Тогда $a < 3$ и $b < 3$, откуда $S = ab < 9$. Противоречие.
Ответ: Нет.
- Дед Мороз предложил детям угадать, сколько у него в мешке подарков.
Аня сказала: «Не больше 12».
Боря: «Не меньше 11».
Ваня: «Больше 11».
Гриша: «Меньше 10».
Сколько подарков в пакете, если правду сказал ровно один ребёнок?
Решение: Если правда у Ани ($N \leq 12$), то остальные лгут: $N < 11$, $N \leq 11$, $N \geq 10$. Единственное решение: $N = 10$.
Ответ: 10.
- К кабинке канатной дороги, идущей в гору, подошли 8 гномов с массами 1, 1, 2, 2, 3, 3, 6, 6 в условных кг. Известно, что кабинка ходит в гору или с горы и может находиться на двух станциях. Она может возить на склонах либо одного гнома, либо двух, если их суммарная масса не превышает 7 кг. Пустая кабинка ходить не может. Как всем гномам подняться на гору?
Решение:- 6 кг (вверх).
- 6 кг (вверх).
- 3 кг + 3 кг (вверх), вернуть 3 кг.
- 3 кг + 2 кг (вверх), вернуть 3 кг.
- 3 кг + 2 кг (вверх), вернуть 2 кг.
- 2 кг + 2 кг (вверх), вернуть 2 кг.
- 1 кг + 1 кг (вверх), вернуть 1 кг.
- 1 кг + 2 кг (вверх).
Материалы школы Юайти