8 800 707 6729
8 800 707 6729Telegram канал

Гимназия №1543 из 9 в 10 класс 2024 год

Сложность:
Дата экзамена: 06.2024
СкачатьПечать
youit.school ©

Школа № 1543 - 07.06.2024


2024


07.06.2024



  1. Упростите: \[ (a^{1.8} + 1)(a^{6/5} + a^{3/5} + 1)(a^{0.6} - 1) \]

  2. Решите систему уравнений: \[ \begin{cases} x^2 + xy + 2x + y = 7, \\ y^2 + xy + x + 2y = 11. \end{cases} \]

  3. Сумма первых семнадцати членов арифметической прогрессии равна 85, а сумма первых её двадцати одного члена равна 189.
    Сколько положительных трёхзначных чисел содержится в этой прогрессии?

  4. Какая часть площади квадрата заштрихована?


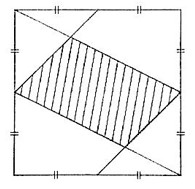
  5. В параллелограмме \(ABCD\) \(AB = 6\), \(BC = 24\), \(\angle BAD = 60^\circ\). На стороне \(BC\) параллелограмма выбрана такая точка \(M\), что \(AM = MC\). Найдите стороны треугольника \(AMD\).

  6. Каждый сотрудник фирмы выписывает две газеты, каждую газету выписывают пять человек и каждую пару газет выписывает ровно один человек. Сколько человек в фирме?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите: \[ (a^{1.8} + 1)(a^{6/5} + a^{3/5} + 1)(a^{0.6} - 1) \] Решение: Приведём степени к общему виду: \[ a^{1.8} = a^{9/5}, \quad a^{0.6} = a^{3/5} \] Обозначим \( b = a^{3/5} \). Тогда выражение преобразуется: \[ (b^3 + 1)(b^2 + b + 1)(b - 1) \] Используя формулу разности кубов: \[ (b^3 + 1)(b^2 + b + 1) = b^5 + b^4 + b^3 + b^2 + b + 1 \] Умножим на \( (b - 1) \): \[ (b^5 + b^4 + b^3 + b^2 + b + 1)(b - 1) = b^6 - 1 \] Возвращаясь к исходной переменной: \[ b^6 = (a^{3/5})^6 = a^{18/5} = a^{3.6} \] Ответ: \( a^{18/5} - 1 \).

  2. Решите систему уравнений: \[ \begin{cases} x^2 + xy + 2x + y = 7, \\ y^2 + xy + x + 2y = 11. \end{cases} \] Решение: Сложим уравнения: \[ x^2 + 2xy + y^2 + 3x + 3y = 18 \implies (x + y)^2 + 3(x + y) - 18 = 0 \] Решая квадратное уравнение относительно \( z = x + y \): \[ z^2 + 3z - 18 = 0 \implies z = 3 \text{ или } z = -6 \]
    • Случай 1: \( x + y = 3 \). Подставляем \( y = 3 - x \) в первое уравнение: \[ x^2 + x(3 - x) + 2x + (3 - x) = 7 \implies 4x = 4 \implies x = 1, \quad y = 2 \]
    • Случай 2: \( x + y = -6 \). Подставляем \( y = -6 - x \) в первое уравнение: \[ x^2 + x(-6 - x) + 2x + (-6 - x) = 7 \implies -5x = 13 \implies x = -\frac{13}{5}, \quad y = -\frac{17}{5} \]
    Ответ: \( (1; 2) \) и \( \left(-\frac{13}{5}; -\frac{17}{5}\right) \).

  3. Сумма первых семнадцати членов арифметической прогрессии равна 85, а сумма первых её двадцати одного члена равна 189. Сколько положительных трёхзначных чисел содержится в этой прогрессии?
    Решение: Используя формулы суммы арифметической прогрессии: \[ \begin{cases} \frac{17}{2}(2a_1 + 16d) = 85 \implies a_1 + 8d = 5, \\ \frac{21}{2}(2a_1 + 20d) = 189 \implies a_1 + 10d = 9. \end{cases} \] Решая систему: \[ d = 2, \quad a_1 = -11 \] Общий член прогрессии: \[ a_n = -11 + 2(n - 1) = 2n - 13 \] Условия для трёхзначных чисел: \[ 100 \leq 2n - 13 \leq 999 \implies 57 \leq n \leq 506 \] Ответ: 450 чисел.

  4. -

  5. -

  6. Каждый сотрудник фирмы выписывает две газеты, каждую газету выписывают пять человек и каждую пару газет выписывает ровно один человек. Сколько человек в фирме?
    Решение: Пусть \(k\) — количество газет. Тогда: \[ \text{Общее подписок: } 5k = 2n \implies n = \frac{5k}{2} \] Количество пар газет: \[ \binom{k}{2} = n \implies \frac{k(k - 1)}{2} = \frac{5k}{2} \implies k = 6, \quad n = 15 \] Ответ: 15 человек.
Материалы школы Юайти