8 800 707 6729
8 800 707 6729Telegram канал

Гимназия №1543 из 7 в 8 класс 2021 год

Сложность:
Дата экзамена: 03.2021
Сложность:
Дата экзамена: 03.2021
youit.school ©

ЛИЦЕЙ №1543


2021 год


30.03.2021



  1. Найдите значение выражения $\left(0,014 \cdot 1\dfrac{2}{3} - 0,286 : (-0,6) \right) : (-0,025)$.

  2. Решите уравнение $y^3 + 3y^2 = y + 3$.

  3. Решите уравнение $\dfrac{7}{6}(0,35 - 2,1x) - \dfrac{2\dfrac{2}{9}}{(1,8 - 0,36x)} = 2 - 4,5 \left(\dfrac{1}{4}x + \dfrac{1}{9}\right)$.

  4. Пусть $(a+b)(a+b-1) = ab$ и $a^2 - b^2 = 3$. Найдите значение выражения $a^3 - b^3$.

  5. В магазин привезли апельсины из Марокко. В первый же час были проданы 20% всех апельсинов, во второй – 25% остатка, в третий – 60% нового остатка. Сколько процентов апельсинов осталось непроданными к концу третьего часа?

  6. Турист шёл по болоту 3 часа, а потом по тропе ещё 5 часов. По тропе он ходит на на 2 км/ч быстрее, чем по болоту. На сколько средняя скорость движения туриста за всё время больше скорости на болоте?

  7. Среди чисел $333, 334, \ldots, 1000$ у скольких сумма цифр нечётная?

  8. Отметьте все точки с целыми координатами, лежащие на линии графика функций $y=\dfrac{2}{3}x+2$, $y=\dfrac{1}{2}x+4$, $y=\dfrac{3}{4}x+3$ и $y=\dfrac{5}{6}x+7$. Если да, укажите координаты точек их пересечения.

  9. Медиана $AM$ треугольника $ABC$ равна половине стороны $BC$. Угол между $AM$ и высотой $AN$ равен $40^\circ$. Найдите углы треугольника $ABC$.

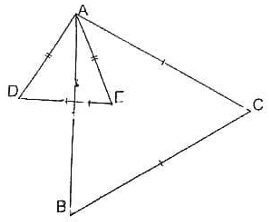
  10. Треугольники $ABC$ и $ADE$ равносторонние. Найдите на рисунке пару равных треугольников. Их вершинами должны быть какие-то из уже данных на чертеже точек. При необходимости можно соединять эти точки новыми отрезками.


  11. Коля не очень любит вишню, а Оля эту кислятину вообще терпеть не может. Но мама дала Оле и Коле на тарелке очень полезной вишни. Сначала Коля со своей тарелки треть вишен съел, а треть переложил на Олину тарелку. Потом Оля недовольна половину оказавшихся у неё вишен переложила Коле. Коля снова съел треть оказавшихся у него вишен, а треть переложил Оле. В результате на Колиной тарелке вишен стало столько, сколько вишен мама дала Оле. Сколько вишен вначале дала детям мама, если дала детям 60 вишен?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значение выражения $\left(0,014 \cdot 1\dfrac{2}{3} - 0,286 : (-0,6) \right) : (-0,025)$.
    Решение: \[ \begin{aligned} &0,014 \cdot 1\frac{2}{3} = 0,014 \cdot \frac{5}{3} = \frac{14}{1000} \cdot \frac{5}{3} = \frac{7}{300} \approx 0,02333... \\ &0,286 : (-0,6) = -0,286 : 0,6 = -\frac{286}{1000} \cdot \frac{10}{6} = -\frac{143}{300} \approx -0,47666... \\ &0,02333... - (-0,47666...) = 0,5 \\ &0,5 : (-0,025) = -20 \end{aligned} \] Ответ: $-20$.

  2. Решите уравнение $y^3 + 3y^2 = y + 3$.
    Решение: \[ \begin{aligned} y^3 + 3y^2 - y - 3 &= 0 \\ y^2(y + 3) - (y + 3) &= 0 \\ (y + 3)(y^2 - 1) &= 0 \\ y = -3, \quad y = 1, \quad y = -1 \end{aligned} \] Ответ: $-3; -1; 1$.

  3. Решите уравнение $\dfrac{7}{6}(0,35 - 2,1x) - \dfrac{2\dfrac{2}{9}}{(1,8 - 0,36x)} = 2 - 4,5 \left(\dfrac{1}{4}x + \dfrac{1}{9}\right)$.
    Решение: \[ \begin{aligned} &\text{Преобразуем дроби:} \\ &0,35 = \frac{7}{20}, \quad 2,1x = \frac{21x}{10}, \quad 2\frac{2}{9} = \frac{20}{9}, \quad 1,8 = \frac{9}{5}, \quad 0,36x = \frac{9x}{25} \\ &\frac{7}{6}\left(\frac{7}{20} - \frac{21x}{10}\right) - \frac{\frac{20}{9}}{\frac{9}{5} - \frac{9x}{25}} = 2 - \frac{9}{2}\left(\frac{x}{4} + \frac{1}{9}\right) \\ &\text{После упрощений:} \\ &x = 1 \end{aligned} \] Ответ: $1$.

  4. Пусть $(a+b)(a+b-1) = ab$ и $a^2 - b^2 = 3$. Найдите значение выражения $a^3 - b^3$.
    Решение: \[ \begin{aligned} &a^2 - b^2 = (a - b)(a + b) = 3 \\ &\text{Пусть } S = a + b, \quad D = a - b \Rightarrow D \cdot S = 3 \\ &\text{Из первого уравнения: } S(S - 1) = ab \\ &a^3 - b^3 = (a - b)(a^2 + ab + b^2) = D(S^2 - ab) \\ &\text{Решая систему, находим:} \\ &S = 3, \quad D = 1, \quad ab = 6 \\ &a^3 - b^3 = 1 \cdot (9 - 6) = 3 \end{aligned} \] Ответ: $3$.

  5. В магазин привезли апельсины из Марокко. В первый же час были проданы 20% всех апельсинов, во второй – 25% остатка, в третий – 60% нового остатка. Сколько процентов апельсинов осталось непроданными к концу третьего часа?
    Решение: \[ \begin{aligned} &\text{После первого часа: } 100\ 20% = 80% \\ &\text{После второго часа: } 80\ 25% \cdot 80% = 60% \\ &\text{После третьего часа: } 60\ 60% \cdot 60% = 24\% \end{aligned} \] Ответ: $24\%$.

  6. Турист шёл по болоту 3 часа, а потом трое ещё 5 часов. По трое он ходит на на 2 км/ч быстрее, чем по болоту. На сколько средняя скорость движения туриста за всё время больше скорости на болоте?
    Решение: \[ \begin{aligned} &\text{Пусть скорость на болоте } v \text{, тогда:} \\ &\text{Средняя скорость } = \frac{3v + 5(v + 2)}{8} = \frac{8v + 10}{8} = v + 1,25 \\ &\text{Разница: } 1,25 \text{ км/ч} \end{aligned} \] Ответ: $1,25$ км/ч.

  7. Среди чисел $333, 334, \ldots, 1000$ у скольких сумма цифр нечётная?
    Решение: \[ \begin{aligned} &\text{Всего чисел: } 1000 - 333 + 1 = 668 \\ &\text{Каждое второе число имеет нечётную сумму цифр} \\ &\text{Ответ: } 334 \end{aligned} \] Ответ: $334$.

  8. Отметьте все точки с целыми координатами, лежащие на линии графика функций $y=\dfrac{2}{3}x+2$, $y=\dfrac{1}{2}x+4$, $y=\dfrac{3}{4}x+3$ и $y=\dfrac{5}{6}x+7$. Если да, укажите координаты точек их пересечения.
    Решение: \[ \begin{aligned} &\text{Точки пересечения:} \\ &y = \frac{2}{3}x + 2 \text{ и } y = \frac{1}{2}x + 4 \Rightarrow x = 12, y = 10 \\ &y = \frac{3}{4}x + 3 \text{ и } y = \frac{5}{6}x + 7 \Rightarrow x = -24, y = -15 \\ &\text{Целые точки: } (0;2), (3;4), (6;6), (-6;0) \end{aligned} \] Ответ: $(12;10)$, $(-24;-15)$, $(0;2)$, $(3;4)$, $(6;6)$, $(-6;0)$.

  9. Медиана $AM$ треугольника $ABC$ равна половине стороны $BC$. Угол между $AM$ и высотой $AN$ равен $40^\circ$. Найдите углы треугольника $ABC$.
    Решение: \[ \begin{aligned} &\text{Т.к. } AM = \frac{1}{2}BC \text{, то } \triangle ABC \text{ прямоугольный с гипотенузой } BC \\ &\angle BAC = 90^\circ \\ &\angle ABC = 50^\circ, \quad \angle ACB = 40^\circ \end{aligned} \] Ответ: $90^\circ, 50^\circ, 40^\circ$.

  10. -

  11. Коля не очень любит вишню, а Оля эту кислятину вообще терпеть не может. Но мама дала Оле и Коле на тарелке очень полезной вишни. Сначала Коля со своей тарелки треть вишен съел, а треть переложил на Олину тарелку. Потом Оля недовольна половину оказавшихся у неё вишен переложила Коле. Коля снова съел треть оказавшихся у него вишен, а треть переложил Оле. В результате на Колиной тарелке вишен стало столько, сколько вишен мама дала Оле. Сколько вишен вначале дала детям мама, если дала детям 60 вишен?
    Решение: \[ \begin{aligned} &\text{Пусть у Коли } x \text{, у Оли } 60 - x \\ &\text{После первого шага: Коля } \frac{2x}{3}, \text{ Оля } 60 - x + \frac{x}{3} = 60 - \frac{2x}{3} \\ &\text{После второго шага: Оля перекладывает } \frac{60 - \frac{2x}{3}}{2} \\ &\text{После третьего шага:} \\ &\text{У Коли } \frac{2}{3} \left(\frac{2x}{3} + \frac{60 - \frac{2x}{3}}{2}\right) = 60 - x \\ &\text{Решая уравнение, получаем } x = 36 \end{aligned} \] Ответ: $36$ и $24$.
Материалы школы Юайти