8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 8 в 9 класс 2020 год (демовариант)

Сложность:
Дата экзамена: 2020
Сложность:
Дата экзамена: 2020
youit.school ©

ЛИЦЕЙ №1535


2020 год


Демовариант - 135 минут

Часть I.

  1. (2 балла) Вычислить $\frac{7}{15}:\left(2 \cdot 0,4-4 \cdot \frac{1}{3}\right) .$
  2. (2 балла) Решить уравнение $5 x^{2}+18 x-23=0$. В бланк ответов внести разность наибольшего и наименьшего корней данного уравнения.
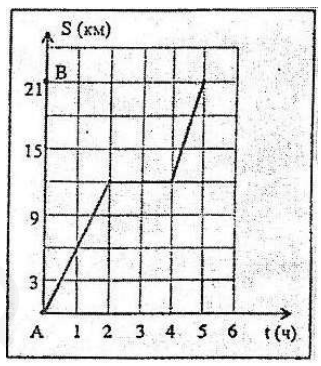
  3. (2 балла) На рисунке $(\rightarrow)$ изображён график движения туристического теплохода по озеру от города А до города В с остановкой в заповеднике. С какой скоростью (в км/ч) плыл теплоход от заповедника до города В?
  4. (3 балла) Представить выражение $\frac{8^{5} \cdot \sqrt{3^{12}}}{5 \cdot 5^{5}}$ в виде $a^{3} . \mathrm{B}$ бланк ответов внести число $\boldsymbol{a} .$
  5. (3 балла) Чему равно среднее арифметическое всех различных нулей функции $y=(17-x)\left(x^{2}+5 x\right) ?$
  6. (3 балла) Найти значение выражения $\cdot(\sqrt{6}-\sqrt{2})^{2} \cdot(8+\sqrt{48})$.
  7. (3 балла) При $\boldsymbol{x}=\mathbf{3}, \boldsymbol{y}=\mathbf{4}$ значение выражения $\frac{x y}{m x+n y}$ равно $5 .$ Найти значение этого выражения при $x=9, y=12 .$
  8. (4 балла) $\quad$ В прямоугольную трапецию вписана окружность. Точка касания окружности с боковой стороной делит эту сторону на отрезки с длинами 4 и $9 .$ Найти площадь трапеции.
  9. (4 балла) Найти значение параметра $q$, если известно, что корни $x_{1}$ и $x_{2}$ уравнения $x^{2}-4 x+q=0 \quad$ удовлетворяют условию $\quad 3 x_{1}+5 x_{2}=2 .$
  10. (4 балла) $\quad$ В растворе спирта и воды спирта в четыре раза меньше, чем воды. Когда к этому раствору добавили 20 литров воды, получили $12 \%$-ный раствор спирта. Сколько литров воды было в исходном растворе?
    Часть II.
  11. (5 баллов)
    1. Упростить выражение $\quad\left(\frac{1}{a^{2}-6 a+9}-\frac{1}{9-a^{2}}\right): \frac{1}{(3-a)^{2}}+\frac{a+9}{a+3} ;$
    2. Привести пример значения переменной $\boldsymbol{a}$, при котором данное выражение не имеет смысла.
  12. (5 баллов) Грузовик ехал по просёлочной дороге с постоянной скоростью. Из-за плохого состояния дороги ему пришлось задержаться на 6 минут. Затем грузовик увеличил скорость на 4 км/ч и ликвидировал опоздание на участке дороги протяжённостью 36 км. Найти первоначальную скорость автомобиля.
  13. (5 баллов) Дан треугольник $\mathrm{ABC}$ со сторонами $\mathrm{AB}=6 \mathrm{~cm}, \mathrm{AC}=4 \mathrm{~cm}, \mathrm{BC}=8 \mathrm{~cm} .$ Точка D лежит на стороне $A B$, а точка $E$ - на стороне $A C$, причём $A D=2 \mathrm{~cm}, A E=3 \mathrm{~cm}$. Чему равна площадь треугольника ADE?
  14. (5 баллов)
    1. Построить в одной системе координат графики функций $y=\sqrt{x} \quad$ и $\quad y=\frac{8}{x}$.
    2. С помощью построенных графиков решить уравнение $\sqrt{x}=\frac{8}{x}$;
    3. С помощью построенных графиков указать множество всех решений неравенства $\frac{8}{x}<\sqrt{x}$
    4. Найти все значения параметра $\boldsymbol{p}$, при каждом из которых прямая $y=-2 x+p \quad$ имеет с графиком функции $y=\frac{8}{x}$ ровно одну общую точку.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислить \(\frac{7}{15}:\left(2 \cdot 0,4 - 4 \cdot \frac{1}{3}\right)\).
    Решение: \(2 \cdot 0,4 = 0,8\); \(4 \cdot \frac{1}{3} = \frac{4}{3}\). \(0,8 - \frac{4}{3} = \frac{24}{30} - \frac{40}{30} = -\frac{16}{30} = -\frac{8}{15}\). \(\frac{7}{15} \div -\frac{8}{15} = -\frac{7}{8} = -0,875\). Ответ: \(-0,875\).

  2. Решить уравнение \(5x^2 + 18x - 23 = 0\).
    Решение: Дискриминант \(D = 18^2 + 4 \cdot 5 \cdot 23 = 324 + 460 = 784\). Корни: \(x = \frac{-18 \pm 28}{10}\). \(x_1 = 1\), \(x_2 = -4,6\). Разность: \(1 - (-4,6) = 5,6\). Ответ: \(5,6\).

  3. Скорость теплохода от заповедника до города В.
    Решение: Расстояние: 60 км. Время: 2 часа. Скорость: \(60 \div 2 = 30\) км/ч. Ответ: \(30\).

  4. Представить выражение \(\frac{8^5 \cdot \sqrt{3^{12}}}{5 \cdot 5^5}\) в виде \(a^3\).
    Решение: \(\frac{8^5 \cdot 3^6}{5^6} = \left(\frac{288}{25}\right)^3\). \(a = \frac{288}{25} = 11,52\). Ответ: \(11,52\).

  5. Среднее арифметическое всех различных нулей функции \(y = (17 - x)(x^2 + 5x)\).
    Решение: Нули: \(17\), \(0\), \(-5\). Среднее: \(\frac{17 + 0 - 5}{3} = 4\). Ответ: \(4\).

  6. Найти значение выражения \((\sqrt{6} - \sqrt{2})^2 \cdot (8 + \sqrt{48})\).
    Решение: \((\sqrt{6} - \sqrt{2})^2 = 8 - 4\sqrt{3}\). \((8 - 4\sqrt{3})(8 + 4\sqrt{3}) = 64 - 48 = 16\). Ответ: \(16\).

  7. Значение выражения \(\frac{xy}{mx + ny}\) при \(x = 9\), \(y = 12\).
    Решение: Из условия: \(3m + 4n = 2,4\). \(\frac{9 \cdot 12}{9m + 12n} = \frac{108}{3 \cdot 2,4} = 15\). Ответ: \(15\).

  8. Площадь прямоугольной трапеции.
    Решение: Радиус \(r = 9\). Высота \(h = 18\). Основания: \(18\) и \(13\). Площадь: \(\frac{18 + 13}{2} \cdot 18 = 279\). Ответ: \(279\).

  9. Найти параметр \(q\).
    Решение: Корни: \(x_1 = 9\), \(x_2 = -5\). \(q = 9 \cdot (-5) = -45\). Ответ: \(-45\).

  10. Количество воды в исходном растворе.
    Решение: Пусть спирта \(x\) л. Уравнение: \(\frac{x}{5x + 20} = 0,12\). \(x = 6\). Воды: \(4x = 24\) л. Ответ: \(24\).

  11. Упростить выражение и пример значения \(a\).
    Решение: \(\left(\frac{1}{(a-3)^2} + \frac{1}{(a-3)(a+3)}\right) \cdot (3 - a)^2 + \frac{a + 9}{a + 3} = 3\). Пример: \(a = 3\). Ответ: (a) \(3\); (b) \(3\).

  12. Первоначальная скорость грузовика.
    Решение: Уравнение: \(\frac{36}{v} - \frac{36}{v + 4} = 0,1\). \(v = 36\) км/ч. Ответ: \(36\).

  13. Площадь треугольника \(ADE\).
    Решение: Отношение площадей: \(\frac{1}{4}\). Площадь \(ADE = \frac{3\sqrt{15}}{4}\) см². Ответ: \(\frac{3\sqrt{15}}{4}\).

  14. Графики, уравнение, неравенство, параметр \(p\).
    Решение: (b) \(x = 4\); (c) \(x > 4\); (d) \(p = \pm 8\). Ответ: (b) \(4\); (c) \(x > 4\); (d) \(\pm 8\).
Материалы школы Юайти