8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 8 в 9 класс 2015 год

Сложность:
Дата экзамена: 2015
Печать
youit.school ©

ЛИЦЕЙ №1535


2015 год

Вариант 090114



Часть 1

  1. (2 балла). Сократите дробь и найдите ее значение при $\mathrm{x}=998 .$
    $\frac{5 x-10}{4-x^{2}}$
  2. (3 балла) Решите уравнение, в ответе запишите сумму квадратов корней.
    $\left(13-x^{2}\right) \cdot\left(5 x^{2}+3 x\right)=0$
  3. (3 балла) Вычислите:
    $-0,06 \cdot\left(-1 \frac{5}{6}\right):(2,65: 2,5-1,1)$
  4. (3 балла). Решите уравнение:
    $7 x^{2}-3 x+8=2 x^{2}-13 x+6$
    $
  5. (3 балла). Найти значение выражения:$
    $(\sqrt{7}-\sqrt{2})^{2}(9+\sqrt{56})$
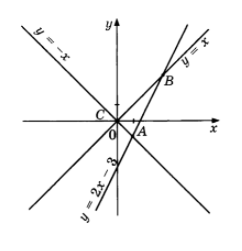
  6. (3 балла). Вычислите координаты точки А.
  7. (4 балла). При каком значении b один из корней уравнения $\mathrm{x}^{2}-7 \mathrm{x}+\mathrm{b}=0$ равен 13 ? Найдите другой корень уравнения. В ответе запишите значение выражения $3 \mathrm{x}_{1}+2 \mathrm{x}_{2}$, где $\mathrm{x}_{1}$ и $\mathrm{x}_{2}-$ корни квадратного уравнения.
  8. (5 баллов). Решите уравнение
    $\frac{x^{2}-12}{x^{2}-4}-\frac{x}{2-x}=1$
  9. (5 баллов). Имеется два сплава. Первый содержит 5% никеля, второй $40 \%$ никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий $25 \%$ никеля. На сколько килограммов масса первого сплава меньше массы второго?

    Часть 2
  10. (7 баллов).
    1. Упростить выражение
      $\left(\frac{42 a}{a^{2}-18 a+81}-\frac{5 a}{9-a}\right): \frac{5 a-3}{a^{2}-81}-\frac{9(a+9)}{a-9}$
    2. Привести пример переменной а при которой не имеет смысл выражение.
  11. (6 баллов). Из пункта А в пункт В, удаленный на расстояние 100 км, отправился междугородний автобус. Из-за ненастной погоды он ехал со скоростью на 10 км/ч меньшей, чем предполагалось по расписанию и поэтому прибыл в пункт В с опозданием на 30 минут. С какой скоростью должен был ехать автобус по расписанию?
  12. (6 баллов).
    1. Построить в одной системе координат графики функций $\mathrm{y}=\frac{6}{\mathrm{x}}$ и $\mathrm{y}=\mathrm{x}+1 .$
    2. С помощью построенных графиков решите систему уравнений
      $\left\{\begin{array}{c} y=\frac{6}{x} \\ y=x+1 \end{array}\right.$
    3. С помощью построенных графиков указать множество всех решений неравенства $\frac{6}{x}>x+1 .$


Материалы школы Юайти
youit.school ©

Решения задач



  1. Сократите дробь и найдите ее значение при $\mathrm{x}=998 .$ \[ \frac{5x - 10}{4 - x^2} \] Решение: \[ \frac{5(x - 2)}{-(x - 2)(x + 2)} = -\frac{5}{x + 2} \] При $x = 998$: \[ -\frac{5}{998 + 2} = -\frac{5}{1000} = -0,005 \] Ответ: $-0,005$.

  2. Решите уравнение, в ответе запишите сумму квадратов корней. \[ (13 - x^2)(5x^2 + 3x) = 0 \] Решение: \[ 13 - x^2 = 0 \Rightarrow x = \pm\sqrt{13} \] \[ 5x^2 + 3x = 0 \Rightarrow x(5x + 3) = 0 \Rightarrow x = 0 \text{ или } x = -\frac{3}{5} \] Сумма квадратов корней: \[ (\sqrt{13})^2 + (-\sqrt{13})^2 + 0^2 + \left(-\frac{3}{5}\right)^2 = 13 + 13 + 0 + \frac{9}{25} = 26,36 \] Ответ: $26,36$.

  3. Вычислите: \[ -0,06 \cdot \left(-1 \frac{5}{6}\right) : (2,65 : 2,5 - 1,1) \] Решение: \[ -0,06 \cdot \left(-\frac{11}{6}\right) = 0,11 \] \[ 2,65 : 2,5 = 1,06; \quad 1,06 - 1,1 = -0,04 \] \[ 0,11 : (-0,04) = -2,75 \] Ответ: $-2,75$.

  4. Решите уравнение: \[ 7x^2 - 3x + 8 = 2x^2 - 13x + 6 \] Решение: \[ 5x^2 + 10x + 2 = 0 \] \[ D = 100 - 40 = 60; \quad x = \frac{-10 \pm \sqrt{60}}{10} = \frac{-5 \pm \sqrt{15}}{5} \] Ответ: $\frac{-5 \pm \sqrt{15}}{5}$.

  5. Найти значение выражения: \[ (\sqrt{7} - \sqrt{2})^2(9 + \sqrt{56}) \] Решение: \[ (9 - 2\sqrt{14})(9 + 2\sqrt{14}) = 81 - (2\sqrt{14})^2 = 81 - 56 = 25 \] Ответ: $25$.

  6. Вычислите координаты точки А.
    Решение: Точка пересечения графиков $y = x - 2$ и $y = -2x + 1$: \[ x - 2 = -2x + 1 \Rightarrow 3x = 3 \Rightarrow x = 1; \quad y = 1 - 2 = -1 \] Ответ: $(1; -1)$.

  7. При каком значении $b$ один из корней уравнения $x^2 - 7x + b = 0$ равен 13? Найдите другой корень уравнения. В ответе запишите значение выражения $3x_1 + 2x_2$.
    Решение: \[ 13^2 - 7 \cdot 13 + b = 0 \Rightarrow 169 - 91 + b = 0 \Rightarrow b = -78 \] По теореме Виета: \[ x_1 + x_2 = 7 \Rightarrow x_2 = 7 - 13 = -6 \] \[ 3 \cdot 13 + 2 \cdot (-6) = 39 - 12 = 27 \] Ответ: $27$.

  8. Решите уравнение: \[ \frac{x^2 - 12}{x^2 - 4} - \frac{x}{2 - x} = 1 \] Решение: \[ \frac{x^2 - 12 + x(x + 2)}{x^2 - 4} = 1 \Rightarrow 2x^2 + 2x - 12 = x^2 - 4 \Rightarrow x^2 + 2x - 8 = 0 \] \[ x = \frac{-2 \pm \sqrt{36}}{2} = 2 \text{ или } -4 \] Проверка ОДЗ: $x \neq \pm 2$. Ответ: $-4$.

  9. Имеется два сплава. Первый содержит 5% никеля, второй 40% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
    Решение: \[ \begin{cases} x + y = 175 \\ 0,05x + 0,4y = 43,75 \end{cases} \] \[ 0,05x + 0,4(175 - x) = 43,75 \Rightarrow x = 75; \quad y = 100 \] Разница: $100 - 75 = 25$ кг. Ответ: $25$.

    1. Упростить выражение: \[ \left(\frac{42a}{a^2 - 18a + 81} - \frac{5a}{9 - a}\right) : \frac{5a - 3}{a^2 - 81} - \frac{9(a + 9)}{a - 9} \] Решение: \[ \frac{42a}{(a - 9)^2} + \frac{5a}{a - 9} = \frac{a(5a - 3)}{(a - 9)^2} \] \[ \frac{a(5a - 3)}{(a - 9)^2} \cdot \frac{(a - 9)(a + 9)}{5a - 3} - \frac{9(a + 9)}{a - 9} = \frac{a(a + 9)}{a - 9} - \frac{9(a + 9)}{a - 9} = a + 9 \] Ответ: $a + 9$ при $a \neq \pm9$.

    2. Пример переменной $a$: $a = 9$ или $a = -9$ (знаменатель обращается в ноль).


  11. Из пункта А в пункт В, удаленный на расстояние 100 км, отправился междугородний автобус. С какой скоростью должен был ехать автобус по расписанию?
    Решение: \[ \frac{100}{v - 10} - \frac{100}{v} = 0,5 \] \[ 100v - 100(v - 10) = 0,5v(v - 10) \Rightarrow v^2 - 10v - 2000 = 0 \] \[ v = \frac{10 + 90}{2} = 50 \text{ км/ч} \] Ответ: $50$ км/ч.

    1. Графики функций $y = \frac{6}{x}$ и $y = x + 1$ пересекаются в точках $(-3; -2)$ и $(2; 3)$.
    2. Решение системы: $(-3; -2)$ и $(2; 3)$.
    3. Решение неравенства $\frac{6}{x} > x + 1$: $x \in (-\infty; -3) \cup (0; 2)$.
Материалы школы Юайти