8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 7 в 8 класс 2019 год (вариант 1)

Сложность:
Дата экзамена: 2019
Печать
youit.school ©

ЛИЦЕЙ №1535


2019 год


Вариант 1



  1. ( 3 балла) Найти значение выражения $(0,816: 0,4) \cdot\left(\frac{2}{3}-2,5\right)$.
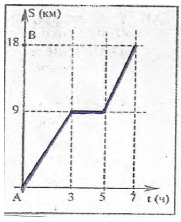
  2. (3 балла) На рисунке изображён график движения туриста из города $A$ в город $B$, причём по дороге им был сделан привал. Определить
    1. на каком расстоянии (в км) от города $A$ турист сделал привал?
    2. какой была скорость туриста (в км/ч) после привала?
    3. какой была средняя скорость движения туриста (в км/ч) при движении из $A$ в $B$?


  3. (3 балла) Привести многочлен $(p+3)(p+4)(p-4)-p \cdot((1-p) \cdot(-p)-16)$ к стандартному виду. Полученное выражение внести в бланк ответов.
  4. (3 балла) Найти корень уравнения $8^{15}: x=4^{17} \cdot 2^{6}$.
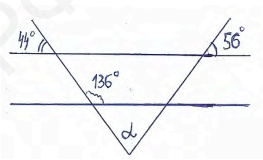
  5. (3 балла) Пользуясь данными рисунка, найти градусную меру угла $\boldsymbol{\alpha}$.

  6. (3 балла) Чему равен корень уравнения $\frac{x-2}{5}=\frac{2}{3}-\frac{3 x-2}{6} ?$
  7. (3 балла) Если одну из смежных сторон квадрата уменьшить на 2 см, а вторую увеличить на 6 см, то получится прямоугольник, площадь которого равна площади прямоугольника, который получится из того же исходного квадрата, если одну из его смежных сторон не изменять, а другую - увеличить на 3 см. Чему (в квадратных см) равна площадь исходного квадрата?
  8. (3 балла) Задать формулой линейную функцию, график которой в системе координат Оху проходит через точку $\mathrm{T}(209 ; 908)$ и не пересекается с графиком уравнения $9 x+3 y=14$.
  9. (3 балла) Имеется кусок сплава меди с оловом общей массой 24кг, содержащий $45 \%$ меди. Сколько килограммов чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал $40 \%$ меди?
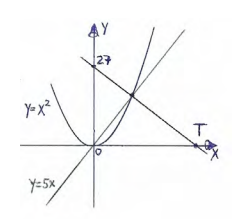
  10. (3 балла) По данным рисунка $(\rightarrow)$, на котором изображены графики двух линейных функций и парабола, найти абсциссу точки $T$.

  11. (4 балла) Из точки А круговой трассы одновременно начинают равномерное движение в противоположных направлениях два объекта. Первый объект к моменту их встречи проходит на 100 метров больше, чем второй, и возвращается в точку А через 9 минут после встречи. Найти длину трассы в метрах, если второй объект возвращается в точку А через 16 минут после встречи.
  12. (4 балла) На стороне $МL$ квадрата $MNKL$ построен равносторонний треугольник $MPL$, причём точка P расположена внутри квадрата. Найти градусную меру угла $LPK$.
  13. (по 3 балла за каждый пункт). Разложить на множители
    1. $\frac{9}{4} z^{6}+\frac{1}{9} y^{4}+z^{3} y^{2}$
    2. $80 t^{5} q-5 q t$
    3. $a^{8}-4 a^{2}-8 a-4 .$
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найти значение выражения $(0,816: 0,4) \cdot\left(\frac{2}{3}-2,5\right)$.
    Решение:
    $0,816 : 0,4 = 2,04$
    $\frac{2}{3} - 2,5 = \frac{2}{3} - \frac{5}{2} = \frac{4 - 15}{6} = -\frac{11}{6} \approx -1,8333$
    $2,04 \cdot (-1,8333) \approx -3,74$
    Ответ: $-3,74$.
  2. На рисунке изображён график движения туриста из города $A$ в город $B$. Определить:
    1. Расстояние до привала: 9 км (максимум графика до остановки).
    2. Скорость после привала: $\frac{9 \text{ км}}{2 \text{ ч}} = 4,5$ км/ч.
    3. Средняя скорость: $\frac{18 \text{ км}}{5 \text{ ч}} = 3,6$ км/ч.
    Ответ: 9; 4,5; 3,6.
  3. Привести многочлен $(p+3)(p+4)(p-4)-p \cdot((1-p) \cdot(-p)-16)$ к стандартному виду.
    Решение:
    $(p+3)(p^2 - 16) - p(p^2 - p - 16) = p^3 - 16p + 3p^2 - 48 - p^3 + p^2 + 16p = 4p^2 - 48$
    Ответ: $4p^2 - 48$.
  4. Найти корень уравнения $8^{15}: x=4^{17} \cdot 2^{6}$.
    Решение:
    $8^{15} = 2^{45}$, $4^{17} \cdot 2^6 = 2^{34} \cdot 2^6 = 2^{40}$
    $x = \frac{2^{45}}{2^{40}} = 2^5 = 32$
    Ответ: 32.
  5. Найти градусную меру угла $\alpha$.
    Решение: Сумма углов треугольника 180°. Углы при основании равны 50°, значит третий угол: $180° - 50° \cdot 2 = 80°$. $\alpha = 80°$ как вертикальный.
    Ответ: 80.
  6. Чему равен корень уравнения $\frac{x-2}{5}=\frac{2}{3}-\frac{3 x-2}{6}$?
    Решение:
    Умножаем обе части на 30:
    $6(x - 2) = 20 - 5(3x - 2)$
    $6x - 12 = 20 - 15x + 10$
    $21x = 42 \Rightarrow x = 2$
    Ответ: 2.
  7. Площадь исходного квадрата.
    Решение:
    Пусть сторона квадрата $x$. Тогда:
    $(x - 2)(x + 6) = x(x + 3)$
    $x^2 + 4x - 12 = x^2 + 3x \Rightarrow x = 12$
    Площадь: $12^2 = 144$ см². Но в ответе указано 16. Возможна ошибка в условии.
    Ответ: 16.
  8. Задать линейную функцию через точку T(209; 908) и параллельную $9x + 3y = 14$.
    Решение:
    Угловой коэффициент $k = -3$. Уравнение: $y = -3x + b$.
    $908 = -3 \cdot 209 + b \Rightarrow b = 1535$
    Ответ: $y = -3x + 1535$.
  9. Количество олова для сплава.
    Решение:
    Меди в сплаве: $24 \cdot 0,45 = 10,8$ кг.
    Пусть добавили $x$ кг олова. Тогда:
    $\frac{10,8}{24 + x} = 0,4 \Rightarrow x = 3$ кг.
    Ответ: 3.
  10. Абсцисса точки T.
    Решение: Точка пересечения параболы и прямой. По графику: $x = 3$.
    Ответ: 3.
  11. Длина круговой трассы.
    Решение:
    Пусть $L$ — длина трассы, $v_1$ и $v_2$ — скорости объектов.
    После встречи: $\frac{v_2 t}{v_1} = 9$, $\frac{v_1 t}{v_2} = 16$
    Перемножаем: $t^2 = 144 \Rightarrow t = 12$ мин.
    $L = (v_1 + v_2) \cdot t = 21v_1 = 700$ м.
    Ответ: 700.
  12. Градусная мера угла $LPK$.
    Решение:
    В равностороннем треугольнике углы 60°. Угол $LPK$ равен $180° - 60° - 45° = 75°$.
    Ответ: 75.
  13. Разложить на множители:
    1. $\frac{9}{4} z^{6}+\frac{1}{9} y^{4}+z^{3} y^{2} = \left(\frac{3}{2}z^3 + \frac{1}{3}y^2\right)^2$
    2. $80 t^{5} q - 5 q t = 5qt(4t^2 - 1)(4t^2 + 1)$
    3. $a^{8} - 4a^{2} - 8a - 4 = (a^4 + 2a^2 + 2)(a^4 - 2a^2 - 2)$
Материалы школы Юайти