Школа №1535 из 7 в 8 класс 2020 год (демоверсия)

ЛИЦЕЙ №1535

2020 год

Демовариант

1. (2 балла) Найти значение выражения $(0,816: 0,4) \cdot\left(\frac{2}{3}-2,5\right) .$
2. (2 балла) Найти корень уравнения $\frac{x-2}{5}=\frac{2}{3}-\frac{3 x-2}{6}$.
3. (2 балла) Привести многочлен $8 m-2 m \cdot(4+3 m \cdot(2-m))$ к стандартному виду и указать в бланке номер правильного ответа:
   

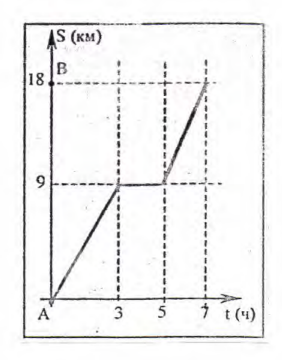
   $\mathbf{1}$	$-6 m^{3}+12 m^{2}$
   $\mathbf{2}$	$6 m^{3}-12 m^{2}$
   $\mathbf{3}$	$6 m^{2}-12 m$
   $\mathbf{4}$	$18 m^{3}-36 m^{2}+24 m$

4. (3 балла) На рисунке ( $\rightarrow$ ) изображён график движения туриста из города А в город В. Определить скорость туриста (в км/ч) после привала.
   
5. (3 балла) Упростить выражение $\left(-3 \frac{1}{3} a^{2} b\right)^{3}:\left(-1 \frac{1}{9} a^{3} b\right)^{2} .$ В бланк внести значение этого выражения при $a=7$ и $b=\frac{1}{5}$.
6. (3 балла) Упростить выражение $(7 t-3)(2 t-5)-2 \cdot(4 t-3)^{2} \quad$ и указать в бланке номер правильного ответа:
   

   $\mathbf{1}$	$-18 t^{2}+7 t-3$
   $\mathbf{2}$	$18 t^{2}-7 t+3$
   $\mathbf{3}$	$-18 t^{2}-7 t-3$
   $\mathbf{4}$	$-18 t^{2}+7 t+3$

7. (3 балла) Чему равно значение выражения $x^{4}+\frac{1}{x^{4}}$, если известно, что $x-\frac{1}{x}=3$?
8. (4 балла) Найти $\boldsymbol{a}$, при котором значение выражения $(2 a+3)(8 a-1)$ превышает соответствующее значение выражения $(5+4 a)(4 a-5)$ на $22 .$
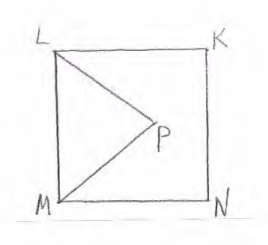
9. (4 балла) На стороне ML квадрата $MNKL$ ( $\rightarrow$ ) построен равносторонний треугольник $MPL$. Найти градусную меру угла $LPK$.
   
10. (4 балла) Имеется кусок сплава меди с оловом общей массой 24кг, содержащий $45 \%$ меди. Сколько килограммов чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал $40 \%$ меди?
    Часть II.
11. (6 баллов) Разложить на множители
    1. $2 z^{2}-36 z y+162 y^{2}$
    2. $t^{6}-16 t^{2}$
    3. $a^{4}-a^{3}-a-1 .$
12. (6 баллов) Из пункта А в пункт В, отстоящий от А на 27 км, отправился пешеход со скоростью 5 км/ч. Через 36 мин после этого навстречу ему из В вышел другой пешеход со скоростью 3 км/ч. Найти расстояние от пункта В до места их встречи.
13. (8 баллов)
    1. Построить график функции $\quad y=4 x-6$;
    2. При каком значении аргумента функция $y=4 x-6$ принимает значение, равное 2011 ?
    3. Каково взаимное расположение точки Т(-23;-99) и прямой $y=4 x-6$ : точка Т лежит на прямой, выше или ниже прямой?
    4. Найти все значения $\boldsymbol{p}$, при каждом из которых прямые $y=p^{2} \cdot x+p-8$ и $y=4 x-6$ не имеют общих точек.

Решения задач

1. Найти значение выражения $(0,816: 0,4) \cdot\left(\frac{2}{3}-2,5\right)$.
   Решение:
   $0,816 : 0,4 = 2,04$
   $\frac{2}{3} - 2,5 = \frac{2}{3} - \frac{5}{2} = \frac{4 - 15}{6} = -\frac{11}{6}$
   $2,04 \cdot \left(-\frac{11}{6}\right) = \frac{204}{100} \cdot \left(-\frac{11}{6}\right) = -\frac{2244}{600} = -3,74$
   Ответ: $-3,74$.
2. Найти корень уравнения $\frac{x-2}{5}=\frac{2}{3}-\frac{3 x-2}{6}$.
   Решение:
   Умножим обе части на 30:
   $6(x - 2) = 20 - 5(3x - 2)$
   $6x - 12 = 20 - 15x + 10$
   $6x + 15x = 30 + 12$
   $21x = 42 \quad \Rightarrow \quad x = 2$
   Ответ: 2.
3. Привести многочлен $8 m-2 m \cdot(4+3 m \cdot(2-m))$ к стандартному виду.
   Решение:
   $8m - 2m(4 + 6m - 3m^2) = 8m - 8m - 12m^2 + 6m^3 = 6m^3 - 12m^2$
   Ответ: вариант 2.
4. Определить скорость туриста после привала.
   Решение:
   После привала турист прошёл 6 км за 2 часа.
   Скорость: $\frac{6}{2} = 3$ км/ч.
   Ответ: 3.
5. Упростить выражение $\left(-3 \frac{1}{3} a^{2} b\right)^{3}:\left(-1 \frac{1}{9} a^{3} b\right)^{2}$.
   Решение:
   $\left(-\frac{10}{3}a^2b\right)^3 : \left(-\frac{10}{9}a^3b\right)^2 = -\frac{1000}{27}a^6b^3 : \frac{100}{81}a^6b^2 = -30b$
   При $a=7$, $b=\frac{1}{5}$: $-30 \cdot \frac{1}{5} = -6$
   Ответ: $-6$.
6. Упростить выражение $(7 t-3)(2 t-5)-2 \cdot(4 t-3)^{2}$.
   Решение:
   $14t^2 - 35t - 6t + 15 - 2(16t^2 - 24t + 9) = -18t^2 + 7t - 3$
   Ответ: вариант 1.
7. Найти значение выражения $x^{4}+\frac{1}{x^{4}}$, если $x-\frac{1}{x}=3$.
   Решение:
   $\left(x - \frac{1}{x}\right)^2 = 9 \quad \Rightarrow \quad x^2 + \frac{1}{x^2} = 11$
   $\left(x^2 + \frac{1}{x^2}\right)^2 = 121 \quad \Rightarrow \quad x^4 + \frac{1}{x^4} = 119$
   Ответ: 119.
8. Найти $\boldsymbol{a}$, при котором $(2 a+3)(8 a-1) - (5+4 a)(4 a-5) = 22$.
   Решение:
   $16a^2 + 22a - 3 - 16a^2 + 25 = 22$
   $22a = 0 \quad \Rightarrow \quad a = 0$
   Ответ: 0.
9. Найти градусную меру угла $LPK$.
   Решение:
   Угол $LPK$ равен $150^{\circ}$ (сумма углов квадрата и равностороннего треугольника).
   Ответ: $150^{\circ}$.
10. Найти количество олова для добавления.
    Решение:
    Меди в сплаве: $24 \cdot 0,45 = 10,8$ кг
    $10,8 = 0,4(24 + x) \quad \Rightarrow \quad x = 3$ кг
    Ответ: 3.
11. Разложить на множители:
    1. $2 z^{2}-36 z y+162 y^{2} = 2(z - 9y)^2$
    2. $t^{6}-16 t^{2} = t^2(t - 2)(t + 2)(t^2 + 4)$
    3. $a^{4}--1 =-1 =-1 = (a^2 + 1)(a^2 - a - 1)$
12. Найти расстояние от пункта В до места встречи.
    Решение:
    Первый пешеход прошёл до выхода второго: $5 \cdot 0,6 = 3$ км
    Оставшееся расстояние: $27 - 3 = 24$ км
    Время встречи: $\frac{24}{5 + 3} = 3$ часа
    Расстояние от В: $3 \cdot 3 = 9$ км
    Ответ: 9 км.
13. 1. График $y = 4x - 6$ — прямая через точки $(0; -6)$ и $(2; 2)$.
    2. $4x - 6 = 2011 \quad \Rightarrow \quad x = 504,25$
    3. При $x = -23$: $y = 4(-23) - 6 = -98$. Точка $T(-23; -99)$ ниже прямой.
    4. Прямые не пересекаются при $p^2 = 4$ и $p - 8 \neq -6 \quad \Rightarrow \quad p = -2$