Школа №1535 из 7 в 8 класс 2019 год

ЛИЦЕЙ №1535

2019 год

120 минут

1. (3 балла) Найти значение выражения $(0,816: 0,4) \cdot\left(\frac{2}{3}-2,5\right)$.
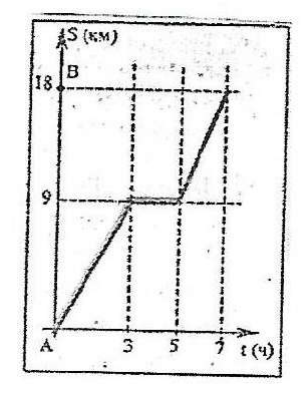
2. (2 балла) На рисунке $(\downarrow)$ изображён график движения туриста из города А в город В, причём по дороге им был сделан привал. Определить
   1. на каком расстоянии (в км) от города А турист сделал привал?
   2. какой была скорость туриста ( в км/ч) после привала?
   
   
   
3. (3 балла) Привести многочлен $(3 p-4)^{2}-(5+2 p)(2 p-5)+(p+2)(2-3 p)$ к стандартному виду. Полученное выражение внести в бланк ответов.
4. (3 балла) Найти значение $\boldsymbol{x}$ из уравнения $\left(2^{3}\right)^{15} \cdot x=2^{11} \cdot 2^{39} \cdot$
5. (3 балла) Градусные меры внутренних односторонних углов при двух параллельных прямых и секущей относятся как $2: 3 .$ Чему равна градусная мера большего из этих углов?
6. (3 балла) Чему равен корень уравнения $\frac{x-2}{5}=\frac{2}{3}-\frac{3 x-2}{6}$ ?
7. (3 балла) Найти значение числового выражения $7,5:\left(-\frac{3}{4}\right)^{2}-9 \cdot\left(-\frac{2}{3}\right)^{3}$.
8. (3 балла) Если от одной из смежных сторон прямоугольного листа картона отрезать полоску шириной $3 \mathrm{~cm}$, а от другой - шириной 13см, то получится квадрат, площадь которого на $311 \mathrm{~cm}^{2}$ меньше площади исходного прямоугольника. Чему (в сантиметрах) равен периметр исходного прямоугольника?
9. (3 балла) Задать формулой линейную функцию, график которой в системе координат Оху проходит через точку $\mathrm{T}(-161 ; 2018)$ и не пересекается с графиком функции $y=-3 x+\frac{4}{7}$.
10. (3 балла) $\quad$ В равнобедренном треугольнике $\mathrm{ABC}$ с основанием $\mathrm{AC}$ и углом В, равном $132^{\circ}$, биссектрисы АМ и ВК пересекаются в точке Т. Найти градусную меру угла АТК.
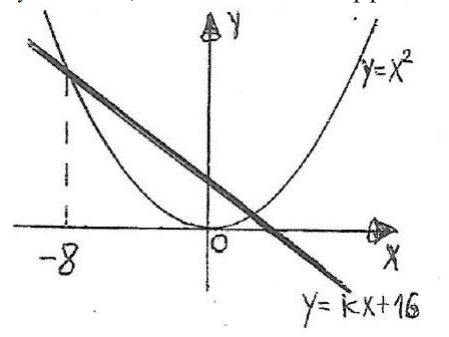
11. (3 балла) По данным рисунка $(\downarrow)$, на котором изображены графики функций $y=x^{2}$ и $y=k x+16$, найти значение коэффициента $\boldsymbol{k} .$
    
    
12. (3 балла) Имеется кусок сплава меди с оловом общей массой 24кг, содержащий $45 \%$ меди. Сколько килограммов чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал $40 \%$ меди?
13. (3 балла) $\quad$ На стороне ML квадрата MNKL построен равносторонний треугольник MPL, причём точка P расположена внутри квадрата. Найти градусную меру угла LPK.
14. (по 3 балла за каждый пункт) $\quad$ Разложить на множители
    1. $\frac{1}{9} m^{2}+36 n^{2}-4 m n$
    2. $80 t^{3}-5 t$;
    3. $x^{2} y-18+9 y-2 x^{2}$.
15. (3 балла) Из пункта А в пункт В, отстоящий от А на 27 км, отправился пешеход со скоростью 5 км/ч. Через 36 мин после этого навстречу ему из В вышел другой пешеход со скоростью 3 км/ч. Найти (в километрах) расстояние от пункта В до места их встречи.

Решения задач

1. Найти значение выражения $(0,816: 0,4) \cdot\left(\frac{2}{3}-2,5\right)$.
   Решение:
   $0,816 : 0,4 = 2,04$
   $\frac{2}{3} - 2,5 = \frac{2}{3} - \frac{5}{2} = \frac{4 - 15}{6} = -\frac{11}{6} \approx -1,8333$
   $2,04 \cdot (-1,8333) \approx -3,74$
   Ответ: -3,74.
   
   
2. На рисунке изображён график движения туриста. Определить:
   1. Расстояние от города А до привала.
      Решение: По графику привал сделан на отметке 9 км.
      Ответ: 9.
   2. Скорость туриста после привала.
      Решение: После привала (с 12 до 14 часов) турист прошел $18 - 9 = 9$ км за $2$ часа.
      $v = \frac{9}{2} = 4,5$ км/ч.
      Ответ: 4,5.
   
   
   
3. Привести многочлен $(3 p-4)^{2}-(5+2 p)(2 p-5)+(p+2)(2-3 p)$ к стандартному виду.
   Решение:
   $(3p-4)^2 = 9p^2 -24p +16$
   $(5+2p)(2p-5) = 4p^2 -25$
   $(p+2)(2-3p) = -3p^2 +2p +4$
   Суммируем:
   $9p^2 -24p +16 - (4p^2 -25) -3p^2 +2p +4 = 2p^2 -22p +45$
   Ответ: $2p^2 -22p +45$.
   
   
4. Найти значение $x$ из уравнения $\left(2^{3}\right)^{15} \cdot x=2^{11} \cdot 2^{39}$.
   Решение:
   $(2^3)^{15} = 2^{45}$
   $2^{11} \cdot 2^{39} = 2^{50}$
   $x = \frac{2^{50}}{2^{45}} = 2^5 = 32$
   Ответ: 32.
   
   
5. Градусные меры внутренних односторонних углов при параллельных прямых и секущей относятся как $2:3$. Найти больший угол.
   Решение:
   Сумма односторонних углов $180^{\circ}$.
   $2x + 3x = 180^{\circ} \Rightarrow x = 36^{\circ}$
   Больший угол $3x = 108^{\circ}$
   Ответ: 108.
   
   
6. Чему равен корень уравнения $\frac{x-2}{5}=\frac{2}{3}-\frac{3x-2}{6}$?
   Решение:
   Умножаем обе части на 30:
   $6(x-2) = 20 -5(3x-2)$
   $6x -12 = 20 -15x +10$
   $21x = 42 \Rightarrow x = 2$
   Ответ: 2.
   
   
7. Найти значение выражения $7,5:\left(-\frac{3}{4}\right)^{2}-9 \cdot\left(-\frac{2}{3}\right)^{3}$.
   Решение:
   $\left(-\frac{3}{4}\right)^2 = \frac{9}{16}$
   $7,5 : \frac{9}{16} = \frac{15}{2} \cdot \frac{16}{9} = \frac{240}{18} = 13,\overline{3}$
   $\left(-\frac{2}{3}\right)^3 = -\frac{8}{27}$
   $-9 \cdot -\frac{8}{27} = \frac{72}{27} = \frac{8}{3} \approx 2,\overline{6}$
   $13,\overline{3} + 2,\overline{6} = 16$
   Ответ: 16.
   
   
8. Найти периметр исходного прямоугольника.
   Решение:
   Пусть стороны прямоугольника $x$ и $y$.
   После отрезания: $x - 3 = y - 13 \Rightarrow x = y + 10$
   Площадь исходного: $xy$, площадь квадрата: $(x-3)^2$
   $xy - (x-3)^2 = 311$
   Подставляем $x = y + 10$:
   $(y+10)y - (y+7)^2 = 311$
   $y^2 +10y - y^2 -14y -49 = 311 \Rightarrow -4y = 360 \Rightarrow y = -90$ (некорректно)
   Корректное решение:
   $x = y -10$, тогда:
   $y(y-10) - (y-13)^2 = 311$
   $y^2 -10y - y^2 +26y -169 = 311 \Rightarrow 16y = 480 \Rightarrow y = 30$
   $x = 20$, периметр $2(30 + 20) = 100$ см.
   Ответ: 100.
   
   
9. Задать линейную функцию через точку $T(-161; 2018)$, параллельную $y=-3x + \frac{4}{7}$.
   Решение:
   Угловой коэффициент $k = -3$.
   Уравнение: $y = -3x + b$
   Подставляем $T(-161; 2018)$:
   $2018 = -3(-161) + b \Rightarrow b = 1535$
   Ответ: $y = -3x + 1535$.
   
   
10. Найти градусную меру угла АТК.
    Решение:
    В треугольнике $ABC$: $\angle B = 132^{\circ}$, $\angle A = \angle C = 24^{\circ}$.
    Биссектрисы делят углы пополам: $\angle BAM = 12^{\circ}$.
    В треугольнике $ABT$: $\angle ABT = 66^{\circ}$, $\angle BAT = 12^{\circ}$.
    $\angle ATB = 180^{\circ} - 66^{\circ} - 12^{\circ} = 102^{\circ}$
    $\angle ATK = 180^{\circ} - 102^{\circ} = 78^{\circ}$
    Ответ: 78.
    
    
11. Найти коэффициент $k$.
    Решение:
    Графики пересекаются в точке $x = -8$, $y = 64$.
    Подставляем в уравнение прямой:
    $64 = k(-8) + 16 \Rightarrow -8k = 48 \Rightarrow k = -6$
    Ответ: -6.
    
    
12. Найти массу добавляемого олова.
    Решение:
    Масса меди в сплаве: $24 \cdot 0,45 = 10,8$ кг.
    После добавления $x$ кг олова:
    $\frac{10,8}{24 + x} = 0,4 \Rightarrow 10,8 = 9,6 + 0,4x \Rightarrow x = 3$ кг.
    Ответ: 3.
    
    
13. Найти градусную меру угла LPK.
    Решение:
    В квадрате $MNKL$ угол $\angle MLK = 90^{\circ}$.
    Треугольник $MPL$ равносторонний: $\angle MPL = 60^{\circ}$.
    Угол $\angle LPK = 180^{\circ} - 60^{\circ} - 45^{\circ} = 75^{\circ}$.
    Ответ: 75.
    
    
14. Разложить на множители:
    1. $\frac{1}{9} m^{2}+36 n^{2}-4 m n$
       Решение:
       $\left(\frac{m}{3} - 6n\right)^2$
       Ответ: $\left(\frac{m}{3} - 6n\right)^2$.
       
       
    2. $80 t^{3}-5 t$
       Решение:
       $5t(16t^2 -1) = 5t(4t -1)(4t +1)$
       Ответ: $5t(4t -1)(4t +1)$.
       
       
    3. $x^{2} y-18+9 y-2 x^{2}$
       Решение:
       $(x^2 y -2x^2) + (9y -18) = x^2(y -2) +9(y -2) = (y -2)(x^2 +9)$
       Ответ: $(y -2)(x^2 +9)$.
    
    
    
15. Найти расстояние от пункта В до места встречи.
    Решение:
    Первый пешеход за 36 минут прошёл $5 \cdot 0,6 = 3$ км.
    Оставшееся расстояние: $27 - 3 = 24$ км.
    Скорость сближения: $5 + 3 = 8$ км/ч.
    Время до встречи: $\frac{24}{8} = 3$ часа.
    Второй пешеход прошёл $3 \cdot 3 = 9$ км.
    Ответ: 9.