Школа №444 из 4 в 5 класс 2023 год

444 ШКОЛА

2023 год

1. Задача 4.
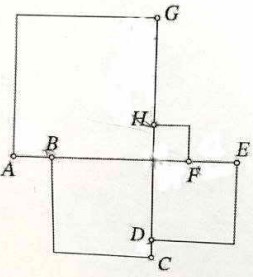
   На рисунке изображено 4 квадрата. Известно, что длина отрезка $AB = 11$, длина отрезка $FE = 13$, длина отрезка $CD = 5$. Чему равна длина отрезка $GH$?
   
   
   
   
   
   
2. Задача 5.
   Алексей, Борис, Вениамин и Григорий подозреваются в ограблении банка. Полиции удалось выяснить следующее:
   • если Григорий невиновен, то Борис виновен, а Алексей невиновен;
   • если Вениамин виновен, то Алексей и Борис невиновны;
   • если Григорий виновен, то Борис тоже виновен;
   • если Борис виновен, то кто-то из двух — Алексей и Вениамин — точно виновен.
   Отметьте тех, кто участвовал в ограблении.
   
   
3. Задача 6.
   На доске написано одно трёхзначное число и два двузначных. Сумма чисел, в записи которых есть семёрка, равна 208. А сумма чисел, в записи которых есть тройка, равна 76. Найдите сумму всех трёх чисел.

Решения задач

1. Задача 4. На рисунке изображено 4 квадрата. Известно, что длина отрезка $AB = 11$, длина отрезка $FE = 13$, длина отрезка $CD = 5$. Чему равна длина отрезка $GH$?
   Решение: Рассмотрим расположение квадратов. Каждый последующий квадрат примыкает к предыдущему таким образом, что длина стороны следующего квадрата равна сумме сторон предыдущих.
   - Сторона первого квадрата: $AB = 11$. - Сторона второго квадрата: $FE = 13$. - Сторона третьего квадрата: $CD = 5$. - Сторона четвертого квадрата $GH$ равна сумме сторон второго и третьего квадратов: $FE + CD = 13 + 5 = 18$.
   Ответ: 18.
   
   
2. Задача 5. Алексей, Борис, Вениамин и Григорий подозреваются в ограблении банка. Полиции удалось выяснить следующее:
   • если Григорий невиновен, то Борис виновен, а Алексей невиновен;
   • если Вениамин виновен, то Алексей и Борис невиновны;
   • если Григорий виновен, то Борис тоже виновен;
   • если Борис виновен, то кто-то из двух — Алексей и Вениамин — точно виновен.
   Отметьте тех, кто участвовал в ограблении.
   Решение:
   Допустим, Григорий виновен. Тогда: - По условию 3: Борис виновен. - По условию 4: Алексей или Вениамин виновен. - Если Алексей виновен, то по условию 2 Вениамин должен быть невиновен (иначе А и Б невиновны, что противоречит их виновности). - Проверка условий: - Условие 1: Григорий виновен → условие неактивно. - Условие 2: Вениамин невиновен → условие выполняется. - Условие 3: Выполняется. - Условие 4: Выполняется (Борис виновен → Алексей виновен).
   Итог: Виновны Григорий, Борис, Алексей. Вениамин невиновен.
   Ответ: Алексей, Борис, Григорий.
   
   
3. Задача 6. На доске написано одно трёхзначное число и два двузначных. Сумма чисел, в записи которых есть семёрка, равна 208. А сумма чисел, в записи которых есть тройка, равна 76. Найдите сумму всех трёх чисел.
   Решение:
   - Пусть трёхзначное число содержит цифру 7, а одно двузначное содержит 7. Тогда их сумма: $ABC + DE = 208$. - Пусть второе двузначное содержит цифру 3. Тогда сумма чисел с тройкой: $FG = 76$ (но 76 не содержит тройки → противоречие). - Альтернативно: трёхзначное число содержит 3, а одно двузначное содержит 3. Тогда сумма: $ABC + FG = 76$. - Поскольку пересечений между числами с 7 и 3 нет (иначе сумма была бы меньше), общая сумма всех трёх чисел равна $208 + 76 = 284$.
   Ответ: 284.