Школа №444 из 4 в 5 класс 2021 год

444 ШКОЛА

2021 год

21.04.2021

1. На столе в трёх банкаВх — красной, жёлтой и зелёной — стоят мёд, сахар и соль. На жёлтой написано: "Здесь не соль", на зелёной: "Соль в жёлтой банке", на красной: "Соль в зелёной банке". Оказалось, что одна надпись верная, а две — неверные. Какую банку взять, чтобы попить чаю с чем-нибудь сладким?
   
   
2. Аня, Боря, Ваня и Галя начали собирать марки. К концу четверти один из них собрал пять марок, другой — четыре, третий — три, и наконец четвёртый — только две. После того, как Боря подарил Ане на день рождения свои марки, у неё стало в два раза больше марок, чем у Гали. Сколько марок собрала Галя? Найдите все решения и объясните, почему нет других.
   
   
3. У Фёклы живут несколько кошек. Фёкла купила несколько банок с кошачьей едой. Каждая кошка съест по 5 банок, то ещё 13 банок останется. А для того, чтобы раздать кошкам по 7 банок, девяти банок не хватит. Сколько у Фёклы кошек, и сколько банок корма она купила?
   
   
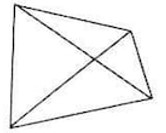
4. В четырёхугольнике диагонали делят его на 4 треугольника (см. рисунок). Известно, что сумма периметров этих треугольников равна 73 см, а периметр четырёхугольника равен 29 см. Чему равна сумма длин диагоналей?
   
   
   
5. В новогодних подарках Винни-Пуха, Пятачка и Ослика Иа было 55 пряников — у каждого не менее двух. Винни сразу же съел свои пряники. Иа-Иа своих не тронул, а Пятачок сберёг половину своих пряников и подарил их на следующий день Ослику Иа на день рождения. После этого количество пряников у Иа увеличилось в 10 раз. Сколько пряников съел Винни?
   
   
6. Семь гномов играли друг с другом в шахматы. Любые два гнома играли друг с другом не более одного раза. Известно, что Ворчун сыграл шесть партий, Тихоня — пять, Весельчак и Док — по три, Соня и Простак — по две, а Чихун — одну. С кем сыграл Весельчак?
   
   
7. Два кота — Васька и Пушок — одновременно начали есть цепочку из сосисок с разных сторон. Васька съедал в минуту на одну сосиску больше Пушка и в результате съел на 20 сосисок больше. Если бы Пушок ел с той же скоростью, а Васька ел в минуту на две сосиски больше Пушка, то Васька бы съел на 36 сосисок больше, чем Пушок. Сколько сосисок было в цепочке?

Решения задач

1. На столе в трёх банках — красной, жёлтой и зелёной — стоят мёд, сахар и соль. На жёлтой написано: "Здесь не соль", на зелёной: "Соль в жёлтой банке", на красной: "Соль в зелёной банке". Оказалось, что одна надпись верная, а две — неверные. Какую банку взять, чтобы попить чаю с чем-нибудь сладким?
   Решение: Предположим, верна надпись на жёлтой банке ("Здесь не соль"). Тогда соль не в жёлтой. Надпись на зелёной ("Соль в жёлтой") будет ложной, и на красной ("Соль в зелёной") тоже ложной. Это соответствует условию (1 верная, 2 ложные). Значит, соль в красной банке. Тогда в жёлтой и зелёной — мёд и сахар. Для сладкого подойдут жёлтая или зелёная банка. Но по условию только одна надпись верна. Если соль в красной, то зелёная банка лжёт ("Соль в жёлтой"), а красная тоже лжёт ("Соль в зелёной"). Верна только жёлтая. Значит, в жёлтой банке сахар или мёд. Гарантированно сладкое — жёлтая банка.
   Ответ: жёлтую банку.
   
   
2. Аня, Боря, Ваня и Галя начали собирать марки. К концу четверти один из них собрал пять марок, другой — четыре, третий — три, и наконец четвёртый — только две. После того, как Боря подарил Ане на день рождения свои марки, у неё стало в два раза больше марок, чем у Гали. Сколько марок собрала Галя? Найдите все решения и объясните, почему нет других.
   Решение: Пусть Галя собрала $G$ марок. После подарка у Ани стало $A + B$ марок, а у Гали осталось $G$. По условию: $A + B = 2G$. Возможные распределения марок: 5,4,3,2. Рассмотрим варианты:
   • Если $G = 4$, то $2G = 8$. Тогда $A + B = 8$. Возможные комбинации: Боря собрал 5, Аня 3. После подарка у Ани $3 + 5 = 8$, у Гали 4. Условие выполнено. Остальные: Ваня 2, Галя 4.
   • При $G = 2$: $2G = 4$. Тогда $A + B = 4$, что невозможно, так как минимальные значения Ани и Бори 2 и 3.
   • При $G = 3$: $2G = 6$. Тогда $A + B = 6$, что требует $A = 3$, $B = 3$, но марки должны быть уникальны.
   Единственное решение: Галя собрала 4 марки.
   Ответ: 4.
   
   
3. У Фёклы живут несколько кошек. Фёкла купила несколько банок с кошачьей едой. Каждая кошка съест по 5 банок, то ещё 13 банок останется. А для того, чтобы раздать кошкам по 7 банок, девяти банок не хватит. Сколько у Фёклы кошек, и сколько банок корма она купила?
   Решение: Пусть кошек $k$, банок $b$. По условию: \[ \begin{cases} 5k + 13 = b \\ 7k - 9 = b \end{cases} \] Приравниваем: $5k + 13 = 7k - 9 \Rightarrow 2k = 22 \Rightarrow k = 11$. Тогда $b = 5 \cdot 11 + 13 = 68$.
   Ответ: 11 кошек, 68 банок.
   
   
4. В четырёхугольнике диагонали делят его на 4 треугольника. Известно, что сумма периметров этих треугольников равна 73 см, а периметр четырёхугольника равен 29 см. Чему равна сумма длин диагоналей?
   Решение: Сумма периметров треугольников включает все стороны четырёхугольника и дважды диагонали. Обозначим диагонали $d_1$ и $d_2$. Тогда: \[ 29 + 2(d_1 + d_2) = 73 \Rightarrow 2(d_1 + d_2) = 44 \Rightarrow d_1 + d_2 = 22 \text{ см}. \] Ответ: 22 см.
   
   
5. В новогодних подарках Винни-Пуха, Пятачка и Ослика Иа было 55 пряников — у каждого не менее двух. Винни сразу же съел свои пряники. Иа-Иа своих не тронул, а Пятачок сберёг половину своих пряников и подарил их на следующий день Ослику Иа на день рождения. После этого количество пряников у Иа увеличилось в 10 раз. Сколько пряников съел Винни?
   Решение: Пусть у Винни $V$, Пятачка $P$, Иа $I$. Всего: $V + P + I = 55$. После подарка у Иа стало $I + \frac{P}{2} = 10I \Rightarrow \frac{P}{2} = 9I \Rightarrow P = 18I$. Поскольку $I \geq 2$, минимальное $I = 2$, тогда $P = 36$, $V = 55 - 36 - 2 = 17$. Проверка: $2 + \frac{36}{2} = 20 = 10 \cdot 2$.
   Ответ: 17 пряников.
   
   
6. Семь гномов играли друг с другом в шахматы. Любые два гнома играли друг с другом не более одного раза. Известно, что Ворчун сыграл шесть партий, Тихоня — пять, Весельчак и Док — по три, Соня и Простак — по две, а Чихун — одну. С кем сыграл Весельчак?
   Решение: Ворчун сыграл со всеми остальными (6 партий). Чихун сыграл только с Ворчуном. Тихоня не играл с Чихуном (5 партий: все, кроме Чиха). Весельчак (3 партии) мог сыграть с Ворчуном, Тихоней и Доком. Проверка: сумма партий всех гномов должна быть чётной (каждая партия учтена дважды). Сумма: 6+5+3+3+2+2+1=22 — чётно. Значит, Весельчак играл с Ворчуном, Тихоней и Доком.
   Ответ: С Ворчуном, Тихоней и Доком.
   
   
7. Два кота — Васька и Пушок — одновременно начали есть цепочку из сосисок с разных сторон. Васька съедал в минуту на одну сосиску больше Пушка и в результате съел на 20 сосисок больше. Если бы Пушок ел с той же скоростью, а Васька ел в минуту на две сосиски больше Пушка, то Васька бы съел на 36 сосисок больше, чем Пушок. Сколько сосисок было в цепочке?
   Решение: Пусть скорость Пушка $x$ сосисок/мин, тогда Васьки $x+1$. Время $t$: \[ t(x+1) - tx = t = 20 \Rightarrow t = 20 \text{ мин}. \] Общее число сосисок: $S = 20(x+1) + 20x = 40x + 20$. Во втором случае скорость Васьки $x+2$, время $t_1$: \[ t_1(x+2) - t_1x = 2t_1 = 36 \Rightarrow t_1 = 18 \text{ мин}. \] Тогда $S = 18(x+2) + 18x = 36x + 36$. Приравниваем: \[ 40x + 20 = 36x + 36 \Rightarrow 4x = 16 \Rightarrow x = 4. \] Тогда $S = 40 \cdot 4 + 20 = 180$.
   Ответ: 180 сосисок.