Гимназия №1543 из 7 в 8 класс вариант 1
Печать
youit.school ©
Разбор варианта письменной работы по математике в гимназию 1543
Задача 1. Упростите: \[ \bigl(-2\tfrac12 a^3 b\bigr)^4 \cdot 3\tfrac15 a^8 b^5. \]
Задача 2. Разложите на множители: \[ (1 - 5x)(1 + 5x) - (3x - 1)^2. \]
Задача 3. Решите уравнение: \[ \frac{1 - 2x}{3} - \frac{x + 3}{4} = \frac{2 - 4x}{5}. \]
Задача 4. Смесь спирта и воды.
В сосуде было 400 мл 80%-го раствора спирта (по объёму). Добавили 1 л чистого спирта и 1 л воды. Определите процент спирта в новом растворе.
Задача 5. Четырёхугольник $ABCD$.
Дано: $AB \parallel CD$, $AB=AD$, $BD=CD$, угол $BAD=40^\circ$. Найдите остальные углы.
Задача 6. Номер квартиры.
В доме на каждом этаже по 4 квартиры. Кв. №65 на 3-м этаже, кв. №125 — в 3-м подъезде. Где кв. №200?
Задача 1. Упростите: \[ \bigl(-2\tfrac12 a^3 b\bigr)^4 \cdot 3\tfrac15 a^8 b^5. \]
Задача 2. Разложите на множители: \[ (1 - 5x)(1 + 5x) - (3x - 1)^2. \]
Задача 3. Решите уравнение: \[ \frac{1 - 2x}{3} - \frac{x + 3}{4} = \frac{2 - 4x}{5}. \]
Задача 4. Смесь спирта и воды.
В сосуде было 400 мл 80%-го раствора спирта (по объёму). Добавили 1 л чистого спирта и 1 л воды. Определите процент спирта в новом растворе.
Задача 5. Четырёхугольник $ABCD$.
Дано: $AB \parallel CD$, $AB=AD$, $BD=CD$, угол $BAD=40^\circ$. Найдите остальные углы.
Задача 6. Номер квартиры.
В доме на каждом этаже по 4 квартиры. Кв. №65 на 3-м этаже, кв. №125 — в 3-м подъезде. Где кв. №200?
Материалы школы Юайти
youit.school ©
Разбор варианта письменной работы по математике в гимназию 1543
Задача 1. Упростите: \[ \bigl(-2\tfrac12 a^3 b\bigr)^4 \cdot 3\tfrac15 a^8 b^5. \]
Решение: \begin{align*} \bigl(-2\tfrac12 a^3 b\bigr)^4 &= \Bigl(-\frac52 a^3 b\Bigr)^4 = \frac{5^4}{2^4} a^{12}b^4 = \frac{625}{16}a^{12}b^4, \\[6pt] 3\tfrac15 a^8 b^5 &= \frac{16}{5}a^8 b^5, \\[6pt] \text{произведение}&= \frac{625}{16}a^{12}b^4 \cdot \frac{16}{5}a^8 b^5 = 625\cdot\frac{16}{16}\cdot\frac{1}{5}\,a^{20}b^9 = 125a^{20}b^9. \end{align*}
Задача 2. Разложите на множители: \[ (1 - 5x)(1 + 5x) - (3x - 1)^2. \]
Решение: \begin{align*} (1 - 5x)(1 + 5x) &= 1 - (5x)^2 = 1 - 25x^2, \\[4pt] (3x - 1)^2 &= 9x^2 - 6x + 1, \\[4pt] \text{разность}&= (1 - 25x^2) - (9x^2 - 6x + 1) = 1 - 25x^2 - 9x^2 + 6x - 1 \\[4pt] &= -34x^2 + 6x = 2x(3 - 17x). \end{align*}
Задача 3. Решите уравнение: \[ \frac{1 - 2x}{3} - \frac{x + 3}{4} = \frac{2 - 4x}{5}. \]
Решение: Умножим обе части на НОК знаменателей $60$: \[ 20(1 - 2x) - 15(x + 3) = 12(2 - 4x). \] Раскроем скобки: \[ 20 - 40x - 15x - 45 = 24 - 48x, \] Сгруппируем невязимые: \[ 20 - 45 - 40x - 15x = 24 - 48x \implies -25 - 55x = 24 - 48x \implies -55x + 48x = 24 + 25 \implies -7x = 49 \implies x = -7. \]
Задача 4. Смесь спирта и воды.
В сосуде было 400 мл 80\%-го раствора спирта (по объёму). Добавили 1 л чистого спирта и 1 л воды. Определите процент спирта в новом растворе.
Решение:
Задача 5. Четырёхугольник $ABCD$.
Дано: $AB \parallel CD$, $AB=AD$, $BD=CD$, угол $BAD=40^\circ$. Найдите остальные углы.
Решение:
Задача 6. Номер квартиры.
В доме на каждом этаже по 4 квартиры. Кв. №65 на 3-м этаже, кв. №125 — в 3-м подъезде. Где кв. №200?
Решение:
Задача 1. Упростите: \[ \bigl(-2\tfrac12 a^3 b\bigr)^4 \cdot 3\tfrac15 a^8 b^5. \]
Решение: \begin{align*} \bigl(-2\tfrac12 a^3 b\bigr)^4 &= \Bigl(-\frac52 a^3 b\Bigr)^4 = \frac{5^4}{2^4} a^{12}b^4 = \frac{625}{16}a^{12}b^4, \\[6pt] 3\tfrac15 a^8 b^5 &= \frac{16}{5}a^8 b^5, \\[6pt] \text{произведение}&= \frac{625}{16}a^{12}b^4 \cdot \frac{16}{5}a^8 b^5 = 625\cdot\frac{16}{16}\cdot\frac{1}{5}\,a^{20}b^9 = 125a^{20}b^9. \end{align*}
Задача 2. Разложите на множители: \[ (1 - 5x)(1 + 5x) - (3x - 1)^2. \]
Решение: \begin{align*} (1 - 5x)(1 + 5x) &= 1 - (5x)^2 = 1 - 25x^2, \\[4pt] (3x - 1)^2 &= 9x^2 - 6x + 1, \\[4pt] \text{разность}&= (1 - 25x^2) - (9x^2 - 6x + 1) = 1 - 25x^2 - 9x^2 + 6x - 1 \\[4pt] &= -34x^2 + 6x = 2x(3 - 17x). \end{align*}
Задача 3. Решите уравнение: \[ \frac{1 - 2x}{3} - \frac{x + 3}{4} = \frac{2 - 4x}{5}. \]
Решение: Умножим обе части на НОК знаменателей $60$: \[ 20(1 - 2x) - 15(x + 3) = 12(2 - 4x). \] Раскроем скобки: \[ 20 - 40x - 15x - 45 = 24 - 48x, \] Сгруппируем невязимые: \[ 20 - 45 - 40x - 15x = 24 - 48x \implies -25 - 55x = 24 - 48x \implies -55x + 48x = 24 + 25 \implies -7x = 49 \implies x = -7. \]
Задача 4. Смесь спирта и воды.
В сосуде было 400 мл 80\%-го раствора спирта (по объёму). Добавили 1 л чистого спирта и 1 л воды. Определите процент спирта в новом растворе.
Решение:
- исходно спирта: $400\times0.8=320$ мл, воды: $400-320=80$ мл;
- после доливки: спирта стало $320+1000=1320$ мл, воды $80+1000=1080$ мл;
- итоговый объём: $1320+1080=2400$ мл;
- процент спирта: $\frac{1320}{2400}\times100\%=55\%$.
Задача 5. Четырёхугольник $ABCD$.
Дано: $AB \parallel CD$, $AB=AD$, $BD=CD$, угол $BAD=40^\circ$. Найдите остальные углы.
Решение:
-
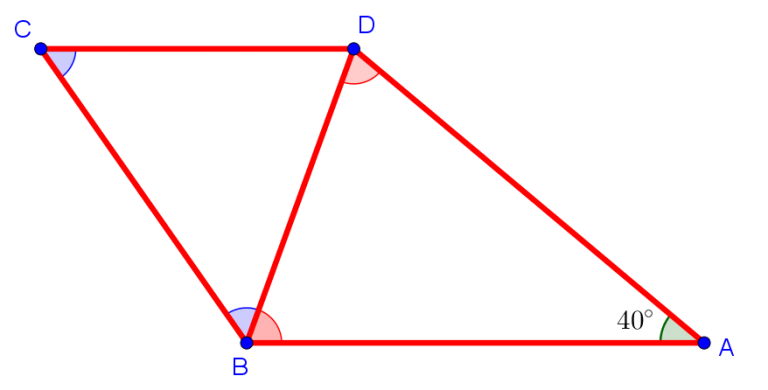
- В треугольнике $ABD$ известно $AB=AD$, значит он равнобедренный с основанием $BD$: \(\angle ABD=\angle ADB=\alpha.\) Поскольку сумма углов $\angle ABD+\angle ADB+\angle BAD=180^\circ$, то $2\alpha+40^\circ=180^\circ$, следовательно $\alpha=70^\circ$;
- Так как $AB\parallel CD$, то углы $CDA$ и $BAD$ односторонние, $\angle CDA=180^\circ-40^\circ=140^\circ$;
- В треугольнике $BCD$ известно $BD=CD$, значит он равнобедренный, и углы при основании равны: $\angle BCD=\angle CBD=\beta$. Сумма углов: $2\beta+140^\circ=180^\circ$, даёт $\beta=20^\circ$;
- Итог: $\angle A=40^\circ$, $\angle B=70^\circ$, $\angle C=20^\circ$, $\angle D=140^\circ$.
Задача 6. Номер квартиры.
В доме на каждом этаже по 4 квартиры. Кв. №65 на 3-м этаже, кв. №125 — в 3-м подъезде. Где кв. №200?
Решение:
- В подъезде не может быть меньше 44 и больше 60 кв.: 65-я в 2-м подъезде на 3-м этаже, значит в доме 14 этажей.
- В каждом подъезде по $14\times4=56$ кв. Номер 200 при делении на 56 даёт частное 3 остаток 32.
- Означает 200-я в 4-м подъезде (поскольку $3+1=4$), на 8-м этаже (так как $32/4=8$).
Материалы школы Юайти