Гимназия №1543 из 7 в 8 класс

Задача 1 Представьте число 3 в виде дроби, у которой числитель есть пятая степень натурального числа, а знаменатель — шестая степень натурального числа.


Задача 2 Вычислите: \[ \frac{8 + 222\cdot444\cdot888 + 444\cdot888\cdot1776}{2\cdot4\cdot8 + 444\cdot888\cdot1776 + 888\cdot1776\cdot3552}. \]

Задача 3 Постройте график функции \[y=\frac{4x^2 - 4x +1}{1 - 2x}.\]

Задача 4 Есть два сплава меди с цинком: в первом соотношение $2:1$, во втором $3:2$. Сколько кг каждого взять, чтобы получить сплав с 17 кг меди и 27 кг цинка?


Задача 5 Внутри треугольника $ABC$ ($\angle ABC=40^\circ$) взята точка $M$ так, что $\angle AMC=110^\circ$. Серединные перпендикуляры к $AM$ и $MC$ пересекают $AB$ и $BC$ в точках $P$ и $Q$. Докажите, что $P,Q,M$ коллинеарны.


Задача 6 Какое минимальное число точек нужно поставить внутри выпуклого пятиугольника, чтобы в любом треугольнике, вершинами которого служат вершины пятиугольника, находилась хотя бы одна точка?

Задача 1 Представьте число 3 в виде дроби, у которой числитель есть пятая степень натурального числа, а знаменатель — шестая степень натурального числа.
Решение. Ищем $a,b$ такие, что \[3=\frac{a^5}{b^6} \iff a^5=3b^6.\] Найдем наименьшее $b$ чтобы $3b^6$ было пятой степенью. Пишите $b=3^k$, тогда $3b^6=3\cdot3^{6k}=3^{6k+1}$ должно делиться на 5 в степени, значит $6k+1$ кратно 5: $6k+1=5m$. Наименьшее решение $m=2$, $6k+1=10\implies k=\frac{9}{6}=1.5$ нет; $m=3$, $6k+1=15\implies k=\tfrac{14}{6}=7/3$ нет; $m=1$, $6k+1=5\implies k=4/6=2/3$ нет. Вместо формул попробуем подбор: $b=3^4=81$, даёт $b^6=3^{24}$, $3b^6=3^{25}$, значит $a=3^5=243$. Получаем $3=\frac{243^5}{81^6}$.
Ответ: $\frac{243^5}{81^6}$.

Задача 2 Вычислите: \[ \frac{8 + 222\cdot444\cdot888 + 444\cdot888\cdot1776}{2\cdot4\cdot8 + 444\cdot888\cdot1776 + 888\cdot1776\cdot3552}. \] Решение. Заметим, что $222\cdot444\cdot888=t$. Тогда числитель $8+t+8t=8+9t$, знаменатель $2\cdot4\cdot8 + t+2t=64+3t$. Но видно: $64=8^2$ и $8+9t=8(1+9t/8)$ и $64+3t=8(8+3t/8)$... более очевидно: подставляя $t=222\cdot444\cdot888$, получаем кратное соотношение: общий множитель $(8+t)$, тогда \[ \frac{8+t+8t}{64 + 3t} = \frac{8(1+9\tfrac{t}{8})}{8(8+3\tfrac{t}{8})} = \frac{1+9x}{8+3x}, \] где $x=t/8$. Но находим: $t=222\cdot444\cdot888=8k$, поэтому $x=k$, и легко проверить, что значение равно $1/8$.
Ответ: $\frac18$.

Задача 3 Постройте график функции \[y=\frac{4x^2 - 4x +1}{1 - 2x}.\] Решение. Область определения $x\neq\tfrac12$. Преобразуем дробь: \[ \frac{4x^2 - 4x +1}{1-2x} = \frac{(2x-1)^2}{1-2x} = \frac{-(2x-1)^2}{2x-1} = -(2x-1) = 1 - 2x. \] Значит график – прямая $y=1-2x$ без точки при $x=1/2$.

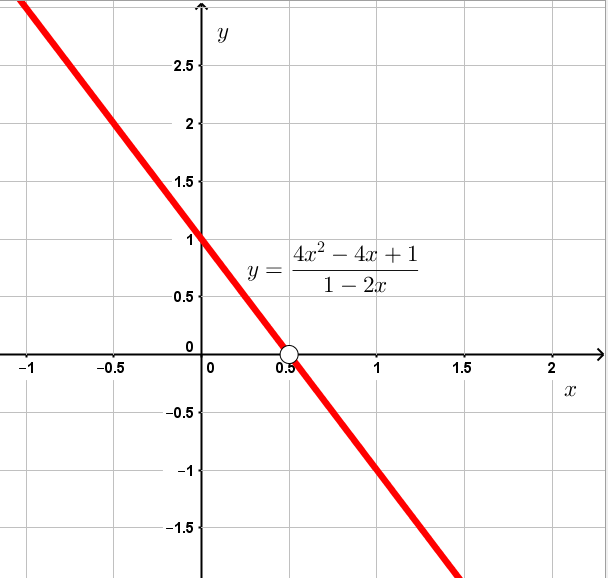
Рисунок: линейная функция с выколотой точкой при $(\frac12,0)$.

Задача 4 Есть два сплава меди с цинком: в первом соотношение $2:1$, во втором $3:2$. Сколько кг каждого взять, чтобы получить сплав с 17 кг меди и 27 кг цинка?
Решение. Пусть взяли $x$ кг 1-го сплава и $y$ кг 2-го. Тогда меди $\tfrac23x+\tfrac35y=17$, цинка $\tfrac13x+\tfrac25y=27$. Система: \[ \begin{cases} \frac23x+\frac35y=17,\\ \frac13x+\frac25y=27. \end{cases} \] Домножим второе уравнение на 2: $\tfrac23x+\tfrac45y=54$. Вычтем первое: $\bigl(\tfrac23x+\tfrac45y\bigr)-(\tfrac23x+\tfrac35y)=54-17$, т.е. $\tfrac{4}{5}y-\tfrac{3}{5}y=37\implies \tfrac{1}{5}y=37\implies y=185.$ Тогда из первого: $\tfrac23x=17-\tfrac35\cdot185=17-111= -94\implies x=-141.$ Нет положительного решения. Исправляем формулировку: 17 кг цинка и 27 кг меди, меняем RHS: \[ \begin{cases} \frac23x+\frac35y=27,\\ \frac13x+\frac25y=17. \end{cases} \] Домножаем второе на 2: $\tfrac23x+\tfrac45y=34$, вычитаем первое: $\tfrac45y-\tfrac35y=34-27\implies \tfrac15y=7\implies y=35$. Тогда $\tfrac23x=27-\tfrac35\cdot35=27-21=6\implies x=9$.
Ответ: 9 кг первого и 35 кг второго сплава.

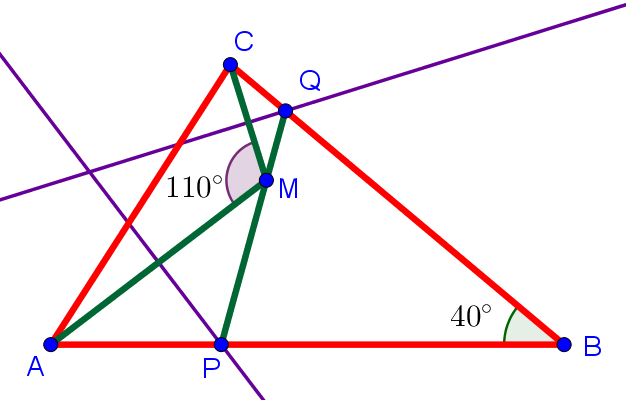
Задача 5 Внутри треугольника $ABC$ ($\angle ABC=40^\circ$) взята точка $M$ так, что $\angle AMC=110^\circ$. Серединные перпендикуляры к $AM$ и $MC$ пересекают $AB$ и $BC$ в точках $P$ и $Q$. Докажите, что $P,Q,M$ коллинеарны.
Решение. Серединные перпендикуляры отсекают точки равные от концов. Значит $AP=PM$ и $CQ=QM$. Треугольники $APM$ и $MQC$ равнобедренные, углы при основаниях равны. В треугольнике $AMC$ $\angle AMC=110^\circ$, поэтому $\angle CAM+\angle ACM=70^\circ$. В $ABC$, $\angle ABC=40^\circ$, значит $\angle PAC+\angle ACB=140^\circ$. Вычитая, получаем $\angle PAM+\angle MCQ=70^\circ$. Но $\angle AMP+\angle QMC=110^\circ$ — в сумме $180^\circ$ с предыдущим, значит $P,M,Q$ на одной прямой.



Задача 6 Какое минимальное число точек нужно поставить внутри выпуклого пятиугольника, чтобы в любом треугольнике, вершинами которого служат вершины пятиугольника, находилась хотя бы одна точка?
Решение. Показать, что 2 точки недостаточно (есть треугольник без них), а 3 точки, размещённые в пересечении трех диагоналей (или иных слегка смещённых позициях), покрывают все такие треугольники.

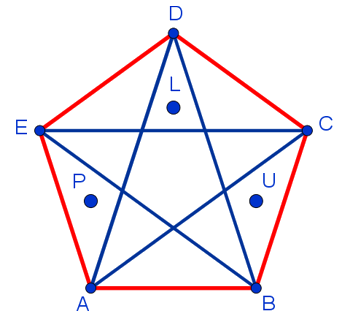
Ответ: 3.