Школа №1535 из 9 в 10 класс 2021 год вариант 1-2

ЛИЦЕЙ №1535

2021 год

1. (2 балла) Записать сумму \( 3 \cdot 10^2 + 5 \cdot 10^0 + 7 \cdot 10^{-1} + 1 \cdot 10^{-3} \) в виде десятичной дроби.
   
   
2. (а). (1 балл) Для двух бассейнов A и B график зависимости наполнения их водой изображён на рисунке (1). Через сколько минут после начала работы насосов бассейн A был заполнен на 25 тыс литров?
   
   
   
   
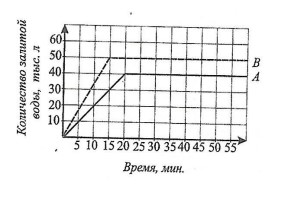
3. (б). (1 балл) Для двух бассейнов A и B график зависимости наполнения их водой изображён на рисунке (1). На сколько тысяч литров объём воды в бассейне A через 15 минут после одновременного начала наполнения бассейнов будет меньше, чем объём воды в бассейне B?
   
   
4. (2 балла) Найти значение выражения \[ \frac{(-7m^2)^3 \cdot (2n)^2}{(-14m^2n)^2}. \]
   
   
5. (3 балла) В параллелограмме меньшая сторона равна 8 см. Биссектриса острого угла параллелограмма делит большую сторону в отношении 2:1, считая от вершины тупого угла. Чему (в см) равен периметр данного параллелограмма?
   
   
6. (3 балла) Найти ординату той из общих точек графиков уравнений \( x^2 + y^2 = 5 \) и \( y = 3x + 5 \), которая имеет большую абсциссу.
   
   
7. (4 балла) Четырёхугольник \(ABCD\) вписан в окружность. Дуга \(AD\), не содержащая точек \(B\) и \(C\), составляет \(125^\circ\). Дуга \(CD\), не содержащая точек \(A\) и \(B\), составляет \(79^\circ\). Чему равна градусная мера угла \(ADC\)?
   
   
8. (4 балла) Решите уравнение \[ \frac{4}{x - 2} - \frac{4}{x + 2} = \frac{1}{2}. \] Если уравнение имеет более одного корня, то в бланк ответов внесите меньший из них.
   
   
9. (3 балла) Вычислить \[ \left( \frac{2}{7} \cdot \sqrt{ \frac{7}{1} } - \sqrt{ \frac{1}{7} } \right) \cdot \sqrt{ \frac{2}{63} }. \]
   
   
10. (3 балла) Чему равно наименьшее значение выражения \( 2x^2 + 8x + 3 \) ?
    
    
11. (4 балла) Упростить выражение \[ \left( a^3 + 2ab^2 + \frac{b^4}{a} \right) : \left( a + \frac{b^2}{a} \right) \] и найти его значение при \( a = 7 + \sqrt{5} \) и \( b = 7 - \sqrt{5} \).
    
    
12. (4 балла) В прямоугольную трапецию вписана окружность. Точка касания окружности с боковой стороной делит эту сторону на отрезки с длинами 4 и 9. Найти площадь трапеции.
    
    
13. (4 балла) Сколько килограммов спирта было выпарено из $70\%$-го раствора этого спирта с водой, если получилось 84 кг $60\%$-го раствора?
    
    
14. (4 балла) Решить систему неравенств: \[ \begin{cases} \frac{y - 1}{2} - \frac{2y + 3}{8} > y, \\ (4 + y)(y - 4) \leq 6y. \end{cases} \] Найти сумму всех различных целочисленных решений данной системы.
    
    
15. (4 балла) На изготовление 48 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 96 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час изготавливает второй рабочий?
    
    
16. (3 балла) Построить график функции \[ y = \frac{4 \cdot (x - 4) \cdot (x + 4)}{x^2 - p}. \] Пусть \( k \) — количество значений параметра \( p \), при каждом из которых уравнение \[ \frac{4 \cdot (x - 4) \cdot (x + 4)}{x^2 - p} = \frac{16 - x^2}{x} \] не имеет решений, и уравнение \[ \frac{4 \cdot (x - 4) \cdot (x + 4)}{x^2 - p} = x \] имеет единственное решение. Чему равно произведение \( k \cdot p_0 \), где \( p_0 \) — наибольшее из таких значений?
    
    
17. (4 балла) Построить график функции \[ y = \frac{4 \cdot (x - 4) \cdot (x + 4)}{x^2 - p}. \] Используя график, найдите количество различных положительных значений параметра \( p \), при которых система \[ \begin{cases} \frac{4 \cdot (x - 4) \cdot (x + 4)}{x^2 - p} > x + m \\ y = x + m \end{cases} \] имеет единственное решение.

Уточнение к №10: после упрощения выражение принимает вид $a^2 + b^2$

Уточнение к №13: \[ y \in \left(-\infty; -\frac{35}{6} \right) \iff y \in \left[ -8; -\frac{35}{6} \right) \] \[ y \in [-8; 2] \]

Уточнение к №15 (а): $p \in \{-1; 0; 1\}$

Уточнение к №15 (б): $m^* \in \{4; 5\}$

Решения задач

1. Записать сумму \(3 \cdot 10^2 + 5 \cdot 10^0 + 7 \cdot 10^{-1} + 1 \cdot 10^{-3}\) в виде десятичной дроби.
   Решение: \[ 3 \cdot 100 + 5 \cdot 1 + 7 \cdot 0,1 + 1 \cdot 0,001 = 300 + 5 + 0,7 + 0,001 = 305,701 \]
   Ответ: 305,701.
   
   
2. (а). Для двух бассейнов A и B график зависимости наполнения изображён на рисунке. Через сколько минут после начала работы насосов бассейн A был заполнен на 25 тыс литров?
   Решение: Из графика видно, что для достижения 25 тыс литров в бассейне A требуется 12,5 минут.
   Ответ: 12,5.
   
   
3. (б). Для двух бассейнов A и B найти разницу объёмов через 15 минут.
   Решение: По графику через 15 минут бассейн B содержит 60 тыс литров, а бассейн A — 40 тыс литров. Разница: \[ 60 - 40 = 20 \text{ тыс литров} \]
   Ответ: 20.
   
   
4. Найти значение выражения \(\frac{(-7m^2)^3 \cdot (2n)^2}{(-14m^2n)^2}\).
   Решение: \[ \frac{(-343m^6)(4n^2)}{196m^4n^2} = \frac{-1372m^6n^2}{196m^4n^2} = -7m^2 \]
   На значение выражения \(m^2\) не влияет, упрощаем числовые коэффициенты: \[ \frac{-1372}{196} = -7 \]
   Ответ: \(-7\).
   
   
5. Найти периметр параллелограмма, где биссектриса делит большую сторону в отношении 2:1.
   Решение: Пусть стороны \(AB = 8\) см (меньшая), \(AD\) — большая. Биссектриса делит \(AD\) на отрезки \(AK:KD = 2:1\). По свойству биссектрисы: \[ \frac{AB}{AD} = \frac{AK}{KD} = \frac{2}{1} \implies AD = 12 \text{ см} \]
   Периметр: \[ P = 2(AB + AD) = 2(8 + 12) = 40 \text{ см} \]
   Ответ: 40 см.
   
   
6. Найти ординату общей точки \(x^2 + y^2 = 5\) и \(y = 3x + 5\) с большей абсциссой.
   Решение: Подставим \(y = 3x + 5\) в окружность: \[ x^2 + (3x + 5)^2 = 5 \implies 10x^2 + 30x + 20 = 0 \] \[ x^2 + 3x + 2 = 0 \implies x = -1 \text{ или } x = -2 \]
   Большая абсцисса: \(x = -1\), тогда \(y = 3 \cdot (-1) + 5 = 2\).
   Ответ: 2.
   
   
7. Найти угол \(ADC\) вписанного четырёхугольника.
   Решение: Угол \(ADC\) вписанный и опирается на дугу \(ABC\). Мера дуги \(ABC = 360^\circ - 125^\circ - 79^\circ = 156^\circ\). Вписанный угол: \[ \angle ADC = \frac{156^\circ}{2} = 78^\circ \]
   Ответ: 78°.
   
   
8. Решить уравнение \(\frac{4}{x - 2} - \frac{4}{x + 2} = \frac{1}{2}\).
   Решение: Приведём к общему знаменателю: \[ \frac{4(x+2) - 4(x-2)}{(x-2)(x+2)} = \frac{1}{2} \implies \frac{16}{x^2 - 4} = \frac{1}{2} \] \[ x^2 - 4 = 32 \implies x^2 = 36 \implies x = \pm6 \]
   Наименьший корень: \(-6\).
   Ответ: \(-6\).
   
   
9. Вычислить выражение \(\left( \frac{2}{7} \cdot \sqrt{7} - \sqrt{\frac{1}{7}} \right) \cdot \sqrt{\frac{2}{63}}\).
   Решение: Упростим: \[ \left( \frac{2\sqrt{7}}{7} - \frac{1}{\sqrt{7}} \right) \cdot \frac{\sqrt{2}}{3\sqrt{7}} = \left( \frac{\sqrt{7}}{7} \right) \cdot \frac{\sqrt{14}}{21} = \frac{\sqrt{2}}{21} \]
   Ответ: \(\frac{\sqrt{2}}{21}\).
   
   
10. Найти наименьшее значение выражения \(2x^2 + 8x + 3\).
    Решение: Выделим полный квадрат: \[ 2(x^2 + 4x) + 3 = 2(x + 2)^2 - 5 \]
    Минимум достигается при \(x = -2\) и равен \(-5\).
    Ответ: \(-5\).
    
    
11. Упростить выражение \(\left( a^3 + 2ab^2 + \frac{b^4}{a} \right) : \left( a + \frac{b^2}{a} \right)\).
    Решение: Упростим числитель и знаменатель: \[ \frac{a^4 + 2a^2b^2 + b^4}{a} : \frac{a^2 + b^2}{a} = \frac{(a^2 + b^2)^2}{a} \cdot \frac{a}{a^2 + b^2} = a^2 + b^2 \]
    При \(a = 7 + \sqrt{5}\), \(b = 7 - \sqrt{5}\): \[ a^2 + b^2 = (7 + \sqrt{5})^2 + (7 - \sqrt{5})^2 = 2(49 + 5) = 108 \]
    Ответ: 108.
    
    
12. Найти площадь трапеции с вписанной окружностью.
    Решение: Высота \(h = 4 + 9 = 13\) см. Основания \(a\) и \(b\) связаны условием \(a + b = h +\) боковая сторона. Для прямоугольной трапеции с вписанной окружностью: \(a + b = 13 + 13 = 26\). Площадь: \[ S = \frac{a + b}{2} \cdot h = \frac{26}{2} \cdot 13 = 169 \text{ кв.см} \]
    Ответ: 169 кв.см.
    
    
13. Найти массу выпаренного спирта.
    Решение: Пусть выпарили \(m\) кг спирта. Тогда исходная масса раствора: \[ 84 + m \text{ кг}, \text{ где спирта } 0,7(84 + m) = 0,6 \cdot 84 + m \] \[ 58,8 + 0,7m = 50,4 + m \implies m = 28 \text{ кг} \]
    Ответ: 28 кг.
    
    
14. Решить систему неравенств: \[ \begin{cases} \frac{y - 1}{2} - \frac{2y + 3}{8} > y \\ (4 + y)(y - 4) \leq 6y \end{cases} \]
    Решение: \begin{align} 1)\quad 4(y-1) - (2y + 3) &> 8y \implies -6y > 7 \implies y < -\frac{7}{6} \\ 2)\quad y^2 - 6y - 16 &\leq 0 \implies y \in [-2; 8] \end{align}
    Пересечение: \( y \in [-2; -\frac{7}{6}) \). Целочисленные решения: \( y = -2 \). Сумма: \(-2\).
    Ответ: \(-2\).
    
    
15. Найти производительность второго рабочего.
    Решение: Пусть второй рабочий делает \(x\) дет./час, тогда первый — \(x + 4\). Время: \[ \frac{48}{x + 4} + 8 = \frac{96}{x} \] \[ 48x + 8x(x + 4) = 96(x + 4) \implies x = 12 \]
    Ответ: 12 дет./час.
    
    
16. Итоговые значения параметров для заданных уравнений.
    Решение (кратко): Для уникальности решений и отсутствия корней подходят \(p \in \{-1, 0, 1\}\) (количество \(k=3\)), наибольшее \(p_0=1\).
    Ответ: \(k \cdot p_0 = 3 \cdot 1 = 3\).