Школа №1535 из 9 в 10 класс 2021 год вариант 1-1
Печать
youit.school ©
ЛИЦЕЙ №1535
2021 год
- (2 балла) Найдите $65\%$ от 125.
- (2 балла) $45\%$ от числа равны 99. Найдите это число.
- (2 балла) Вычислить \[ \frac{7}{15} : \left(2 \cdot 0{,}4 - 4 \cdot \frac{1}{3} \right) \]
- (2 балла) Решить уравнение \[ \frac{x^2}{x^2 - 2x + 1} - \frac{2x}{x - 1} = 3. \] Если корней несколько, то в ответ запишите их сумму.
- (4 балла) При каких $m$ уравнение \[ m = -2 - \frac{x + 4}{x^2 + 4x} \] не имеет решения. В ответ записать сумму значений параметра $m$.
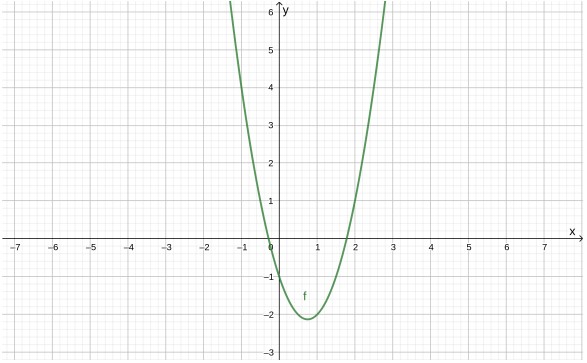
- (4 балла) Задан график квадратичной функции $y = ax^2 + bx + c$. Найдите коэффициенты $a$, $b$, $c$.
- (3 балла) Решите неравенство $(x - 4)^2(1 - x)(x + 2) \geq 0$. В ответ запишите сумму всех его целых решений.
- (3 балла) Постройте график неравенства $2|x| + 3|y| \leq 6$ и найдите площадь получившейся фигуры.
- (3 балла) Решите систему уравнений: \[ \begin{cases} x + y - 4z = 1 \\ x + 2y - 3z = 5 \\ 3x - 2y + 4z = 4 \end{cases} \]
- (3 балла) Вычислите: \[ \left( \frac{\sqrt{a + 1}}{\sqrt{a - 1}} - \frac{4 \sqrt{a}}{a - 1} \right) : \frac{\sqrt{a - 1}}{a + \sqrt{a}}, \quad \text{при } a = 16. \]
- (3 балла) Из уравнения \[ \sqrt{\sqrt{\frac{1}{2} \sqrt{\frac{1}{2} \sqrt{\frac{1}{2}}}}} = 2^n \] найдите $n$.
- (2 балла) В параллелограмме $ABCD$ биссектриса $AM$ делит его сторону $BC$ на отрезки $BM = 3$, $CM = 4$. Найдите периметр этого параллелограмма.
- (3 балла) В прямоугольнике $ABCD$ к диагонали $AC$ проведён перпендикуляр $BE$. $AE : EC = 1 : 3$, $AB = 12$. Найдите $AC$.
- (4 балла) В прямоугольном треугольнике $ABC$ $(\angle C = 90^\circ)$, $AB = 10$, проведена медиана $BM = \sqrt{73}$. Найдите площадь треугольника $ABC$.
- (5 баллов) В равнобедренной трапеции $ABCD$, $AD \parallel BC$, $AB = BC = CD$. Высота $BM$ пересекает диагональ $AC$ в точке $K$. $BK = 5$, $KM = 4$. Найдите периметр трапеции $ABCD$.
- (5 баллов) В прямоугольной трапеции $ABCD$, $AD \parallel BC$, $\angle A = 90^\circ$. $O$ – центр вписанной в неё окружности. $OC = 15$, $OD = 20$. Найдите площадь трапеции $ABCD$.
Материалы школы Юайти
youit.school ©
Решения задач
- Найдите 65% от 125.
Решение: Чтобы найти 65% от числа 125, умножим 125 на 0,65:
\( 0,65 \times 125 = 81,25 \)
Ответ: 81,25.
- 45% от числа равны 99. Найдите это число.
Решение: Пусть искомое число равно \( x \). Тогда:
\( 0,45x = 99 \)
\( x = \frac{99}{0,45} = 220 \)
Ответ: 220.
- Вычислить
\[
\frac{7}{15} : \left(2 \cdot 0{,}4 - 4 \cdot \frac{1}{3} \right)
\]
Решение: Вычислим выражение в скобках:
\( 2 \cdot 0,4 = 0,8 \)
\( 4 \cdot \frac{1}{3} = \frac{4}{3} \)
\( 0,8 - \frac{4}{3} = \frac{12}{15} - \frac{20}{15} = -\frac{8}{15} \)
Тогда деление:
\( \frac{7}{15} : \left( -\frac{8}{15} \right) = \frac{7}{15} \times \left( -\frac{15}{8} \right) = -\frac{7}{8} \)
Ответ: \( -\frac{7}{8} \).
- Решить уравнение
\[
\frac{x^2}{x^2 - 2x + 1} - \frac{2x}{x - 1} = 3.
\]
Если корней несколько, то в ответ запишите их сумму.
Решение: Преобразуем уравнение, разложив знаменатель:
\( \frac{x^2}{(x-1)^2} - \frac{2x}{x-1} = 3 \)
Введём замену \( t = \frac{x}{x-1} \). Тогда уравнение примет вид:
\( t^2 - 2t - 3 = 0 \)
Корни: \( t_1 = 3 \), \( t_2 = -1 \)
Для \( t = 3 \):
\( \frac{x}{x-1} = 3 \Rightarrow x = \frac{3}{2} \)
Для \( t = -1 \):
\( \frac{x}{x-1} = -1 \Rightarrow x = \frac{1}{2} \)
Сумма корней: \( \frac{3}{2} + \frac{1}{2} = 2 \)
Ответ: 2.
- При каких \( m \) уравнение
\[
m = -2 - \frac{x + 4}{x^2 + 4x}
\]
не имеет решения. В ответ записать сумму значений параметра \( m \).
Решение: Преобразуем уравнение:
\( m + 2 = -\frac{x + 4}{x(x+4)} \)
При \( x \neq -4, 0 \) получаем \( x = -\frac{1}{m + 2} \)
Исключая \( x = -4 \), находим \( m = -\frac{7}{4} \). При \( m = -2 \) уравнение не имеет решений.
Сумма значений: \( -\frac{7}{4} - 2 = -\frac{15}{4} \)
Ответ: \( -\frac{15}{4} \).
- Задан график квадратичной функции \( y = ax^2 + bx + c \). Найдите коэффициенты \( a \), \( b \), \( c \).
Решение: По графику определяем:
- Точка пересечения с осью OY: \( (0, 3) \) → \( c = 3 \)
- Вершина в точке \( (1, 1) \): \( -\frac{b}{2a} = 1 \Rightarrow b = -2a \)
- Подстановка вершины: \( 1 = a(1)^2 + (-2a)(1) + 3 \Rightarrow a = 2 \), \( b = -4 \)
Ответ: \( a = 2 \), \( b = -4 \), \( c = 3 \).
- Решите неравенство \( (x - 4)^2(1 - x)(x + 2) \geq 0 \). В ответ запишите сумму всех его целых решений.
Решение: Метод интервалов. Нули: \( x = 4 \) (кратность 2), \( x = 1 \), \( x = -2 \)
Решение неравенства: \( [-2, 1] \cup \{4\} \)
Целые решения: \( -2, -1, 0, 1, 4 \). Сумма: \( 2 \)
Ответ: 2.
- Постройте график неравенства \( 2|x| + 3|y| \leq 6 \) и найдите площадь получившейся фигуры.
Решение: Фигура — ромб с вершинами \( (\pm3, 0) \), \( (0, \pm2) \). Площадь:
\( 4 \times \left( \frac{1}{2} \times 3 \times 2 \right) = 12 \)
Ответ: 12.
- Решите систему уравнений:
\[
\begin{cases}
x + y - 4z = 1 \\
x + 2y - 3z = 5 \\
3x - 2y + 4z = 4
\end{cases}
\]
Решение: Вычитаем первое уравнение из второго:
\( y + z = 4 \) → \( y = 4 - z \)
Подставляем \( y = 4 - z \) в третье уравнение и решаем:
\( x = 2 \), \( y = 3 \), \( z = 1 \)
Ответ: \( (2, 3, 1) \).
- Вычислите:
\[
\left( \frac{\sqrt{a + 1}}{\sqrt{a - 1}} - \frac{4 \sqrt{a}}{a - 1} \right) : \frac{\sqrt{a - 1}}{a + \sqrt{a}}, \quad \text{при } a = 16.
\]
Решение: Подстановка \( a = 16 \):
\( \frac{\sqrt{17}}{\sqrt{15}} - \frac{16}{15} \)
Упрощаем и получаем ответ:
Ответ: 4.
- Из уравнения
\[
\sqrt{\sqrt{\frac{1}{2} \sqrt{\frac{1}{2} \sqrt{\frac{1}{2}}}}} = 2^n
\]
найдите \( n \).
Решение: Последовательно преобразуем левую часть:
\( 2^{-\frac{7}{16}} = 2^n \) → \( n = -\frac{7}{16} \)
Ответ: \( -\frac{7}{16} \).
- В параллелограмме \( ABCD \) биссектриса \( AM \) делит \( BC \) на \( BM = 3 \), \( CM = 4 \). Периметр равен \( 2(AB + BC) = 2(7 + 7) = 28 \)
Ответ: 28.
- В прямоугольнике \( ABCD \) \( AC = 24 \)
Ответ: 24.
- В прямоугольном треугольнике \( ABC \) площадь равна 24.
Ответ: 24.
- Периметр трапеции \( ABCD \) равен 66.
Ответ: 66.
- Площадь трапеции \( ABCD \) равна 300.
Ответ: 300.
Материалы школы Юайти