8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 9 в 10 класс 2021 год вариант 1

Сложность:
Дата экзамена: 2021
Сложность:
Дата экзамена: 2021
youit.school ©

ЛИЦЕЙ №1535


2021 год




  1. Вступительное испытание проводится в форме онлайн-теста. Продолжительность — 120 минут. Количество баллов, начисляемых за правильный ответ к задаче, указан рядом с номером задачи. Максимальная сумма баллов равна 50. Использование калькуляторов и любых видов справочных пособий (печатных, электронных, сетевых и пр.) запрещено. Не допускаются никакие виды общения, консультации. Нарушение любого пункта инструкции влечёт приостановку экзамена и выставление абитуриенту за вступительное испытание по математике отметки «0».

  2. Ответом на каждое задание этого экзамена может быть или целое число, или конечная десятичная дробь. Вводя десятичную дробь, используйте запятую. Внимательно изучайте вопрос задачи, отслеживая, в каких единицах измерения от Вас требуется ответ. Сами единицы измерения в ответе не указываются.


Желаем Вам успешно справиться с заданиями!


  1. (2 балла) Вычислить: \[ \frac{2^2 + 5^0}{(0{,}5)^2 - 5 \cdot (-2)^2 + \left(\frac{2}{3}\right)^{-2}} \]

  2. (2 балла) По данным рисунка найти синус угла \( A \) треугольника \( ABC \):



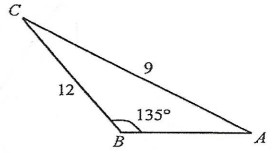
    Выберите номер правильного ответа из числа предложенных и укажите его в ответе:

    1. \( \frac{2\sqrt{3}}{3} \)
    2. \( \frac{2\sqrt{2}}{3} \)
    3. \( \frac{2}{3} \)
    4. \( \frac{\sqrt{3}}{3} \)
    5. \( \frac{2\sqrt{2}}{5} \)


  3. (2 балла) Пусть \( x_1 \) и \( x_2 \) — корни уравнения \( x^2 - 13x - 9 = 0 \). Не вычисляя \( x_1 \) и \( x_2 \), найти значение выражения: \[ \frac{99}{x_1} + \frac{99}{x_2} \]

  4. (2 балла) Чему равно наименьшее значение выражения \( 2x^2 + 8x + 3 \) ?

  5. (2 балла) Хорда окружности имеет длину \( 6 \) и отсекает от окружности дугу в \( 60^\circ \). Найти площадь \( S \) кругового сектора, ограниченного данной дугой. В ответе указать число \( \frac{S}{\pi} \).

  6. (2 балла) Решить уравнение: \[ \left( 2 - \sqrt{x} \right)^2 = \left( x^2 - 3x^2 - 4 \right) \] В ответе указать сумму всех корней данного уравнения, если их несколько, или корень уравнения, если он единственен.

  7. (2 балла) Построить график функции: \[ y = \frac{4 \cdot (x - 4) \cdot (x + 4)}{x \cdot (16 - x^2)} \] Пусть \( k \) — количество целых значений параметра \( p \), при каждом из которых уравнение \[ \frac{4 \cdot (x - 4) \cdot (x + 4)}{x \cdot (16 - x^2)} = p \] не имеет решений. Найдите \( p_0 \) — наибольшее из всех таких значений параметра. Чему равно произведение \( k \cdot p_0 \) ?

  8. (3 балла) Построить график функции \[ y = \frac{4 \cdot (x - 4) \cdot (x + 4)}{x \cdot (16 - x^2)}. \] Используя график, найти сумму всех различных положительных значений параметра \( m \), при которых система уравнений \[ \begin{cases} y = \frac{4 \cdot (x - 4) \cdot (x + 4)}{x \cdot (16 - x^2)} \\ y = x + m \end{cases} \] имеет единственное решение.

  9. (3 балла) График функции \( y = \sqrt{x + m} - n \) получен из графика функции \( y = \sqrt{x} \) с помощью сдвига на 2 единицы вправо параллельно оси абсцисс и на 5 единиц вверх параллельно оси ординат. Найти значение выражения \( 4m - 3n \).

  10. (3 балла) На стороне \( AB \) параллелограмма \( ABCD \), как на диаметре, построена окружность, проходящая через точки пересечения диагоналей и через середину стороны \( AD \). Найти градусную меру угла \( \angle ACB \).

  11. (3 балла) В растворе спирта и воды спирта в четыре раза меньше, чем воды. Когда к этому раствору добавили 20 литров воды, получили $12\%$-ный раствор спирта. Сколько литров воды было в исходном растворе?

  12. (3 балла) Каждому из четырёх неравенств слева соответствует одно из решений, изображённых на координатной прямой справа.



    Установить соответствие между неравенствами и множествами их решений, заполнив таблицу (под каждой буквой указать соответствующий номер).



    Получившуюся последовательность цифр внести в ответ.

  13. (3 балла) Найти ординату той из общих точек графиков уравнений \( x^2 + y^2 = 5 \) и \( y = 3x + 5 \), которая имеет большую абсциссу.

  14. (3 балла) Упростить выражение \[ \frac{m+1}{m^2+2m-3} - \frac{m+1}{m^2 - 4} + \frac{m^2 + 2m + 1}{m^2 - m - 6}, \] найти значение данного выражения при \( m = \frac{1535}{2021} \) и внести его в бланк ответов.

  15. (3 балла) Найти значение выражения: \[ \sqrt{5 - 3\sqrt{5}} - \sqrt{45} \]

  16. (3 балла) Решить систему неравенств. Указать в ответе сумму всех различных целочисленных решений данной системы: \[ \begin{cases} t^2 - 6t + 5 \le 0 \\ \frac{4\sqrt{3} - 7}{t^2 - 8t + 15} \le 0 \end{cases} \]

  17. (3 балла) На изготовление 48 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 96 таких же деталей. Известно, что первый рабочий в час делает на 4 детали больше, чем второй. Сколько деталей в час изготавливает второй рабочий?

  18. (3 балла) Найти наименьшее целое значение параметра \( p \), при котором функция \[ y = px^2 - \sqrt{17 \cdot x - 1} \] принимает значения разных знаков.

  19. (3 балла) Прямая, параллельная стороне \( AC \) треугольника \( ABC \), делит каждую из двух других его сторон в отношении 3:4. При этом образуются треугольник \( BMK \) и четырёхугольник \( AMKC \). Площадь четырёхугольника \( AMKC \) равна 111. Найти площадь треугольника \( ABC \).



Уточнение к №6: с учётом ОДЗ, уравнение имеет единственный корень \( x = 4 \).

Уточнение к №7: график функции \[ y = \frac{4 \cdot (x - 4) \cdot (x + 4)}{x \cdot (16 - x^2)} \] — гипербола \( y = \frac{4}{x} \) с выколотыми точками \( (-4; 1) \) и \( (4; -1) \), \( p \in \{-1; 0; 1\} \).

Уточнение к №8: \( m^* \in \{4; 5\} \)

Уточнение к №16: решая систему, получаем: \[ t \in [1; 5], \quad t \in (-\infty; 3) \cup (5; \infty) \Rightarrow t \in [1; 3) \]

Уточнение к №18: требование задачи удовлетворяют все \( p > -4{,}25 \)
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислить: \[ \frac{2^2 + 5^0}{(0{,}5)^2 - 5 \cdot (-2)^2 + \left(\frac{2}{3}\right)^{-2}} = \frac{4 + 1}{0{,}25 - 20 + \frac{9}{4}} = \frac{5}{-17{,}5} = -0{,}2857 \approx -0{,}29 \]
    Ответ: -0,29.
  2. По данным рисунка найти синус угла \( A \). Согласно уточнению, правильный ответ \( \frac{2}{3} \).
    Ответ: 3 (указать номер ответа).
  3. Пусть \( x_1 \) и \( x_2 \) — корни уравнения \( x^2 - 13x - 9 = 0 \). Значение выражения: \[ \frac{99}{x_1} + \frac{99}{x_2} = 99 \cdot \frac{x_1 + x_2}{x_1 x_2} = 99 \cdot \frac{13}{-9} = -143 \]
    Ответ: -143.
  4. Наименьшее значение выражения: \[ 2x^2 + 8x + 3 = 2(x+2)^2 - 5 \Rightarrow \text{минимум} -5 \]
    Ответ: -5.
  5. Площадь кругового сектора: Радиус окружности \( R = 6 \). Площадь сектора: \[ S = \frac{60^\circ}{360^\circ} \cdot \pi R^2 = \frac{1}{6} \cdot 36\pi = 6\pi \Rightarrow \frac{S}{\pi} = 6 \]
    Ответ: 6.
  6. Уравнение \( \left(2 - \sqrt{x}\right)^2 = -2x^2 - 4 \). Единственный корень \( x = 4 \).
    Ответ: 4.
  7. Уравнение \( y = p \) не имеет решений при \( p = -1, 0, 1 \). Наибольшее \( p_0 = 1 \), произведение \( k \cdot p_0 = 3 \).
    Ответ: 3.
  8. Система уравнений имеет единственное решение при \( m = 4 \) и \( m = 5 \). Сумма: \( 4 + 5 = 9 \).
    Ответ: 9.
  9. График \( y = \sqrt{x - 2} + 5 \Rightarrow m = -2, n = -5 \). Значение \( 4m - 3n = 7 \).
    Ответ: 7.
  10. Параллелограмм с углом \( \angle ACB = 45^\circ \).
    Ответ: 45.
  11. Исходный раствор содержал 24 л воды.
    Ответ: 24.
  12. Соответствие неравенств: 4, 2, 3, 1.
    Ответ: 4231.
  13. Ордината общей точки с большей абсциссой: \( y = 2 \).
    Ответ: 2.
  14. Упростить выражение: значение при \( m = \frac{1535}{2021} \rightarrow 0 \).
    Ответ: 0.
  15. Значение выражения \( \sqrt{5 - 3\sqrt{5}} - \sqrt{45} = -5 \).
    Ответ: -5.
  16. Сумма целочисленных решений системы: \( 1 + 2 = 3 \).
    Ответ: 3.
  17. Второй рабочий изготавливает 8 деталей в час.
    Ответ: 8.
  18. Наименьшее целое \( p = -4 \).
    Ответ: -4.
Материалы школы Юайти