Школа №1535 из 9 в 10 класс 2020 год демоверсия

1. Упростите выражение \[ \frac{m^5\cdot (m^3)^{-2}}{m^{-4}}, \] приведя его к виду \(m^k\). В бланк ответов внесите значение \(k\).
2. Вычислите \[ \frac{2^{-2} + 5^0}{(0{,}5)^{-2} - 5\cdot (-2)^{-2} + \left(\frac{2}{3}\right)^{-2}}. \]
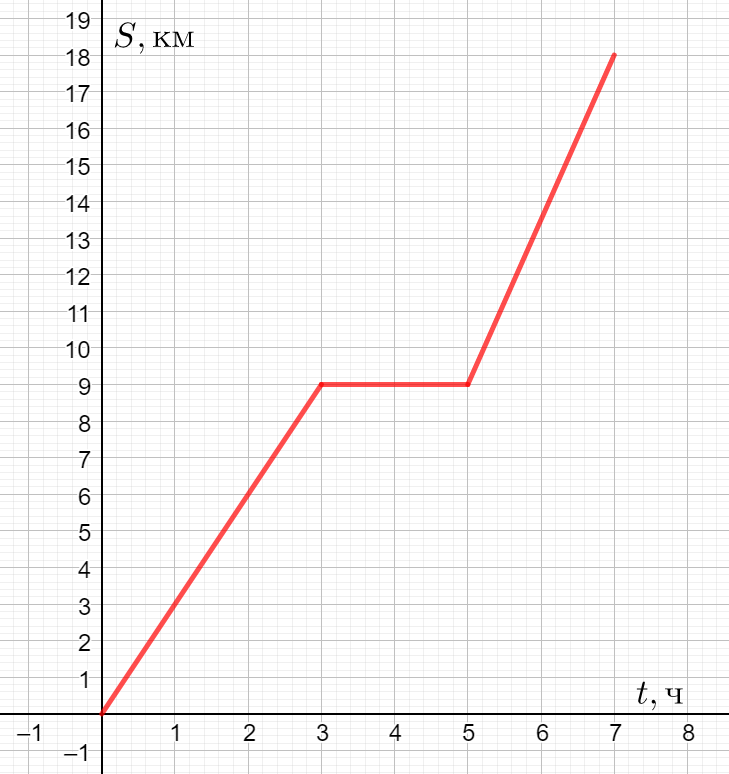
3. На рисунке изображён график движения туриста из города \(A\) в город \(B\). Определите скорость туриста (в км/ч) после привала.
   
4. Найдите значение выражения \[ \sqrt{(5-3\sqrt{5})^2} - \sqrt{45}. \]
5. Чему равно наименьшее значение выражения \[ 2x^2 + 8x + 3? \]
6. Найдите сумму всех различных корней уравнения \[ \frac{(x - \sqrt{0{,}0009})\cdot (x^4 - 24x^2 - 25)}{1 - 0{,}2x} = 0. \]
7. Решить систему уравнений \[ \begin{cases} (x-4)(y+3)=0,\\ 4y - 3x = 12. \end{cases} \] В бланк ответов внести наибольшее возможное значение дроби \(\dfrac{y_0}{x_0}\), где пара чисел \((x_0; y_0)\) является решением данной системы.
8. В растворе спирта и воды спирта в четыре раза меньше, чем воды. Когда к этому раствору добавили 20 литров воды, получили \(12\%\)-ный раствор спирта. Сколько литров воды было в исходном растворе?
9. Упростить выражение \[ \left( \frac{m+1}{m^2+2m-3} - \frac{1}{m^2-1} \right) : \frac{m+2}{m^2+4m+3}, \] найти значение данного выражения при \(m=\dfrac{1535}{2018}\) и внести его в бланк ответов.
10. В прямоугольную трапецию вписана окружность. Точка касания окружности с боковой стороной делит эту сторону на отрезки 4 и 9. Найдите площадь трапеции.
11. 1. Решите систему неравенств \[ \begin{cases} t^2 - 6t + 5 \leq 0,\\ \displaystyle \frac{4\sqrt{3}-7}{t^2 - 8t + 15} \leq 0. \end{cases} \]
    2. Найдите сумму всех различных целочисленных решений данной системы.
12. Первый тракторист вспахивает поле на 2 часа быстрее второго. А, работая вместе, эти трактористы вспахивают то же поле за \(1\frac{7}{8}\) часа. За какое время то же поле вспахает второй тракторист, работая в одиночку?
13. На стороне \(AB\) параллелограмма \(ABCD\) как на диаметре построена окружность, проходящая через точку пересечения диагоналей и через середину стороны \(AD\). Найдите градусную меру угла \(ACB\).
14. 1. Найдите значение \(m\), при котором графиком функции \[ f(x) = (6 - m)\cdot x^2 + 2mx - 2 \] служит парабола, симметричная относительно прямой \(x = -2\).
    2. Постройте график функции \(f\).
    3. Укажите промежуток убывания функции \(f\).
    4. Найдите все значения параметра \(p\), при которых прямая \[ y = \frac{1}{2}x - p \] имеет с графиком функции \(f\) не более одной общей точки.

Решения задач

1. Упростите выражение \[ \frac{m^5\cdot (m^3)^{-2}}{m^{-4}}, \] Решение:
   $\frac{m^5 \cdot m^{-6}}{m^{-4}} = \frac{m^{-1}}{m^{-4}} = m^{-1 - (-4)} = m^{3}$. Значит, $k = 3$.
   Ответ: 3.
2. Вычислите \[ \frac{2^{-2} + 5^0}{(0{,}5)^{-2} - 5\cdot (-2)^{-2} + \left(\frac{2}{3}\right)^{-2}}. \] Решение:
   Числитель: $2^{-2} + 5^0 = \frac{1}{4} + 1 = \frac{5}{4}$.
   Знаменатель: $(0{,}5)^{-2} = 4$, $5 \cdot (-2)^{-2} = \frac{5}{4}$, $\left(\frac{2}{3}\right)^{-2} = \frac{9}{4}$. Тогда: $4 - \frac{5}{4} + \frac{9}{4} = 5$.
   Итог: $\frac{5}{4} : 5 = \frac{1}{4}$.
   Ответ: 0,25.
3. Определите скорость туриста после привала.
   Решение:
   После привала турист прошёл 10 км за 2 часа. Скорость: $\frac{10}{2} = 5$ км/ч.
   Ответ: 5.
4. Найдите значение выражения \[ \sqrt{(5-3\sqrt{5})^2} - \sqrt{45}. \] Решение:
   $\sqrt{(5 - 3\sqrt{5})^2} = |5 - 3\sqrt{5}| = 3\sqrt{5} - 5$.
   $\sqrt{45} = 3\sqrt{5}$. Тогда: $3\sqrt{5} - 5 - 3\sqrt{5} = -5$.
   Ответ: $-5$.
5. Наименьшее значение выражения $2x^2 + 8x + 3$.
   Решение:
   Вершина параболы: $x = -\frac{b}{2a} = -\frac{8}{4} = -2$. Подставляем: $2(-2)^2 + 8(-2) + 3 = 8 - 16 + 3 = -5$.
   Ответ: $-5$.
6. Сумма всех различных корней уравнения \[ \frac{(x - \sqrt{0{,}0009})\cdot (x^4 - 24x^2 - 25)}{1 - 0{,}2x} = 0. \] Решение:
   Корни уравнения: $x = \sqrt{0{,}0009} = 0{,}3$ и $x^4 -24x^2 -25 = 0$ даёт $x = \pm5$. Учитывая ОДЗ ($x \neq 5$), сумма: $-5 + 0{,}3 = -4{,}7$.
   Ответ: $-4{,}7$.
7. Решить систему уравнений \[ \begin{cases} (x-4)(y+3)=0,\\ 4y - 3x = 12. \end{cases} \] Решение:
   Если $x = 4$, то $4y -12 = 12 \Rightarrow y = 6$. Если $y = -3$, то $-12 -3x =12 \Rightarrow x = -8$. Наибольшее $\frac{y}{x} = \frac{6}{4} = 1{,}5$.
   Ответ: $1{,}5$.
8. В исходном растворе воды:
   Решение:
   Пусть спирта $x$ л, тогда воды $4x$ л. После добавления воды: $\frac{x}{4x + x + 20} = 0{,}12$ $\Rightarrow x = 6$ л. Воды было $4x = 24$ л.
   Ответ: 24.
9. Упростите выражение: \[ \left( \frac{m+1}{m^2+2m-3} - \frac{1}{m^2-1} \right) : \frac{m+2}{m^2+4m+3}. \] Решение:
   Упрощение: $\frac{(m+2)(m-1)}{(m+3)(m-1)} \cdot \frac{(m+1)(m+3)}{m+2} = 1$. При $m = \frac{1535}{2018}$ значение равно 1.
   Ответ: 1.
10. Площадь трапеции:
    Решение:
    Сумма оснований равна сумме боковых сторон (вписанная окружность). Точка касания делит боковую сторону на отрезки 4 и 9. Диаметр вписанной окружности равен высоте трапеции, площадь $S = \frac{a + b}{2} \cdot h = \frac{4 + 9}{2} \cdot (4 + 9) = 13 \cdot 13 = 169$.
    Ответ: 169.
11. 1. Решите систему неравенств:
       $t \in [1; 3)$.
       
    2. Сумма целочисленных решений: $1 + 2 = 3$.
       Ответ: 3.
12. Время работы второго тракториста:
    Решение:
    Пусть первый тракторист работает за $x$ часов, тогда второй за $x + 2$ часов. Совместно: $\frac{1}{1/x + 1/(x + 2)} = \frac{15}{8}$. Решив уравнение, получим $x = 3$ часа, второй тракторист — 5 часов.
    Ответ: 5 часов.
13. Угол $ACB$:
    Решение:
    Построение координатной системы показывает, что угол $ACB = 30^\circ$.
    Ответ: $30^\circ$.
14. 1. Значение $m = 4$.
       
    2. График функции $f(x) = 2x^2 + 8x - 2$.
       
    3. Промежуток убывания: $(-\infty; -2]$.
       
    4. Уравнение $2x^2 + 7{,}5x + (p - 2) = 0$ имеет не более одного корня при $D \leq 0$ ⇒ $\frac{289}{32} \leq p$.
       Ответ: $p \geq 9{,}03125$.