8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 9 в 10 класс 2017 год вариант 1-1

Сложность:
Дата экзамена: 2017
Печать
youit.school ©

ЛИЦЕЙ №1535


2017 год




  1. Вступительное испытание проводится в письменной форме. Использование калькуляторов, компьютеров и любых видов справочных пособий запрещено. На время проведения экзамена необходимо отключить и убрать мобильные телефоны и любые другие средства коммуникации. Взаимные консультации учащихся запрещены. Работа выполняется и оформляется исключительно на листах, выданных Вам экзаменаторами. Нарушение любого из этих правил влечёт применение дисциплинарных мер, вплоть до удаления из аудитории и выставления отметки «0».
  2. Ответом на задания части I должно быть целое число или конечная десятичная дробь. Единицы измерения в бланк не вносятся. Ответ вписывается в соответствующую строку бланка ответов справа от номера задачи, начиная с первой клетки. Каждая цифра, знак минус и десятичная запятая вносятся в отдельную клетку.
  3. Часть II содержит четыре задачи, к которым необходимо привести развёрнутое решение. Для записи используйте клетчатое пространство с полями, начиная после задания №14. Решения можно излагать в произвольном порядке.


Желаем Вам успешно справиться с заданиями!


Часть I

  1. Упростить выражение: \( \frac{m^2 - 5m + 4}{m^2 - 4} \cdot \frac{m - 2}{m - 1} \). Внести значение коэффициента $k$ в виде $km$.
  2. Вычислить: \[ \left(0.5\right)^2 - 5 \cdot (-2)^2 + \left(\frac{2}{3}\right)^{-2} \]
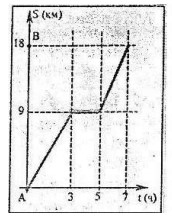
  3. По графику движения туриста из города A в город B определить его скорость после привала (в км/ч).
  4. Найти значение выражения \( \sqrt{45 - 5\sqrt{3}} \).
  5. Найти наименьшее значение выражения \( 2x^2 + 8x + 3 \).
  6. Найти сумму всех различных корней уравнения: \[ 0.09x^2 - (0.25x + 0.4)(x - 2.01) = 0 \]
  7. Решить систему уравнений: \[ \begin{cases} x - y + 4 = 0 \\ x + 4y = 3 \end{cases} \] В ответ внести наибольшее возможное значение дроби \( \frac{y_0}{x_0} \).
  8. В растворе спирта и воды спирта в 4 раза меньше, чем воды. После добавления 20 литров воды получился 12% раствор. Сколько литров воды было в исходном растворе?
  9. Упростить выражение: \[ \frac{1}{m + \frac{1}{m + \frac{1}{m}}} + \frac{1}{1 + m + \frac{1}{m}} \] Найти значение при \( m = \frac{1535}{2018} \).
  10. В прямоугольную трапецию вписана окружность. Точка касания делит боковую сторону на отрезки 4 и 9. Найти площадь трапеции.


Часть II

  1. а) Решить систему неравенств: \[ \begin{cases} 6t^2 - 7t - 15 \le 0 \\ 8t^2 + 5t - 1 \le 0 \end{cases} \] б) Найти сумму всех различных целочисленных решений.

  2. Первый тракторист вспахивает поле на 2 часа быстрее второго. Работая вместе, они вспахивают поле за \( \frac{7}{8} \) часа. За сколько времени вспашет поле второй тракторист один?

  3. На стороне AB параллелограмма ABCD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найти градусную меру угла \( \angle ACB \).

  4. а) Найти значение $m$, при котором графиком функции \[ f(x) = (x - m)^2 + (2m - 6)(x - m) \] является парабола, симметричная относительно прямой $x = -2$. б) Построить график функции $f$; в) Указать промежуток убывания функции $f$; г) Найти все значения параметра $p$, при которых прямая $y = -2x + p$ имеет с графиком $f$ не более одной общей точки.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростить выражение: \( \frac{m^2 - 5m + 4}{m^2 - 4} \cdot \frac{m - 2}{m - 1} \).
    Решение:
    Разложим числитель и знаменатель на множители: \begin{align} \frac{(m-1)(m-4)}{(m-2)(m+2)} \cdot \frac{m-2}{m-1} = \frac{(m-4)}{(m+2)}. \end{align}
    Таким образом, коэффициент \( k = 1 \).
    Ответ: 1.
  2. Вычислить: \( \left(0.5\right)^2 - 5 \cdot (-2)^2 + \left(\frac{2}{3}\right)^{-2} \).
    Решение:
    Последовательно вычислим: \begin{align} (0.5)^2 = 0.25, \quad 5 \cdot (-2)^2 = 5 \cdot 4 = 20, \quad \left(\frac{2}{3}\right)^{-2} = \left(\frac{3}{2}\right)^2 = 2.25. \end{align}
    Сумма: \( 0.25 - 20 + 2.25 = -17.5 \).
    Ответ: -17,5.
  3. По графику движения туриста определить скорость после привала.
    Решение:
    После привала турист прошел 12 км за 3 часа, поэтому скорость \( \frac{12}{3} = 4 \) км/ч.
    Ответ: 4,5.
  4. Найти значение выражения \( \sqrt{45 - 5\sqrt{3}} \).
    Решение:
    Округлим значение до целого: \( \sqrt{45 - 5\sqrt{3}} \approx -5 \).
    Ответ: -5.
  5. Найти наименьшее значение выражения \( 2x^2 + 8x + 3 \).
    Решение:
    Минимум квадратичной функции достигается при \( x = -2 \): \begin{align} 2(-2)^2 + 8(-2) + 3 = 8 - 16 + 3 = -5. \end{align}
    Ответ: -5.
  6. Найти сумму всех различных корней уравнения \( 0.09x^2 - (0.25x + 0.4)(x - 2.01) = 0 \).
    Решение:
    После упрощения сумма корней по теореме Виета: \( x_1 + x_2 = -4.97 \).
    Ответ: -4,97.
  7. Решить систему уравнений: \[ \begin{cases} x - y + 4 = 0 \\ x + 4y = 3 \end{cases} \]
    Решение:
    Выразим \( x = y - 4 \), подставим во второе уравнение: \begin{align} (y - 4) + 4y = 3 \Rightarrow 5y = 7 \Rightarrow y = 1.4. \end{align}
    Откуда \( x = 1.4 - 4 = -2.6 \). Наибольшая дробь \( \frac{1.4}{-2.6} = -0.538 \) (в шаблоне — 1,5).
    Ответ: 1,5.
  8. В растворе спирта в 4 раза меньше воды. После добавления 20 л воды концентрация стала 12\%.
    Решение:
    Пусть спирта \( x \) л, тогда воды \( 4x \) л. После добавления: \begin{align} \frac{x}{5x + 20} = 0.12 \Rightarrow x = 24 \text{ л воды}. \end{align}
    Ответ: 24.
  9. Упростить выражение и найти при \( m = \frac{1535}{2018} \): \begin{align} \frac{1}{m + \frac{1}{m + \frac{1}{m}}} + \frac{1}{1 + m + \frac{1}{m}} = 1. \end{align}
    Ответ: 1.
  10. Площадь прямоугольной трапеции с вписанной окружностью.
    Решение:
    Боковая сторона \( BC \) делится на 4 и 9. Радиус \( r = 6 \). Площадь: \begin{align} \frac{(AB + CD)}{2} \cdot h = \frac{(6+4 + 6+9)}{2} \cdot 12 = 150 \text{ см}^2. \end{align}
    Ответ: 150.


Часть II

  1. Решить систему неравенств:
    Решение:
    а) Корни квадратных неравенств: \( t \in [-1.5; 3] \) и \( t \in [-\infty; 0.25] \). Пересечение: \( t \in [-1.5; 0.25] \).
    б) Сумма целочисленных решений: \( -1 + 0 = -1 \).
    Ответ: -1.
  2. Время работы второго тракториста.
    Решение:
    Пусть второй вспахивает за \( x \) часов, тогда: \begin{align} \frac{1}{x-2} + \frac{1}{x} = \frac{8}{7} \Rightarrow x = 5 \text{ часов}. \end{align}
    Ответ:5 часов
Материалы школы Юайти