Школа №1535 из 9 в 10 класс 2015 год демоверсия

ЛИЦЕЙ №1535

2017 год

Демовариант

1. Запишите десятичную дробь, равную сумме \[ 6\cdot10^{-1} + 5\cdot10^{-3} + 3\cdot10^{-4}. \]
2. Найдите значение выражения \[ 1.4 + \frac{3\cdot7.8}{2.5}. \]
3. Решите неравенство \[ 5 + \frac{4x-3}{2} > 5x + \frac12. \] В ответе запишите наибольшее целое решение неравенства.
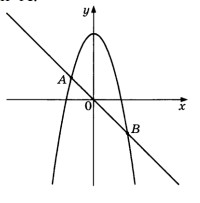
4. На рисунке изображены графики функций \(y=-x^2+6\) и \(y=-x\). Вычислите координаты точки \(A\), лежащей на их пересечении. В ответе запишите ординату точки \(A\).
   
5. Найдите корни уравнения \((x+8)^2 = (x+3)^2\). В ответе запишите сумму квадратов корней.
6. Геометрическая прогрессия задана условиями \(b_1=5\), \(b_{n+1}=3b_n\). Найдите сумму первых четырёх членов.
7. Решите неравенство \[ 4x^2 + 10x -20 \le (x+2)^2. \] В ответе запишите сумму всех целых решений неравенства.
8. Упростите выражение \[ \Bigl(\frac{a - b}{a} - \frac{a + b}{b}\Bigr) :\Bigl(\frac{1}{a^2} + \frac{1}{b^2}\Bigr), \] и найдите его значение при \(a=\sqrt7-2\), \(b=\sqrt7+2\).
9. Сократите дробь \(\displaystyle \frac{2^2\cdot4^8}{16^5\cdot5^2}\).
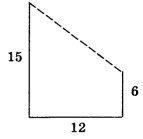
10. В 12 м одна от другой растут две сосны. Высота первой — 15 м, второй — 6 м. Найдите расстояние (в метрах) между их вершинами.
    
11. Решите систему неравенств: \[ \begin{cases} (x + 2)\,(2 - x) < (x + 3)\,(4 - x),\\[6pt] \dfrac{5 + x}{4} - \dfrac{2x - 1}{6} \;\ge\; 1. \end{cases} \]
12. На изготовление 40 деталей первый рабочий тратит на два часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на одну деталь больше?
13. 1. Постройте график функции \[ y = \frac{2x + 1}{2x^2 + x}. \]
    2. В той же системе координат постройте график функции \(y = x^2\).
    3. Используя построенные графики, решите систему уравнений: \[ \begin{cases} y = \dfrac{2x + 1}{2x^2 + x},\\ y = x^2. \end{cases} \]
    4. Определите, при каких значениях \(k\) прямая \(y = kx\) имеет с графиком \(\displaystyle y = \frac{2x + 1}{2x^2 + x}\) ровно одну общую точку.

Решения задач

1. Запишите десятичную дробь, равную сумме \[ 6\cdot10^{-1} + 5\cdot10^{-3} + 3\cdot10^{-4}. \]
   Решение: Преобразуем каждое слагаемое в десятичную дробь:
   $6\cdot10^{-1} = 0,6$;
   $5\cdot10^{-3} = 0,005$;
   $3\cdot10^{-4} = 0,0003$.
   Сумма: $0,6 + 0,005 + 0,0003 = 0,6053$.
   Ответ: 0,6053.
   
   
2. Найдите значение выражения \[ 1.4 + \frac{3\cdot7.8}{2.5}. \]
   Решение: Вычисляем последовательно:
   $3 \cdot 7,8 = 23,4$;
   $\frac{23,4}{2,5} = 9,36$;
   $1,4 + 9,36 = 10,76$.
   Ответ: 10,76.
   
   
3. Решите неравенство \[ 5 + \frac{4x-3}{2} > 5x + \frac12. \] В ответе запишите наибольшее целое решение неравенства.
   Решение: Умножаем обе части на 2 для упрощения:
   $10 + 4x - 3 > 10x + 1$;
   $7 + 4x > 10x + 1$;
   $-6x > -6$;
   $x < 1$.
   Наибольшее целое решение: 0.
   Ответ: 0.
   
   
4. На рисунке изображены графики функций \(y=-x^2+6\) и \(y=-x\). Вычислите координаты точки \(A\), лежащей на их пересечении. В ответе запишите ординату точки \(A\).
   Решение: Приравниваем функции: $-x^2 + 6 = -x$;
   $-x^2 + x + 6 = 0$;
   Корни: $x_1 = -2$, $x_2 = 3$.
   Ординаты точек: $y(-2) = 2$, $y(3) = -3$.
   Ответ: 2.
   
   
5. Найдите корни уравнения \((x+8)^2 = (x+3)^2\). В ответе запишите сумму квадратов корней.
   Решение:
   $(x+8)^2 - (x+3)^2 = 0$;
   $(x+8 - x -3)(x+8 + x +3) = 0$;
   $5(2x + 11) = 0$;
   $x = -5,5$.
   Сумма квадратов: $(-5,5)^2 = 30,25$.
   Ответ: 30,25.
   
   
6. Геометрическая прогрессия задана условиями \(b_1=5\), \(b_{n+1}=3b_n\). Найдите сумму первых четырёх членов.
   Решение: Знаменатель прогрессии $q = 3$;
   $b_1 = 5$, $b_2 = 15$, $b_3 = 45$, $b_4 = 135$.
   Сумма: $5 + 15 + 45 + 135 = 200$.
   Ответ: 200.
   
   
7. Решите неравенство \[ 4x^2 + 10x -20 \le (x+2)^2. \] В ответе запишите сумму всех целых решений неравенства.
   Решение: Преобразуем неравенство:
   $4x^2 +10x -20 \le x^2 +4x +4$;
   $3x^2 +6x -24 \le 0$;
   $x^2 +2x -8 \le 0$;
   Корни квадратного уравнения: $x = -4$, $x = 2$.
   Решение неравенства: $x \in [-4; 2]$.
   Целые решения: $-4, -3, -2, -1, 0, 1, 2$.
   Сумма: $-7$.
   Ответ: -7.
   
   
8. Упростите выражение \[ \Bigl(\frac{a - b}{a} - \frac{a + b}{b}\Bigr) :\Bigl(\frac{1}{a^2} + \frac{1}{b^2}\Bigr). \]
   Решение: Упрощаем числитель и знаменатель:
   Числитель: $\frac{a - b}{a} - \frac{a + b}{b} = -\frac{a^2 + b^2}{ab}$;
   Знаменатель: $\frac{1}{a^2} + \frac{1}{b^2} = \frac{b^2 + a^2}{a^2b^2}$;
   Результат деления: $-ab$.
   Подставляя $a=\sqrt7 -2$, $b=\sqrt7 +2$:
   $-(\sqrt7 -2)(\sqrt7 +2) = -3$.
   Ответ: -3.
   
   
9. Сократите дробь \(\displaystyle \frac{2^2\cdot4^8}{16^5\cdot5^2}\).
   Решение: Приводим степени к основанию 2:
   $\frac{2^2 \cdot (2^2)^8}{(2^4)^5 \cdot 5^2} = \frac{2^{18}}{2^{20} \cdot 25} = \frac{1}{2^2 \cdot 25} = \frac{1}{100}$.
   Ответ: $\frac{1}{100}$.
   
   
10. В 12 м одна от другой растут две сосны. Высота первой — 15 м, второй — 6 м. Найдите расстояние (в метрах) между их вершинами.
    Решение: Расстояние между вершинами — гипотенуза прямоугольного треугольника с катетами $(15-6)=9$ м и 12 м:
    $\sqrt{9^2 +12^2} = \sqrt{225} =15$ м.
    Ответ: 15.
    
    
11. Решите систему неравенств: \[ \begin{cases} (x + 2)\,(2 - x) < (x + 3)\,(4 - x),\\[6pt] \dfrac{5 + x}{4} - \dfrac{2x - 1}{6} \;\ge\; 1. \end{cases} \]
    Решение: Решаем первое неравенство:
    $(x + 2)(2 - x) = -x^2 +4$,
    $(x + 3)(4 - x) = -x^2 + x +12$;
    $-x^2 +4 < -x^2 +x +12$;
    $4 < x + 12$;
    $x > -8$.
    Решаем второе неравенство:
    $\frac{5 + x}{4} - \frac{2x -1}{6} \ge 1$;
    Умножаем на 12:
    $3(5 +x) -2(2x -1) \geq 12$;
    $15 +3x -4x +2 \geq 12$;
    $17 -x \geq 12$;
    $-x \geq -5$;
    $x \leq 5$.
    Решение системы: $x \in (-8; 5]$.
    Сумма целых решений: $-7 + (-6) + ... +5 = -13$.
    Ответ: -13.
    
    
12. На изготовление 40 деталей первый рабочий тратит на два часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на одну деталь больше?
    Решение: Пусть первый делает $x$ дет/час, тогда второй – $x +1$.
    Время первого: $\frac{40}{x}$ ч, время второго: $\frac{36}{x +1}$ ч.
    Уравнение: $\frac{40}{x} = \frac{36}{x +1} + 2$;
    Решая квадратное уравнение, получаем $x=5$.
    Ответ: 5.
    
    
13. 1. Постройте график функции \[ y = \frac{2x + 1}{2x^2 + x}. \]
       Решение: Функция упрощается до $y = \frac{1}{x}$ при $x \neq 0$, $x \neq -0,5$.
       
       
    2. В той же системе координат постройте график функции \(y = x^2\).
       
       
    3. Решите систему уравнений: \[ \begin{cases} y = \dfrac{2x + 1}{2x^2 + x},\\ y = x^2. \end{cases} \]
       Решение: Подставляем $y = x^2$ в первое уравнение:
       $x^2 = \frac{1}{x}$;
       $x^3 = 1$;
       $x = 1$, $y =1$.
       Ответ: $(1;1)$.
       
       
    4. Определите, при каких значениях \(k\) прямая \(y = kx\) имеет с графиком \(\displaystyle y = \frac{2x + 1}{2x^2 + x}\) ровно одну общую точку.
       Решение: Решаем уравнение $kx = \frac{1}{x}$ при условии $x \neq -0,5$.
       $kx^2 =1$;
       Единственное решение при $k=0$ (нет решений) или при $k=4$, когда одно решение пересекает выколотую точку.
       Ответ: $k=4$.