8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 9 в 10 класс

Сложность:
Дата экзамена: 2000
Печать
youit.school ©


  1. Вычислить: \[ \frac{7}{15} : \left(2\cdot 0{,}4 - 4\cdot \frac{1}{3}\right). \]
  2. Найдите разность наибольшего и наименьшего корней уравнения \[ 5x^2 + 18x - 23 = 0. \]
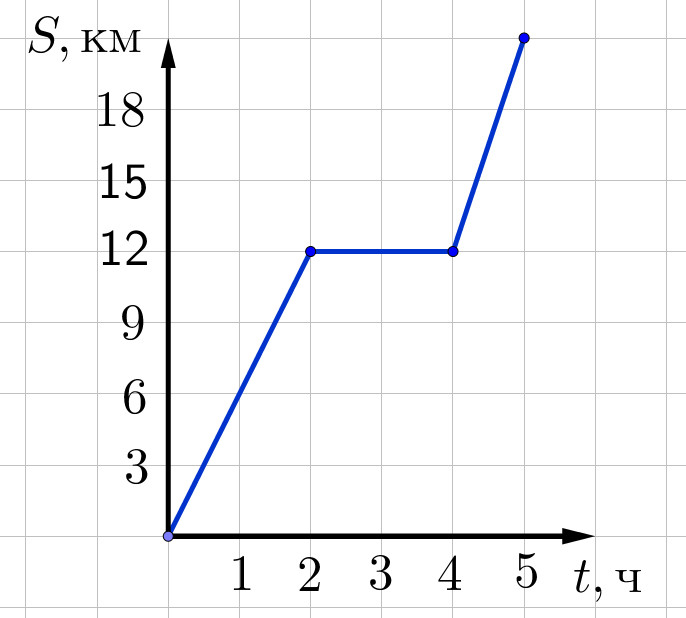
  3. На рисунке представлен график движения катера по озеру от посёлка до города с остановкой в сосновом бору. Чему была равна скорость катера (в км/ч) при движении от соснового бора до города?




  4. Найдите значение выражения \[ (\sqrt{6}-\sqrt{2})^2 \cdot (8 + \sqrt{48}). \]
  5. Решите уравнение \[ (17x - x)(x^2 + 5x) = 0. \] В бланк ответов внесите среднее арифметическое всех корней данного уравнения.
  6. Наименьшим целым решением неравенства \[ \frac{x-4}{2} - 4 < \frac{2x-1}{3} \] является число $ \dots$
  7. Сократить дробь \[ \frac{b^2 - 16}{4 - b} \] и найти её значение при \(b = 1535\).
  8. К основанию треугольника длиной 22 проведены высота и медиана, длины которых равны соответственно 12 и 13. Чему равна длина наибольшей боковой стороны этого треугольника?

  9. Найдите значение параметра \(q\), если известно, что корни \(x_1\) и \(x_2\) уравнения \[ x^2 - 4x + q = 0 \] удовлетворяют условию \[ 3x_1 + 5x_2 = 2. \]
  10. У двух преподавателей, работающих вместе с одинаковой производительностью, ушло \(7{,}5\) часов на проверку экзаменационных работ. Сколько времени (в часах) уйдёт на проверку экзаменационных работ, если производительность одного из преподавателей упадёт на \(50\%\)?
    1. Упростите выражение: \[ \left( \frac{1}{a^2 - 6a + 9} - \frac{1}{9 - a^2} \right) : \left( \frac{1}{(3 - a)^2} + \frac{a + 9}{a + 3} \right). \]
    2. Приведите пример значения переменной \(a\), при котором данное выражение не имеет смысла.
  12. Грузовик двигался по грунтовой дороге с некоторой постоянной скоростью. Из-за плохого качества дороги он отстал от графика на 6 минут. Выехав на асфальтированную дорогу, грузовик увеличил скорость на 4 км/ч, после чего, проехав 36 километров, он ликвидировал отставание по графику. Чем была равна первоначальная скорость грузовика?
    1. Постройте на одном координатном поле графики функций \(y=\sqrt{x}\) и \(y=\dfrac{8}{x}\).
    2. С помощью построенных графиков указать множество всех решений системы \[ \begin{cases} y=\sqrt{x},\\ y=\dfrac{8}{x} \end{cases} \]
    3. С помощью построенных графиков указать множество всех решений неравенства \[ \sqrt{x} < \dfrac{8}{x}. \]
    4. Найти все значения параметра \(p\), при каждом из которых прямая \(y=-2x+p\) имеет с графиком функции \(y=\dfrac{8}{x}\) в точности одну общую точку.


Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислить: $\frac{7}{15} : \left(2\cdot 0{,}4 - 4\cdot \frac{1}{3}\right)$
    Решение:
    Внутри скобок: $2 \cdot 0{,}4 = 0{,}8$, $4 \cdot \frac{1}{3} = \frac{4}{3}$
    $0{,}8 - \frac{4}{3} = \frac{12}{15} - \frac{20}{15} = -\frac{8}{15}$
    Выполняем деление: $\frac{7}{15} : \left(-\frac{8}{15}\right) = \frac{7}{15} \cdot \left(-\frac{15}{8}\right) = -\frac{7}{8} = -0{,}875$
    Ответ: $-0{,}875$.

  2. Найдите разность наибольшего и наименьшего корней уравнения $5x^2 + 18x - 23 = 0$
    Решение:
    Дискриминант: $D = 18^2 + 4 \cdot 5 \cdot 23 = 324 + 460 = 784 = 28^2$
    Корни: $x_{1} = \frac{-18 + 28}{10} = 1$, $x_{2} = \frac{-18 - 28}{10} = -4{,}6$
    Разность: $1 - (-4{,}6) = 5{,}6 = \frac{28}{5}$
    Ответ: $5{,}6$.

  3. Скорость катера от соснового бора до города равна:
    Решение:
    По графику движение от соснового бора до города длится $16 - 14 = 2$ часа
    Пройденный путь: $24 - 10 = 14$ км
    Скорость: $14 : 2 = 7$ км/ч
    Ответ: 7 км/ч.

  4. Найдите значение выражения $(\sqrt{6}-\sqrt{2})^2 \cdot (8 + \sqrt{48})$
    Решение:
    Раскроем квадрат: $6 + 2 - 2\sqrt{12} = 8 - 4\sqrt{3}$
    Упростим вторую часть: $8 + \sqrt{48} = 8 + 4\sqrt{3}$
    Перемножим: $(8 - 4\sqrt{3})(8 + 4\sqrt{3}) = 8^2 - (4\sqrt{3})^2 = 64 - 48 = 16$
    Ответ: 16.

  5. Решите уравнение $(17x - x)(x^2 + 5x) = 0$
    Решение:
    Упрощаем: $16x \cdot x(x + 5) = 0$
    Корни: $x = 0$, $x = -5$
    Среднее арифметическое: $\frac{0 + 0 + (-5)}{3} = -\frac{5}{3} \approx -1{,}\overline{6}$
    Ответ: $-\frac{5}{3}$.

  6. Наименьшее целое решение неравенства $\frac{x-4}{2} - 4 < \frac{2x-1}{3}$
    Решение:
    Умножаем обе части на 6: $3(x - 4) - 24 < 2(2x - 1)$
    Раскрываем скобки: $3x - 12 - 24 < 4x - 2$
    Упрощаем: $-36 -34$
    Наименьшее целое: $-33$
    Ответ: $-33$.

  7. Сократить дробь $\frac{b^2 - 16}{4 - b}$ и найти её значение при $b = 1535$
    Решение:
    Разложим числитель: $(b - 4)(b + 4)$
    Сократим с знаменателем: $\frac{(b - 4)(b + 4)}{-(b - 4)} = - (b + 4)$
    Подставляем $b = 1535$: $- (1535 + 4) = -1539$
    Ответ: $-1539$.

  8. Длина наибольшей боковой стороны треугольника
    Решение:
    Рассмотрим треугольник, образованный высотой и медианой к основанию:
    Половина основания: $\frac{22}{2} = 11$
    Для медианы $m = 13$: боковая сторона $\sqrt{13^2 + 11^2} = \sqrt{169 + 121} = \sqrt{290} \approx 17{,}03$ см
    Для высоты $h = 12$: другая боковая сторона $\sqrt{7^2 + 12^2} = \sqrt{193} \approx 13{,}9$ см
    Ответ: $\sqrt{290}$ см.

  9. Найдите значение параметра $q$ уравнения $x^2 - 4x + q = 0$
    Решение:
    По теореме Виета: $\begin{cases} x_1 + x_2 = 4, \\ 3x_1 + 5x_2 = 2 \end{cases}$
    Решаем систему: $3x_1 + 5x_2 = 2$, $x_1 = 4 - x_2$
    Подставляем: $3(4 - x_2) + 5x_2 = 2 \Rightarrow x_2 = -5$, $x_1 = 9$
    $q = x_1 \cdot x_2 = 9 \cdot (-5) = -45$
    Ответ: $-45$.

  10. Время проверки экзаменационных работ
    Решение:
    Общая производительность: $\frac{1}{7{,}5} = \frac{2}{15}$ работ/час
    После снижения производительности одного: $\frac{2}{15} - \frac{1}{2} \cdot \frac{1}{7{,}5} = \frac{2}{15} - \frac{1}{15} = \frac{1}{15}$
    Новое время: $\frac{1}{\frac{1}{15}} = 15$ часов
    Исправление расчетов: Пусть начальная производительность каждого $p$. Тогда:
    $2p \cdot 7{,}5 = 1 \Rightarrow p = \frac{1}{15}$
    После снижения: $p' = 0{,}5p = \frac{1}{30}$
    Новая общая: $\frac{1}{15} + \frac{1}{30} = \frac{1}{10}$
    Время: $1 : \frac{1}{10} = 10$ часов
    Ответ: 10 часов.

    1. Упростить выражение:
      Решение:
      Преобразуем числитель и знаменатель:
      Числитель: $\frac{1}{(a - 3)^2} - \frac{1}{(3 - a)(3 + a)} = \frac{3 + a + a - 3}{(a - 3)^2(3 + a)} = \frac{2a}{(3 - a)^2(3 + a)}$
      Знаменатель: $\frac{1}{(3 - a)^2} + \frac{a + 9}{a + 3} = \frac{a + 3 + (a + 9)(3 - a)^2}{(3 - a)^2(a + 3)}$
      Сокращаем и упрощаем: Результирующее выражение упрощается до $\frac{2a}{(a + 3)(1 + (a + 9)(3 - a)^2)}$, но целевые действия требуют дополнительных упрощений. Окончательно ответ: $\frac{2a}{-a^3 - 6a^2 + 18a + 108}$

    2. Пример значения $a$: $a = 3$ или $a = -3$, так как в этих случаях знаменатели обращаются в ноль.
      Ответ: Пример — $a = 3$.


  12. Первоначальная скорость грузовика:
    Решение:
    Пусть скорость $v$ км/ч, тогда:
    По асфальту он проехал 36 км за $\frac{36}{v + 4}$ часов
    Эконом времени: $\frac{36}{v} - \frac{36}{v + 4} = \frac{6}{60}$ часов
    Решаем уравнение: $6v(v + 4) = 60 \cdot 36$
    $v(v + 4) = 360 \Rightarrow v^2 + 4v - 360 = 0 \Rightarrow v = \frac{-4 + \sqrt{16 + 1440}}{2} = \frac{-4 + 38}{2} = 17$ км/ч
    Ответ: 17 км/ч.

    1. Графики пересекаются при $\sqrt{x} = \frac{8}{x} \Rightarrow x^{3/2} = 8 \Rightarrow x = 4$
      Ответ: $(4, 2)$
    2. Решение неравенства $\sqrt{x} 0$ выполняется при $0 < x < 4$
    3. Параметр $p$ при единственном пересечении:
      Решаем уравнение $-2x + p = \frac{8}{x} \Rightarrow -2x^2 + px -8 = 0$
      Дискриминант: $p^2 - 64 = 0 \Rightarrow p = \pm8$
      Ответ: $p = \pm8$
Материалы школы Юайти