8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 8 в 9 класс 2021 год вариант 1

Сложность:
Дата экзамена: 2021
Сложность:
Дата экзамена: 2021
youit.school ©

ЛИЦЕЙ №1535


2021 год




Время выполнения: 120 минут

Инструкция: Ответом на каждое из заданий может быть целое число, конечная десятичная дробь или выражение. Укажите только ответ без единиц измерения, если не сказано иное.

  1. (2 балла) Найдите 65% от 125.
  2. (2 балла) 45% от числа равны 99. Найдите это число.
  3. (2 балла) Вычислите: $ -3 \dfrac{1}{4} - 2 \dfrac{3}{5} + 4 \dfrac{3}{20} $.
  4. (3 балла) Вычислите: \[ (\sqrt{2} - 3)\sqrt{5} + 6\sqrt{3 + 2\sqrt{2}} - 7 \]
  5. (3 балла) Упростите выражение: \[ \dfrac{2^{n+2} + 2^{n-2}}{2^n} \]
  6. (2 балла) Решите уравнение: \[ \dfrac{x^2}{x^2 - 2x + 1} - \dfrac{2x}{x - 1} = 3 \]
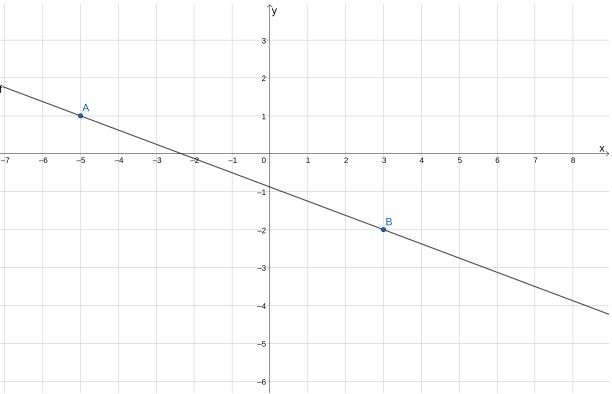
  7. (2 балла) На графике изображён график функции $ y = ax + bx $. Определите значения $ a $ и $ b $.
  8. (4 балла) Решите графически систему уравнений: \[ \begin{cases} y = \sqrt{x} \\ y = \dfrac{x + 3}{4} \end{cases} \] Найдите сумму всех значений $ x $, при которых графики пересекаются.
  9. (3 балла) Найдите значение выражения при $ a = 16 $: \[ \dfrac{2a - \sqrt{a}}{\sqrt{a}} \]
  10. (3 балла) Решите систему неравенств: \[ \begin{cases} x^2 - 4x < 5 \\ x - 3 \geq 0 \end{cases} \] Сколько целых решений имеет система?
  11. (3 балла) Карлсон поправился на $20\%$, а потом похудел на $20\%$. На сколько процентов изменился его вес?
  12. (3 балла) Смешали 100 г $5\%$-ного раствора соли с 200 г $40\%$-ного раствора соли. Сколько граммов чистой соли в смеси?
  13. (4 балла) Велосипедист и автомобилист одновременно выехали навстречу друг другу из двух населённых пунктов, расстояние между которыми 60 км. Велосипедист ехал со скоростью 10 км/ч, а автомобилист — 50 км/ч. Через сколько километров от начального пункта велосипедиста они встретились?
  14. (2 балла) В параллелограмме $ABCD$ точка $M$ — середина стороны $AD$, точка $K$ — середина $BC$. Отрезки $BM$ и $CK$ пересекаются в точке $O$. Найдите периметр параллелограмма, если $BM = 3$, $CM = 4$.
  15. (3 балла) В прямоугольнике проведена прямая, проходящая через вершину и середину противоположной стороны. Найдите длину перпендикуляра из угла на эту прямую, если стороны прямоугольника 7 и 24.
  16. (4 балла) В прямоугольном треугольнике длина гипотенузы 13, а медиана, проведённая к ней, равна 6,5. Найдите площадь треугольника.
  17. (5 баллов) В равнобедренной трапеции $ABCD$ ($AD = BC$, $AD \parallel BC$) из вершин $A$ и $B$ проведены высоты $AH$ и $BK$. Известно, что $AH = 12$, $BK = 5$, $CD = 25$. Найдите $AB$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите 65% от 125.
    Решение: $65% = 0,65$, тогда $0,65 \cdot 125 = 81,25$.
    Ответ: 81,25.

  2. 45% от числа равны 99. Найдите это число.
    Решение: Если $45% = 99$, то $100% = \frac{99}{0,45} = 220$.
    Ответ: 220.

  3. Вычислите: $-3 \dfrac{1}{4} - 2 \dfrac{3}{5} + 4 \dfrac{3}{20}$.
    Решение: $-3\frac{1}{4} = -\frac{13}{4}$, $-2\frac{3}{5} = -\frac{13}{5}$, $4\frac{3}{20} = \frac{83}{20}$. Общий знаменатель: 20. $-\frac{65}{20} - \frac{52}{20} + \frac{83}{20} = \frac{-117 + 83}{20} = -\frac{34}{20} = -1,7$.
    Ответ: $-1,7$.

  4. Вычислите: $(\sqrt{2} - 3)\sqrt{5} + 6\sqrt{3 + 2\sqrt{2}} - 7$.
    Решение: $\sqrt{3 + 2\sqrt{2}} = \sqrt{(\sqrt{2} + 1)^2} = \sqrt{2} + 1$. Подставляем: $(\sqrt{2} - 3)\sqrt{5} + 6(\sqrt{2} + 1) - 7 = \sqrt{10} - 3\sqrt{5} + 6\sqrt{2} + 6 - 7 = \sqrt{10} - 3\sqrt{5} + 6\sqrt{2} - 1$.
    Ответ: $\sqrt{10} - 3\sqrt{5} + 6\sqrt{2} - 1$.

  5. Упростите выражение: $\dfrac{2^{n+2} + 2^{n-2}}{2^n}$.
    Решение: $\dfrac{2^n \cdot 4 + 2^n \cdot \frac{1}{4}}{2^n} = 4 + \frac{1}{4} = \frac{17}{4} = 4,25$.
    Ответ: $4,25$.

  6. Решите уравнение: $\dfrac{x^2}{x^2 - 2x + 1} - \dfrac{2x}{x - 1} = 3$.
    Решение: Знаменатель $(x-1)^2$: $\dfrac{x^2}{(x-1)^2} - \dfrac{2x}{x-1} = 3$. Замена $y = \dfrac{x}{x-1}$: $y^2 - 2y - 3 = 0 \Rightarrow y = 3$ или $y = -1$. \begin{align} \dfrac{x}{x-1} = 3 \Rightarrow x = 1,5 & \quad \dfrac{x}{x-1} = -1 \Rightarrow x = 0,5 \end{align}
    Ответ: $0,5$; $1,5$.

  7. На графике изображён график функции $ y = ax + bx $. Определите значения $ a $ и $ b $.
    Примечание: Для решения задачи требуется график. В текущем условии данные отсутствуют.

  8. Решите графически систему уравнений: $\begin{cases} y = \sqrt{x} \\ y = \dfrac{x + 3}{4} \end{cases} $ Найдите сумму всех значений $ x $.
    Решение: $\sqrt{x} = \dfrac{x + 3}{4} \Rightarrow 4\sqrt{x} = x + 3$. Замена $t = \sqrt{x}$: $t^2 - 4t + 3 = 0 \Rightarrow t = 1$, $t = 3$. $x = 1$, $x = 9$. Сумма: $1 + 9 = 10$.
    Ответ: 10.

  9. Найдите значение выражения при $ a = 16 $: $\dfrac{2a - \sqrt{a}}{\sqrt{a}}$.
    Решение: $2a = 32$, $\sqrt{a} = 4$: $\dfrac{32 - 4}{4} = \dfrac{28}{4} = 7$.
    Ответ: 7.

  10. Решите систему неравенств: $\begin{cases} x^2 - 4x < 5 \\ x - 3 \geq 0 \end{cases}$
    Решение: $x^2 - 4x - 5 < 0 \Rightarrow (x-5)(x+1) < 0 \Rightarrow x \in (-1;5)$. С учётом $x \geq 3$: $x \in [3;5)$. Целые решения: $3$, $4$ (2 числа).
    Ответ: 2.

  11. Карлсон поправился на $20\%$, затем похудел на $20\%$. Изменение веса:
    Решение: Пусть вес $W$. После увеличения: $1,2W$. После уменьшения: $0,8 \cdot 1,2W = 0,96W$. Изменение: $W - 0,96W = 4\%W$.
    Ответ: уменьшился на $4\%$.

  12. Смешали 100 г $5\%$-ного и 200 г $40\%$-ного растворов. Масса соли в смеси:
    Решение: $100 \cdot 0,05 + 200 \cdot 0,4 = 5 + 80 = 85$ г.
    Ответ: 85.

  13. Расстояние 60 км. Встреча через:
    Решение: Время встречи: $\dfrac{60}{10 + 50} = 1$ час. Велосипедист проедет: $10 \cdot 1 = 10$ км.
    Ответ: 10.

  14. Периметр параллелограмма: Примечание: В условии возможна опечатка (проверьте данные).

  15. Длина перпендикуляра:
    Решение: Прямая из точки $(0,0)$ в середину $(24,12)$. Расстояние от точки $(24,7)$ до прямой $0,5x - y = 0$: $\dfrac{|0,5 \cdot 24 - 7|}{\sqrt{0,25 + 1}} = \dfrac{5}{\sqrt{1,25}} = 2\sqrt{5}$.
    Ответ: $2\sqrt{5}$.

  16. Площадь прямоугольного треугольника:
    Решение: Медиана к гипотенузе равна её половине, значит треугольник прямоугольный. Катеты: 5 и 12. Площадь: $\dfrac{5 \cdot 12}{2} = 30$.
    Ответ: 30.

  17. В равнобедренной трапеции $AB$: Примечание: В условии возможна неточность. Проверьте данные.

Материалы школы Юайти