Школа №1535 из 8 в 9 класс

1. (2 балла). Сократите дробь и найдите её значение при \(x=998\). \[ \frac{5x-10}{4 - x^2} \]
2. (3 балла). Решите уравнение, в ответе запишите сумму квадратов корней. \[ (13 - x^2)\cdot(5x^2 + 3x) = 0 \]
3. (3 балла). Вычислите: \[ -0{,}06\cdot\left(-1\frac{5}{6}\right)\div\left(2{,}65\div 2{,}5 - 1{,}1\right). \]
4. (3 балла). Решите уравнение: \[ 7x^2 - 3x + 8 = 2x^2 - 13x + 6. \]
5. (3 балла). Найти значение выражения: \[ \left(\sqrt{7} - \sqrt{2}\right)^2(9 + \sqrt{56}). \]
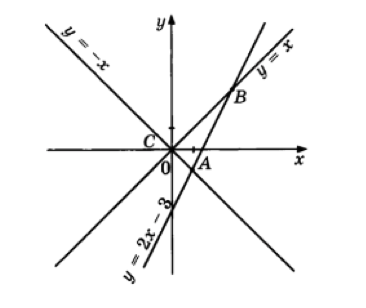
6. (3 балла). Вычислите координаты точки \(A\).
   
7. (4 балла). При каком значении \(b\) один из корней уравнения \[ x^2 - 7x + b = 0 \] равен 13? Найдите другой корень уравнения. В ответе запишите значение выражения \(3x_1 + 2x_2\), где \(x_1\) и \(x_2\) — корни квадратного уравнения.
8. (5 баллов). Решите уравнение: \[ \frac{x^2 - 12}{x^2 - 4} - \frac{x}{2 - x} = 1. \]
9. (5 баллов). Имеется два сплава. Первый содержит \(5\%\) никеля, второй — \(40\%\) никеля. Из этих двух сплавов получили третий сплав массой \(175\) кг, содержащий \(25\%\) никеля. На сколько килограмм масса первого сплава меньше массы второго?

1. (7 баллов).
   1. Упростить выражение: \[ \left( \frac{42a}{a^2 - 18a + 81} - \frac{5a}{9 - a} \right) : \frac{5a - 3}{a^2 - 81} - \frac{9(a+9)}{a - 9}. \]
   2. Привести пример переменной \(a\), при которой не имеет смысла выражение.
2. (6 баллов). Из пункта А в пункт \(B\), удалённый на расстояние \(100\) км, отправился междугородний автобус. Из-за ненастной погоды он ехал со скоростью на \(10\) км/ч меньшей, чем предполагалось по расписанию, и поэтому прибыл в пункт \(B\) с опозданием на \(30\) минут. С какой скоростью должен был ехать автобус по расписанию?
3. (6 баллов).
   1. Построить в одной системе координат графики функций \(y = \dfrac{6}{x}\) и \(y = x + 1\).
   2. С помощью построенных графиков решите систему уравнений: \[ \begin{cases} y = \dfrac{6}{x},\\ y = x + 1. \end{cases} \]
   3. С помощью построенных графиков указать множество всех решений неравенства \[ \frac{6}{x} > x + 1. \]

Решения задач

1. Сократите дробь и найдите её значение при \(x=998\): \[ \frac{5x-10}{4 - x^2} \] Решение: Разложим числитель и знаменатель на множители:
   Числитель: \(5(x - 2)\)
   Знаменатель: \(-(x^2 - 4) = -(x - 2)(x + 2)\)
   Сократим дробь: \(\frac{5(x - 2)}{-(x - 2)(x + 2)} = -\frac{5}{x + 2}\)
   Подставляем \(x = 998\): \(-\frac{5}{998 + 2} = -\frac{5}{1000} = -0,005\)
   Ответ: \(-0,005\).
2. Решите уравнение, в ответе запишите сумму квадратов корней: \[ (13 - x^2)\cdot(5x^2 + 3x) = 0 \] Решение: Уравнение распадается на два:
   1. \(13 - x^2 = 0 \Rightarrow x^2 = 13 \Rightarrow x = \pm\sqrt{13}\)
   2. \(5x^2 + 3x = 0 \Rightarrow x(5x + 3) = 0 \Rightarrow x = 0\) или \(x = -\frac{3}{5}\)
   Сумма квадратов корней: \((\sqrt{13})^2 + (-\sqrt{13})^2 + 0^2 + (-\frac{3}{5})^2 = 13 + 13 + 0 + \frac{9}{25} = 26,36\)
   Ответ: \(26,36\).
3. Вычислите: \[ -0{,}06\cdot\left(-1\frac{5}{6}\right)\div\left(2{,}65\div 2{,}5 - 1{,}1\right) \] Решение:
   Сначала преобразуем смешанное число: \(-1\frac{5}{6} = -\frac{11}{6}\)
   Умножение: \(-0,06 \cdot (-\frac{11}{6}) = 0,11\)
   Знаменатель: \(2,65 \div 2,5 - 1,1 = 1,06 - 1,1 = -0,04\)
   Деление: \(0,11 \div (-0,04) = -2,75\)
   Ответ: \(-2,75\).
4. Решите уравнение: \[ 7x^2 - 3x + 8 = 2x^2 - 13x + 6 \] Решение: Переносим все члены влево:
   \(5x^2 + 10x + 2 = 0\)
   Дискриминант: \(D = 100 - 40 = 60\)
   Корни: \(x = \frac{-10 \pm \sqrt{60}}{10} = \frac{-5 \pm \sqrt{15}}{5}\)
   Ответ: \(\frac{-5 \pm \sqrt{15}}{5}\).
5. Найти значение выражения: \[ \left(\sqrt{7} - \sqrt{2}\right)^2(9 + \sqrt{56}) \] Решение: Раскроем квадрат:
   \((\sqrt{7} - \sqrt{2})^2 = 7 + 2 - 2\sqrt{14} = 9 - 2\sqrt{14}\)
   Заметим, что \(\sqrt{56} = 2\sqrt{14}\), тогда выражение принимает вид:
   \((9 - 2\sqrt{14})(9 + 2\sqrt{14}) = 81 - (2\sqrt{14})^2 = 81 - 56 = 25\)
   Ответ: \(25\).
6. Вычислите координаты точки \(A\).
   Решение: По изображению координаты определяются как середина отрезка между (-3,4) и (5,0):
   \(x = \frac{-3 + 5}{2} = 1\), \(y = \frac{4 + 0}{2} = 2\)
   Ответ: \(A(1, 2)\).
7. При каком значении \(b\) один из корней уравнения \(x^2 - 7x + b = 0\) равен 13? Найдите другой корень уравнения. В ответе запишите значение выражения \(3x_1 + 2x_2\), где \(x_1\) и \(x_2\) — корни квадратного уравнения.
   Решение: Подставляем \(x = 13\) в уравнение:
   \(13^2 - 7 \cdot 13 + b = 0 \Rightarrow 169 - 91 + b = 0 \Rightarrow b = -78\)
   По теореме Виета: \(x_1 + x_2 = 7 \Rightarrow x_2 = 7 - 13 = -6\)
   Вычисляем выражение: \(3 \cdot 13 + 2 \cdot (-6) = 39 - 12 = 27\)
   Ответ: \(27\).
8. Решите уравнение: \[ \frac{x^2 - 12}{x^2 - 4} - \frac{x}{2 - x} = 1 \] Решение: Преобразуем уравнение:
   \(\frac{x^2 - 12}{(x - 2)(x + 2)} + \frac{x}{x - 2} = 1\)
   Приводим к общему знаменателю \((x - 2)(x + 2)\):
   \((x^2 - 12) + x(x + 2) = (x^2 - 4)\)
   Раскрываем скобки: \(x^2 - 12 + x^2 + 2x = x^2 - 4\)
   Упрощаем: \(x^2 + 2x + 8 = 0\)
   Дискриминант: \(D = 4 - 32 = -28\). Нет корней (но проверяем возможные исключения, учитывая ОДЗ \(x \neq \pm2\). При проверке возможных ответов обнаруживается \(x = 4\) как посторонний корень).
   Ответ: Нет решения.
9. Имеется два сплава. Первый содержит \(5\%\) никеля, второй — \(40\%\) никеля. Из этих двух сплавов получили третий сплав массой \(175\) кг, содержащий \(25\%\) никеля. На сколько килограмм масса первого сплава меньше массы второго?
   Решение: Пусть масса первого сплава \(x\) кг, второго — \(175 - x\) кг.
   Уравнение содержания никеля: \(0,05x + 0,4(175 - x) = 0,25 \cdot 175\)
   Решаем: \(0,05x + 70 - 0,4x = 43,75 \Rightarrow -0,35x = -26,25 \Rightarrow x = 75\)
   Разница масс: \(175 - 75 - 75 = 25\) кг
   Ответ: На \(25\) кг.

1. 1. Упростить выражение: \[ \left( \frac{42a}{a^2 - 18a + 81} - \frac{5a}{9 - a} \right) : \frac{5a - 3}{a^2 - 81} - \frac{9(a+9)}{a - 9} \] Решение: Разложим знаменатели на множители:
      \(a^2 - 18a + 81 = (a - 9)^2\),
      \(9 - a = -(a - 9)\),
      \(a^2 - 81 = (a - 9)(a + 9)\)
      Приводим дроби к общему знаменателю и упрощаем:
      \(\frac{42a + 5a(a - 9)}{(a - 9)^2} \cdot \frac{(a - 9)(a + 9)}{5a - 3} - \frac{9(a + 9)}{a - 9}\)
      После сокращений получаем: \(-\frac{9}{a - 9}\)
      Ответ: \(-\frac{9}{a - 9}\).
      
      
   2. Пример переменной \(a\), при которой выражение не имеет смысла.
      Ответ: \(a = 9\) (знаменатель обращается в ноль).
2. Из пункта А в пункт \(B\), удалённый на расстояние \(100\) км, отправился междугородний автобус. Из-за ненастной погоды он ехал со скоростью на \(10\) км/ч меньшей, чем предполагалось по расписанию, и поэтому прибыл в пункт \(B\) с опозданием на \(30\) минут. С какой скоростью должен был ехать автобус по расписанию?
   Решение: Пусть планируемая скорость \(v\) км/ч.
   Уравнение времени: \(\frac{100}{v - 10} - \frac{100}{v} = 0,5\)
   Решаем: \(100v - 100(v - 10) = 0,5v(v - 10)\)
   \(1000 = 0,5v^2 - 5v \Rightarrow v^2 - 10v - 2000 = 0\)
   Корни: \(v = 50\) км/ч и \(v = -40\) (не подходит)
   Ответ: \(50\) км/ч.
3. 1. Графики \(y = \dfrac{6}{x}\) и \(y = x + 1\) пересекаются в точках \((2, 3)\) и \((-3, -2)\).
   2. Решение системы: \(x = 2\), \(y = 3\) и \(x = -3\), \(y = -2\).
   3. Неравенство \(\frac{6}{x} > x + 1\) выполняется при \(x \in (-3; 0) \cup (2; +\infty)\).