8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 7 в 8 класс 2025 год демоверсия

Сложность:
Дата экзамена: 2025
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©


Демовариант вступительного испытания по математике в 8 ГУМ и 8 ЕН классы ГБОУ Школы № 1535



Инструкция

Вступительное испытание проводится с применением компьютеров. На выполнение всей работы отводится 60 минут. Задания работы – это задания с кратким ответом. Ответом к каждому заданию может быть целое число или конечная десятичная дробь (разделитель между целой и дробной частью – запятая). При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Оценивание правильности выполнения заданий осуществляется с использованием программных средств. Баллы, полученные за задания, суммируются. Максимальное количество баллов за работу – 50. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Желаем успеха!



  1. (3 балла) Найдите значение выражения \[ 2\frac{1}{4}\,\cdot\!\bigl(-11\frac{2}{9} \;-\;(-5,4)\!:\!\tfrac{9}{35}\bigr). \]

  2. (3 балла) Чему равно число \[ \frac{3^{10}\cdot2^{73}}{98}\,? \]

  3. (3 балла) Чему равен корень уравнения \[ 0,4\,(6-4x) \;=\; 1,9 \;-\; 0,5\,(3x-7)\,? \]

  4. (3 балла) Параллельные прямые \(AB\) и \(CD\) пересекают прямую \(EF\) в точках \(K\) и \(M\) соответственно. Угол \(\angle FMD\) равен \(37^\circ\). Найдите угол \(\angle AKM\).

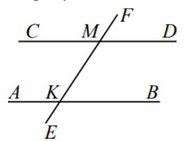
  5. (4 балла) Упростите выражение \[ \bigl(-0,3\,a^4 b\,c^3\bigr)^2 \;\cdot\; 5\,a^2\,c^6, \] приведя его к виду \(A\,a^k b^n c^m\), где \(A\) – числовой коэффициент, \(k,n,m\) – натуральные числа. В ответе запишите значение выражения \(A\cdot k\cdot n\cdot m\).

  6. (5 баллов) Чему равен коэффициент \(a\), при котором коэффициент при \(x^2\) в стандартном виде многочлена \((x^2+2x)(x^2 - a x + 6)\) равен нулю?

  7. (4 балла) В треугольнике \(ABC\) известно, что \(\angle BAC = 56^\circ\). Биссектриса угла \(BAC\) пересекает сторону \(BC\) в точке \(K\). \(\angle AKC = 104^\circ\). Чему равен угол \(ABC\)?

  8. (4 балла) Чему равно значение \(a\), если выполнено тождество \[ \bigl(0,2\,n - \tfrac{5}{2}m^2\bigr)^2 \;=\; \tfrac{n^2}{25} \;+\; a\,n\,m^2 \;+\; 6,25\,m^4\;? \]

  9. Разложите многочлен на множители (выберите верный ответ из предложенных, в ответе укажите его номер)
    1. (а) (2 балла) \(5m^2 - 10mn + 5n^2\).
      Варианты ответов:
      1) \((5m+1)^2\)
      2) \(5(m-n)^2\)
      3) \(5(m^2-n^2)\)
      4) \((5m+n)^2\)
      5) разложить нельзя.

    2. (б) (2 балла) \(2 - cx - x + 2c\).
      Варианты ответов:
      1) \((1+c)(2+x)\)
      2) \((1-c)(2-x)\)
      3) \(2(c - x + 1)\)
      4) \((1+c)(2-x)\)
      5) разложить нельзя.

    3. (в) (3 балла) \(9x^2 + 6x + 1 - 4y^2\).
      Варианты ответов:
      1) \((9x - y)(x + 4y)\)
      2) \((3x - 2y)(3x + 2y + 1)\)
      3) \((3x + 2y + 1)(3x - 2y \mp 1)\)
      4) \((3x - 1 + 2y)(3x + 1 + 2y)\)
      5) разложить нельзя.


  10. (4 балла) Смешали 4 л воды 20-% раствора вещества с 6 л 40-% раствора того же вещества. Сколько процентов составляет концентрация получившегося раствора?

  11. (5 баллов) Упростите выражение \[ (a+1)(a-1)(a^2+1) \;-\; (9 + a^2)^2 \] и найдите его значение при \(a = \tfrac{1}{3}\). Ответ: \(-84\)

  12. (5 баллов) Длина прямоугольника на 3 дм больше его ширины. Если длину уменьшить на 2 дм, а ширину увеличить на 5 дм, то площадь прямоугольника увеличится на 14 кв. дм. Чему равна площадь увеличенного прямоугольника в кв. дм? Ответ: \(32\)


Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значение выражения \[ 2\frac{1}{4} \cdot \left(-11\frac{2}{9} - (-5,4) : \frac{9}{35}\right). \] Решение: \[ -5,4 : \frac{9}{35} = -\frac{54}{10} \cdot \frac{35}{9} = -21; \quad -11\frac{2}{9} + 21 = -11\frac{2}{9} + \frac{189}{9} = \frac{88}{9}; \quad 2\frac{1}{4} \cdot \frac{88}{9} = \frac{9}{4} \cdot \frac{88}{9} = 22. \] Ответ: 22.

  2. Чему равно число \[ \frac{3^{10} \cdot 2^{73}}{98}? \] Решение: \[ 98 = 2 \cdot 7^2 \quad \Rightarrow \quad \frac{3^{10} \cdot 2^{73}}{2 \cdot 7^2} = 3^{10} \cdot 2^{72} \cdot \frac{1}{7^2}. \] Ответ: \( \frac{3^{10} \cdot 2^{72}}{49} \).

  3. Чему равен корень уравнения \[ 0,4\,(6 - 4x) = 1,9 - 0,5\,(3x - 7)? \] Решение: \[ 2,4 - 1,6x = 1,9 - 1,5x + 3,5; \quad 2,4 - 5,4 = -1,5x + 1,6x; \quad -3 = 0,1x; \quad x = -30. \] Ответ: \(-30\).

  4. Параллельные прямые \(AB\) и \(CD\) пересекают \(EF\) в точках \(K\) и \(M\). \(\angle FMD = 37^\circ\). Найдите \(\angle AKM\). Решение: \(\angle FMD = \angle AKM = 37^\circ\) (соответственные углы). Ответ: \(37^\circ\).

  5. Упростить выражение \[ \left(-0,3a^4bc^3\right)^2 \cdot 5a^2c^6. \] Решение: \[ (0,09a^8b^2c^6) \cdot 5a^2c^6 = 0,45a^{10}b^2c^{12}; \quad A \cdot k \cdot n \cdot m = 0,45 \cdot 10 \cdot 2 \cdot 12 = 108. \] Ответ: 108.

  6. Найти коэффициент \(a\), при котором коэффициент при \(x^2\) в \((x^2 + 2x)(x^2 - ax + 6)\) равен нулю. Решение: \[ x^4 + (-a + 2)x^3 + (6 - 2a)x^2 + \ldots; \quad 6 - 2a = 0 \quad \Rightarrow \quad a = 3. \] Ответ: 3.

  7. В \(\triangle ABC\): \(\angle BAC = 56^\circ\), биссектриса \(AK\), \(\angle AKC = 104^\circ\). Найдите \(\angle ABC\): Решение: \[ \angle KAC = 28^\circ; \quad \angle ACB = 180^\circ - 28^\circ - 104^\circ = 48^\circ; \quad \angle ABC = 180^\circ - 56^\circ - 48^\circ = 76^\circ. \] Ответ: \(76^\circ\).

  8. Найти \(a\) в тождестве \[ (0,2n - 2,5m^2)^2 = \frac{n^2}{25} + anm^2 + 6,25m^4. \] Решение: \[ 0,04n^2 - nm^2 + 6,25m^4 \Rightarrow a = -1. \] Ответ: \(-1\).

  9. Разложить на множители:
    1. (a) \(5m^2 - 10mn + 5n^2 = 5(m - n)^2\) — 2.
    2. (б) \(2 - cx - x + 2c = (1 + c)(2 - x)\) — 4.
    3. (в) \(9x^2 + 6x + 1 - 4y^2 = (3x + 1 - 2y)(3x + 1 + 2y)\) — 3.


  10. Концентрация раствора после смешивания: Решение: \[ \text{Вещество: } 0,2 \cdot 4 + 0,4 \cdot 6 = 3,2 \text{ л;} \quad \text{Объем: } 10 \text{ л;} \quad \frac{3,2}{10} = 32\%. \] Ответ: 32.

  11. Упростить выражение \[ (a + 1)(a - 1)(a^2 + 1) - (9 + a^2)^2. \] Решение: \[ a^4 - 1 - (a^4 + 18a^2 + 81) = -18a^2 - 82; \quad \text{При } a = \frac{1}{3}: -18 \cdot \frac{1}{9} - 82 = -84. \] Ответ: \(-84\).

  12. Площадь увеличенного прямоугольника: Решение: \[ \begin{cases} l = w + 3, \\ (l - 2)(w + 5) = lw + 14. \end{cases} \quad \Rightarrow w = 3, \quad l = 6; \quad \text{Новая площадь: } 4 \cdot 8 = 32. \] Ответ: 32.
Материалы школы Юайти