8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 6 в 7 класс 2022 год вариант 1

Сложность:
Дата экзамена: 2022
Сложность:
Дата экзамена: 2022
youit.school ©

ЛИЦЕЙ №1535


2022 год




  1. Дан квадрат $15 \times 15$. По сторонам квадрата вырезали прямоугольник площадью 70 клеток. Найдите периметр этого прямоугольника, если сторона клеточки равна 4.
  2. Человек продал акции за 1400 рублей, и это составило ему ущерб, равный $6 \dfrac{2}{3}\%$. За сколько ему нужно было бы продать акции, чтобы выйти в плюс на $33 \dfrac{1}{3}\%$?
  3. В деревне жители любят кошек и собак. В 20% домов, где живут собаки, живут и кошки. А в 25% домов, где живут кошки, там живут и собаки. В 20% домов вообще нет животных. Сколько процентов домов составляют дома, где живут и кошки, и собаки?
  4. На 4-х заводах работают 590 человек. На третьем заводе работают 13% от количества второго завода, количество рабочих на третьем относится к количеству на первом как 3:4, и т.д. Составьте уравнение и найдите количество рабочих на каждом заводе.
  5. Задача на разрезание: была дана достаточно необычная фигура. Нужно было получить квадраты.
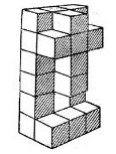
  6. Саша тратит 2 г краски. Сколько краски понадобится на покраску поверхности фигуры из 27 кубиков, показанной на рисунке?
  7. Задача на биссектрисы углов.
  8. Часы показывают 20:22. Сколько градусов между стрелками?
  9. В ряд записаны числа от 1 до 9. Какое число нужно убрать, чтобы получился наименьший возможный НОД?



Второй поток



  1. Поезд равномерно едет со скоростью 72 км/ч. Он прошёл лесополосу за 1 минуту. Какова длина поезда?
  2. Сейчас 14:00. Через какое время минутная и часовая стрелка встретятся снова?
  3. Маша решала задачи четыре дня: в первый день она решила в полтора раза больше задач, чем во второй, в третий — 75% от второго, в четвёртый — 9 задач. Всего — 256. Сколько задач решила Маша в каждый из дней?
  4. Вода составляет 84% массы обезвоженного верблюда. Когда верблюд напился, вода стала составлять 85% массы, и он стал весить 800 кг. Сколько весит обезвоженный верблюд?
    1. Было 1535 полосок. Некоторые из них разрезали на 4 части, и стало 1595 полосок. Сколько полосок разрезали?
    2. Было 1535 полосок. Некоторые из них разрезали на 4 части, и получилось 2021 полоска. Могло ли такое быть?
  6. Задача на кубики.
  7. Задача на разрезание.
  8. Уравнение.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Дан квадрат $15 \times 15$. По сторонам квадрата вырезали прямоугольник площадью 70 клеток. Найдите периметр этого прямоугольника, если сторона клеточки равна 4.
    Решение: Площадь прямоугольника — 70 клеток. Возможные размеры: $7 \times 10$ или $10 \times 7$. Периметр: $2 \cdot (7 + 10) = 34$ клетки. С учётом размера клетки: $34 \cdot 4 = 136$ см.
    Ответ: 136 см.
  2. Человек продал акции за 1400 рублей, и это составило ему ущерб, равный $6 \dfrac{2}{3}\%$. За сколько нужно продать акции для прибыли $33 \dfrac{1}{3}\%$?
    Решение: Первоначальная стоимость: $1400 : \left(1 - \dfrac{20}{3}\%\right) = 1400 \cdot \dfrac{3}{2.8} = 1500$ руб. Цена с прибылью: $1500 \cdot \left(1 + \dfrac{1}{3}\right) = 2000$ руб.
    Ответ: 2000 руб.
  3. В деревне 20% домов с собаками содержат кошек, 25% домов с кошками содержат собак, 20% домов без животных. Сколько % домов с обоими животными?
    Решение: Пусть $x$% — дома с обоими животными. Тогда:
    $x = 20% \cdot S \Rightarrow S = 5x$,
    $x = 25% \cdot C \Rightarrow C = 4x$.
    Общее количество: $5x + 4x - x + 20 = 100 \Rightarrow 8x = 80 \Rightarrow x = 10\%$.
    Ответ: 10\%.
  4. На 4 заводах 590 человек. На третьем — 13% от второго. Отношение третьего к первому 3:4. Составьте уравнение и найдите количество рабочих.
    Решение:
    Пусть $S_2$ — рабочие второго завода. Тогда:
    $S_3 = 0.13S_2$,
    $S_1 = \dfrac{4}{3}S_3 = \dfrac{4}{3} \cdot 0.13S_2 = \dfrac{0.52}{3}S_2$.
    Если $S_4$ — рабочие четвертого завода:
    $\dfrac{0.52}{3}S_2 + S_2 + 0.13S_2 + S_4 = 590$.
    Для полного решения требуется дополнительная информация о $S_4$.
  5. Задача на разрезание. Решение зависит от конкретной фигуры.
  6. Саша тратит 2 г краски на кубик. Поверхность фигуры из 27 кубиков. Ответ зависит от количества окрашенных граней.
    Решение: Куб 3x3x3 имеет 54 внешних грани. Каждая грань кубика — одна грань фигуры. Краска: $54 \cdot 2 = 108$ г.
    Ответ: 108 г.
  7. Задача на биссектрисы. Требуется конкретное условие.
  8. Часы показывают 20:22. Угол между стрелками:
    Решение: Формула угла: $|\dfrac{720}{11} - (20 \cdot 30 + 22 \cdot 0.5)| = |479 - 600| = 119^\circ$.
    Ответ: $119^\circ$.
  9. Убрать число из ряда 1-9 для минимального НОД.
    Решение: НОД чисел 1-9 без одного равен 1 (например, убрав 5).
    Ответ: Любое число. Второй поток:
  10. Поезд длиной $L$ прошёл лесополосу за 1 минуту при скорости 72 км/ч.
    Решение: $L = 72 \cdot \dfrac{1}{60} = 1.2$ км = 1200 м.
    Ответ: 1200 м.
  11. Встреча стрелок после 14:00:
    Решение: Через $\dfrac{60}{5.5} = 10 \dfrac{10}{11}$ мин.
    Ответ: 10 $\dfrac{10}{11}$ мин.
  12. Маша решила задачи:
    Решение: Пусть во второй день $x$ задач. Тогда: $1.5x + x + 0.75x + 9 = 256 \Rightarrow x = 76$.
    Ответ: 114, 76, 57, 9.
  13. Вес верблюда:
    Решение: Сухая масса — $15\%$ от 800 кг = 120 кг = $16\%$ исходной. Исходный вес: $120 : 0.16 = 750$ кг.
    Ответ: 750 кг.
    1. Разрезали $k$ полосок: $1535 + 3k = 1595 \Rightarrow k = 20$.
      Ответ: 20.
    2. $1535 + 3k = 2021 \Rightarrow k = 162$ (возможно).
      Ответ: Да.
  15. Задачи на кубики и разрезание требуют изображения.
Материалы школы Юайти