8 800 707 6729
8 800 707 6729Telegram канал

Школа №1535 из 6 в 7 класс 2020 год вариант 1-2

Сложность:
Дата экзамена: 2020
Сложность:
Дата экзамена: 2020
youit.school ©

ЛИЦЕЙ №1535


2020 год



Инструкция: 1. Вступительное испытание проводится в письменной форме. Использование калькуляторов, компьютеров и любых видов справочных пособий запрещено. На время проведения вступительного испытания необходимо отключить мобильные телефоны и любые другие виды коммуникаторов, в том числе смарт-часы. Взаимные консультации учащихся запрещены. Работа выполняется и оформляется исключительно на листах, выданных Вам экзаменаторами. Нарушение любого пункта инструкции влечёт удаление учащегося из аудитории и выставление ему за вступительное испытание по математике отметки «0». Продолжительность экзамена 90 минут. 2. Ответом на задание этого экзамена может быть или целое число, или конечная десятичная дробь, или несократимая обыкновенная дробь (с выделенной целой частью). Полученный Вами ответ следует вписать в соответствующую строку бланка ответов справа от номера задачи. Цифры, знак "минус", дробные черты, десятичные запятые должны быть написаны чётко, разборчиво. Единицы измерения в бланк не вносятся. При проверке заданий этого этапа экзамена проверяется только бланк с Вашими ответами. Претензии, связанные с неразборчиво написанными цифрами, при показе работ не обсуждаются.


  1. (Каждый пример — 2 балла). Вычислите:
    1. \( \dfrac{4}{12} + \dfrac{6}{7} \cdot \dfrac{3}{5} \)
    2. \( \dfrac{18}{9} - \dfrac{11}{34} \cdot \dfrac{2}{11} \)
    3. \( \dfrac{1}{5} \cdot \dfrac{20}{27} \)
    4. \( \dfrac{3}{13} : \dfrac{2}{33} \)
    5. \( 1{,}6 \cdot 7{,}09 \)
    6. \( 13{,}68 : 4{,}5 \)
    7. \( 2 - 12{,}3 + 5{,}9 - 1{,}9 \)


  2. (3 балла) Гэндальф имел рост 1 м 85 см. Рост гнома Гимли составляет 40% от роста Гэндальфа. Найдите рост Гимли в сантиметрах.

  3. (3 балла) Найдите сумму: \( 0{,}3 + 0{,}8 + 0{,}4 + 1{,}6 \)

  4. (3 балла) Расстояние между городами A и B равно 105 км. Автомобиль проехал \( \dfrac{5}{7} \) этого расстояния за полтора часа. Найдите скорость автомобиля в км/ч.

  5. (3 балла) Масштаб карты: 1 см соответствует 900 м. Сколько сантиметров составляет расстояние между пунктами A и B на карте, если на местности оно равно 4{,}05 км?

  6. (3 балла) 6 одинаковых труб заполняют бассейн за 15 часов. На сколько часов быстрее заполнится бассейн, если труб станет на 3 больше?

  7. (3 балла) За день продали 750 кг картофеля, что составляет 15% от всего количества. Сколько тонн картофеля завезли в магазин?

  8. (3 балла) Длина прямоугольника — 56 см, ширина составляет \( \dfrac{4}{7} \) от длины. Чему равна площадь квадрата, имеющего такой же периметр, как этот прямоугольник?

  9. (3 балла) Найдите значение переменной \( y \), если: \[ \left( \dfrac{3}{7} : \dfrac{1}{14} \right) = 0{,}4 : (y - 4) \]

  10. (4 балла) Точки \( A \), \( B \), \( C \) лежат на координатной прямой. \( A = 7 \), \( B = -2 \), точка \( C \) имеет положительную координату, причём \( AB = \dfrac{1}{3} \cdot BC \). Найдите координату точки \( C \).

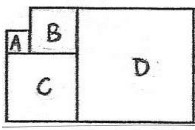
  11. (4 балла) Фигуры \( A \), \( B \), \( C \), \( D \) — квадраты. Периметр квадрата \( A \) равен 12 см и составляет \( \dfrac{3}{5} \) периметра квадрата \( B \). Чему равна площадь квадрата \( D \)?


  12. (4 балла) В магазине 1 кг гречки стоит 96 рублей. В другом — 90 рублей, но дорога туда-обратно стоит 50 рублей. Какое наименьшее количество килограммов гречки надо купить, чтобы поездка была выгодной?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите:
    1. \( \dfrac{4}{12} + \dfrac{6}{7} \cdot \dfrac{3}{5} = \dfrac{1}{3} + \dfrac{18}{35} = \dfrac{35}{105} + \dfrac{54}{105} = \dfrac{89}{105} \).
      Ответ: \( \dfrac{89}{105} \).

    2. \( \dfrac{18}{9} - \dfrac{11}{34} \cdot \dfrac{2}{11} = 2 - \dfrac{2}{34} = 2 - \dfrac{1}{17} = \dfrac{34}{17} - \dfrac{1}{17} = \dfrac{33}{17} = 1 \dfrac{16}{17} \).
      Ответ: \( 1 \dfrac{16}{17} \).

    3. \( \dfrac{1}{5} \cdot \dfrac{20}{27} = \dfrac{20}{135} = \dfrac{4}{27} \).
      Ответ: \( \dfrac{4}{27} \).

    4. \( \dfrac{3}{13} : \dfrac{2}{33} = \dfrac{3}{13} \cdot \dfrac{33}{2} = \dfrac{99}{26} = 3 \dfrac{21}{26} \).
      Ответ: \( 3 \dfrac{21}{26} \).

    5. \( 1{,}6 \cdot 7{,}09 = 11{,}344 \).
      Ответ: 11,344.

    6. \( 13{,}68 : 4{,}5 = 3{,}04 \).
      Ответ: 3,04.

    7. \( 2 - 12{,}3 + 5{,}9 - 1{,}9 = (2 - 12{,}3) + (5{,}9 - 1{,}9) = -10{,}3 + 4 = -6{,}3 \).
      Ответ: -6,3.


  2. Рост Гэндальфа — 185 см. Рост Гимли: \( 185 \cdot 0{,}4 = 74 \) см.
    Ответ: 74.

  3. Сумма: \( 0{,}3 + 0{,}8 + 0{,}4 + 1{,}6 = 3{,}1 \).
    Ответ: 3,1.

  4. Пройденное расстояние: \( \dfrac{5}{7} \cdot 105 = 75 \) км. Скорость: \( \dfrac{75}{1{,}5} = 50 \) км/ч.
    Ответ: 50.

  5. Расстояние на карте: \( \dfrac{4050}{900} = 4{,}5 \) см.
    Ответ: 4,5.

  6. Время с 9 трубами: \( \dfrac{1}{\dfrac{9}{6} \cdot \dfrac{1}{15}} = 10 \) часов. Экономия: \( 15 - 10 = 5 \) часов.
    Ответ: 5.

  7. Весь картофель: \( \dfrac{750}{0{,}15} = 5000 \) кг = 5 т.
    Ответ: 5.

  8. Ширина: \( 56 \cdot \dfrac{4}{7} = 32 \) см. Периметр: \( 2 \cdot (56 + 32) = 176 \) см. Сторона квадрата: \( 176 : 4 = 44 \) см. Площадь: \( 44^2 = 1936 \) см².
    Ответ: 1936.

  9. Решение уравнения: \[ \dfrac{3}{7} : \dfrac{1}{14} = 6 = 0{,}4 : (y - 4) \implies y - 4 = \dfrac{0{,}4}{6} \implies y = 4 + \dfrac{1}{15} = 4{,}066... \]
    Ответ: \( 4 \dfrac{1}{15} \).

  10. Длина \( AB \): \( 7 - (-2) = 9 \). \( BC = 9 \cdot 3 = 27 \). Координата \( C \): \( -2 + 27 = 25 \).
    Ответ: 25.

  11. Сторона квадрата \( A \): 3 см. Сторона квадрата \( B \): 5 см. Площадь квадрата \( D \): \( 13 \times 13 = 169 \) см².
    Ответ: 169.

  12. Минимальное количество: \( \dfrac{50}{96 - 90} = \dfrac{50}{6} \approx 8{,}33 \). Наибольшее целое: 9 кг.
    Ответ: 9.
Материалы школы Юайти