Московская школа на Юго-Западе № 1543 из 4 в 5 класс 2025 год вариант 2

ЛИЦЕЙ №1543

2025 год

15.05.2025

Вариант 2

1. Решите задачу с пояснениями: Прямоугольник разрезали на семь равных квадратов. Оказалось, что сумма периметров этих семи квадратов на $132$ см больше, чем периметр исходного прямоугольника. Найдите площадь исходного прямоугольника.
2. Решите задачу с пояснениями: В супермаркет привезли мороженое двух видов: рожки и эскимо, всего $420$ штук. Рожков было в $5$ раз меньше, чем эскимо. Общая масса рожков составляла седьмую часть массы всего мороженого. Что и на сколько граммов тяжелее: один рожок или одно эскимо, если все рожки вместе весили $5$ кг $250$ г?
3. Вычислите: $40105-(708\cdot 406-135):139$.
4. Решите задачу с пояснениями: Маша и Оля идут навстречу друг другу, каждая из своего дома. Если они выйдут одновременно, то от места встречи будет по $2$ км до дома каждой из девочек. Но Оля вышла на $10$ минут раньше Маши, поэтому они встретились они на расстоянии $1$ км $800$ м до Машиного дома. За сколько времени Оля может дойти от своего дома до Машиного?
5. Запишите наименьшее шестизначное число, в котором цифр, больших $6$, не меньше, чем цифр, меньших $6$.
6. В буфете лежал квадратный кусок пастилы массой $64$ грамма. Мышка забралась в буфет и съела часть пастилы так, что остались три одинаковых квадратных кусочка. Периметр каждого из них вчетверо меньше периметра исходного кусочка. Сколько граммов пастилы досталось мышке?
7. В очень длинном поезде $23$ вагона, в которых разместились $524$ пассажира. Оказалось, что в любых четырёх подряд идущих вагонах находится ровно $90$ пассажиров. Сколько пассажиров в $16$-м вагоне?
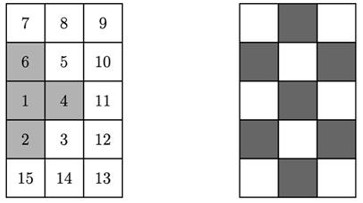
8. Миша пронумеровал все клетки таблицы, соблюдая правило: любая пара клеток с соседними номерами имеет общую сторону. Сумма номеров серых клеток у Миши равна $6+7+8+10=31$. Занумеруйте клетки пустой таблицы, соблюдая это же правило, но чтобы сумма чисел в четырёх серых клетках была как можно меньше.
   

Решения задач

1. Прямоугольник разрезали на семь равных квадратов. Сумма периметров квадратов на 132 см больше периметра прямоугольника. Найдите площадь прямоугольника.
   Решение: Пусть сторона квадрата равна \(a\). Тогда периметр одного квадрата \(4a\), сумма периметров семи квадратов: \(7 \cdot 4a = 28a\). Прямоугольник составлен из семи квадратов в ряд: его размеры \(7a \times a\). Периметр прямоугольника: \(2 \cdot (7a + a) = 16a\). Разность: \(28a - 16a = 12a = 132\). Отсюда \(a = 11\) см. Площадь прямоугольника: \(7a \cdot a = 7 \cdot 11 \cdot 11 = 847\) см\(^2\).
   Ответ: 847 см\(^2\).
2. В супермаркете рожков в 5 раз меньше, чем эскимо. Общая масса рожков — \(\frac{1}{7}\) всей массы мороженого. Определите, что тяжелее и на сколько.
   Решение: Всего мороженого 420 штук. Пусть рожков \(x\), тогда эскимо \(5x\): \(x + 5x = 420 \Rightarrow x = 70\), эскимо 350. Масса рожков 5,25 кг (\(\frac{1}{7}\) общей массы), значит общая масса \(5,25 \cdot 7 = 36,75\) кг. Масса эскимо: \(36,75 - 5,25 = 31,5\) кг. Масса одного рожка: \(\frac{5250 \text{ г}}{70} = 75 \text{ г}\). Масса эскимо: \(\frac{31500 \text{ г}}{350} = 90 \text{ г}\). Разница: \(90 - 75 = 15 \text{ г}\).
   Ответ: Эскимо тяжелее на 15 г.
3. Вычислите: \(40105 - (708 \cdot 406 - 135) : 139\).
   Решение: Выполним действия по порядку: \[ 708 \cdot 406 = 287\,448,\quad 287\,448 - 135 = 287\,313,\quad 287\,313 : 139 = 2\,067,\quad 40\,105 - 2\,067 = 38\,038. \] Ответ: $38\,038.$
4. Маша и Оля встретились на расстоянии $1\,800$ м от дома Маши. Определите время пути Оли.
   Решение: Расстояние между домами 4 км. При раннем выходе Оля прошла \(4 - 1,8 = 2,2\) км, Маша — 1,8 км. Пусть скорость девочек \(v\). Время Маши: \(\frac{1,8}{v}\) ч. Оля затратила на 10 минут (\( \frac{1}{6}\) ч) больше: \(\frac{2,2}{v} = \frac{1,8}{v} + \frac{1}{6}\). Отсюда \(v = 2,4\) км/ч. Время Оли: \(\frac{4}{2,4} = 1\,\text{ч}\,40\,\text{мин}\).
   Ответ: 100 минут.
5. Наименьшее шестизначное число с условием на цифры.
   Решение: Число содержит не менее трёх цифр \(\ge 7\). Минимальное число: $100\,777$ (цифры 1,0,0,7,7,7).
   Ответ:$ 100\,777.$
6. Мышка съела часть пастилы, остались три квадрата с периметром вчетверо меньше исходного. Найдите массу съеденной пастилы.
   Решение: Исходный квадрат со стороной 8 см (периметр 32 см). После остались три квадрата со стороной 2 см. Площадь исходной пастилы \(64 \text{ см}^2\), оставшейся — \(3 \cdot 4 = 12 \text{ см}^2\). Масса съеденной: \(64 - 12 = 52\) г.
   Ответ: 52 г.
7. В поезде $23$ вагона и всего $524$ пассажира. В любых $4$ соседних вагонах вместе ровно $90$ пассажиров. Сколько пассажиров в $16$-м вагоне?
   Решение:
   Посчитаем пассажиров в пяти подряд идущих ``четвёрках'': \[ (1\text{--}4),\ (5\text{--}8),\ (9\text{--}12),\ (13\text{--}16),\ (17\text{--}20). \] В каждой четвёрке по $90$, значит вместе:
   \[ 5 \times 90 = 450. \]
   Всего пассажиров $524$, значит в тех вагонах, которые мы ещё не посчитали (это $21$, $22$ и $23$), вместе:
   \[ 524 - 450 = 74. \]
   Сравним четвёрки $1\text{--}4$ и $2\text{--}5$: обе дают $90$.
   Тогда:
   \[ (2+3+4+5) - (1+2+3+4) = 0 \ \Rightarrow\ 5 = 1. \]
   Аналогично получаем, что числа в вагонах повторяются каждые $4$:
   \[ 6=2,\ 7=3,\ 8=4,\ \ldots \]
   Значит суммы в вагонах $21$–$23$ такие же, как в $1$–$3$:
   \[ 1 + 2 + 3 = 74. \]
   А в вагонах $1$–$4$ вместе $90$, значит в $4$-м:
   \[ 4 = 90 - (1+2+3) = 90 - 74 = 16. \]
   Поскольку всё повторяется через $4$ вагона, в $16$-м вагоне столько же, сколько в $4$-м:
   \[ a_{16} = a_4 = 16. \]
   Ответ:$ \boxed{16}.$
8. Раскрасим таблицу в «шахматные» цвета. Тогда всякий переход от номера $k$ к $k+1$ обязательно меняет цвет клетки (клетки имеют общую сторону $\Rightarrow$ разные цвета). Значит, все числа одного цвета образуют арифметическую прогрессию с шагом $2$: либо это нечётные $1,3,5,7,\dots$, либо чётные $2,4,6,8,\dots$.
   Заметим, что четыре выделенные (серые) клетки лежат на клетках одного цвета.
   Следовательно, числа на них неизбежно идут «через одно»:
   \[ \{1,3,5,7\}\quad\text{или}\quad\{2,4,6,8\}. \]
   Чтобы сумма была минимальной, нужно взять на серых клетках наименьшие возможные числа этого цвета, то есть $1,3,5,7$: \[ 1+3+5+7=16. \] Меньше получить невозможно, так как разместить одновременно $1,2,3,4$ на клетках одного цвета нельзя (соседние номера всегда разного цвета).
   Например, начнём нумерацию с серой клетки числом $1$ и пройдём все клетки «змейкой» (по строке слева направо, затем вниз и обратно, и т.\,д.). Тогда серые клетки действительно получат номера $1,3,5,7$.
   Ответ: минимальная сумма в четырёх серых клетках равна $16$.