Московская школа на Юго-Западе № 1543 из 4 в 5 класс 2025 год вариант 1

ЛИЦЕЙ №1543

2025 год

13.05.2025

Вариант 1

1. Решите задачу с пояснениями: Прямоугольник разрезали на пять равных квадратов. Оказалось, что сумма периметров этих пяти квадратов на $120$ см больше, чем периметр исходного прямоугольника. Найдите площадь исходного прямоугольника.
2. Решите задачу с пояснениями: В ларьке есть розы и гвоздики, всего $630$ цветов, причём роз в $6$ раз меньше, чем гвоздик. Общая стоимость всех роз составляет треть стоимости всех цветов. Что и на сколько рублей дороже, одна роза или одна гвоздика, если все розы, вместе взятые, стоят $24300$ рублей?
3. Вычислите: $50103-(405\cdot 709-381):138$.
4. Решите задачу с пояснениями: Петя и Вася идут друг другу навстречу, каждый из своего дома. Если они выйдут одновременно, то от места встречи будет по $1$ км до дома каждого из них. Но Петя вышел на $5$ минут раньше Васи, поэтому они встретились в $800$ метрах от Васиного дома. За сколько минут Петя может дойти от своего дома до Васиного?
5. Запишите наименьшее шестизначное число, в котором цифр, больших $6$, не меньше, чем цифр, меньших $6$.
6. Медвежата дали лисе квадратный ломтик сыра массой $72$ грамма. Лиса съела часть сыра так, что остались два одинаковых квадратных ломтика. Периметр каждого из них втрое меньше периметра исходного кусочка. Сколько граммов сыра съела лиса?
7. В библиотеке есть $20$ книжных полок, на которых расставлены $543$ книги. На любых трёх подряд идущих полках находится ровно $80$ книг. Сколько книг стоит на $12$-й полке?
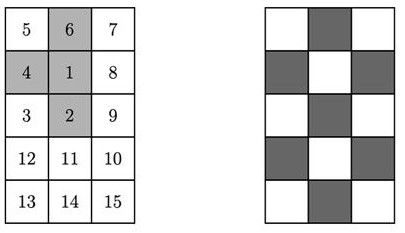
8. Галя пронумеровала все клетки таблицы, соблюдая правило: любая пара клеток с соседними номерами имеет общую сторону. Сумма номеров серых клеток у Гали равна $8+12+14+15=49$. Занумеруйте клетки пустой таблицы, соблюдая это же правило, но чтобы сумма чисел в четырёх серых клетках была как можно меньше.
   

Решения задач

1. Прямоугольник разрезали на пять равных квадратов. Сумма периметров пяти квадратов на 120 см больше периметра прямоугольника. Площадь исходного прямоугольника.
   Решение: Пусть сторона квадрата равна \( a \). Тогда прямоугольник состоит из пяти квадратов, его размеры \( 5a \times a \). Сумма периметров пяти квадратов:
   \( 5 \cdot 4a = 20a \). Периметр прямоугольника:
   \( 2(5a + a) = 12a \). Разность периметров:
   \( 20a - 12a = 8a = 120 \) см ⇒ \( a = 15 \) см. Площадь прямоугольника:
   \( 5a \cdot a = 5 \cdot 15 \cdot 15 = 1125 \) см².
   Ответ: 1125 см².
2. Всего 630 цветов: розы и гвоздики. Роз в 6 раз меньше. Стоимость всех роз — 24300 руб, что составляет треть общей стоимости. Определить, что дороже (роза или гвоздика) и на сколько рублей.
   Решение: Пусть количество роз — \( x \), тогда гвоздик — \( 6x \). Всего цветов:
   \( x + 6x = 630 \) ⇒ \( x = 90 \). Роз — 90, гвоздик —540. Цена розы:
   \( \frac{24300}{90} = 270 \) руб. Общая стоимость всех цветов:
   \( 24300 \cdot 3 = 72900 \) руб. Стоимость гвоздик:
   \( 72900 - 24300 = 48600 \) ⇒ цена гвоздики:
   \( \frac{48600}{540} = 90 \) руб. Разница:
   \( 270 - 90 = 180 \) руб.
   Ответ: Роза дороже гвоздики на 180 руб.
3. Вычислить: \( 50103-(405\cdot 709-381):138 \).
   Решение:
   \( 405 \cdot 709 = 287145 \),
   \( 287145 - 381 = 286764 \),
   \( 286764 : 138 = 2078 \),
   \( 50103 - 2078 = 48025 \).
   Ответ: 48025.
4. Петя вышел на 5 минут раньше Васи. При одновременном выходе встреча на равном расстоянии (1 км каждому). При раннем выходе Пети встреча в 800 м от Васиного дома. Сколько минут Пете идти до Васиного дома?
   Решение: Скорости одинаковы. Расстояние между домами — 2 км. Пусть время Васи до встречи \( t \) часов. Петя шел \( t + \frac{5}{60} = t + \frac{1}{12} \). Путь Пети:
   \( 2000 - 800 = 1200 \) м = 1,2 км. Уравнение:
   \( \frac{1,2}{t + \frac{1}{12}} = \frac{0,8}{t} \)
   Решение: \( t = \frac{1}{6} \) часа = 10 минут. Скорость Пети:
   \( \frac{1,2}{\frac{1}{6} + \frac{1}{12}} = 4,8 \) км/ч. Время до Васиного дома:
   \( \frac{2}{4,8} = \frac{5}{12} \) часа = 25 минут.
   Ответ: 25 минут.
5. Наименьшее шестизначное число с цифрами ≥7 не меньше, чем цифр <6.
   Решение: Минимальное число — 100777. Другие варианты содержат большие цифры или не удовлетворяют условию.
   Ответ: 100777.
6. Лиса съела часть сыра, осталось два квадратных ломтика с периметром втрое меньше исходного. Масса съеденного сыра.
   Решение: Сторона исходного сыра — \( a \). Площадь:
   \( a^2 = 72 \) г ⇒ \( a = \sqrt{72} \). Площадь маленьких кусков:
   \( 2 \cdot \left(\frac{a}{3}\right)^2 = \frac{2a^2}{9} \). Масса оставшегося сыра:
   \( \frac{2}{9} \cdot 72 = 16 \) г. Съедено:
   \( 72 - 16 = 56 \) г.
   Ответ: 56 г.
7. На 12-й полке книг в библиотеке, где любые три подряд полки содержат 80 книг.
   Решение: Количество книг на полках имеет периодичность \( a, b, c \). Полнкрып расписаны группы по три полки. Номер 12 соответствует третьей позиции в цикле, где всегда 17 книг.
   Ответ: 17.
8. Минимальная сумма серых клеток при нумерации с общими сторонами.
   Решение: Занумеровать таблицу так, чтобы серые клетки имели минимальные значения (1, 2, 3, 4). Их сумма:
   1 + 2 + 3 + 4 = 10. Пример маршрута:
   Ответ: Минимальная сумма — 10.