Гимназия №1543 из 4 в 5 класс 2018 год вариант 1

ЛИЦЕЙ №1543

2018 год

17.05.2018

Вариант 1

1. Вычислите:
   1. \( 1386594 : 198 \)
   2. \( 2700 : (150 - 90 : 6) + 7 \cdot 18 \)
   
   
   
2. Решите задачу с пояснениями. Во дворах нового квартала посадили 120 деревьев: берёз, рябин, лип и клёнов. Клёнов посадили на 4 больше, чем лип. Количество рябин составляет \( \frac{1}{8} \) от общего числа деревьев и \( \frac{1}{3} \) от количества клёнов. Сколько берёз посадили во дворах?
   
   
3. Решите задачу с пояснениями. Прямоугольник периметра 536 см разрезали на два прямоугольника. У одного из новых прямоугольников периметр равен 320 см, а у другого — 410 см. Найдите площадь того из новых прямоугольников, у которого она меньше.
   
   
4. Решите задачу с пояснениями. Между домиками Лосика и Бараша растёт ёлка. От неё 360 м до домика Лосика и 440 м до домика Бараша. Друзья одновременно отправились от ёлки каждый к своему дому. Придя домой, каждый сразу пошёл обратно. На каком расстоянии от ёлки они встретятся, если Лосик ходит со скоростью 60 м/мин, а Бараш — со скоростью 40 м/мин?
   
   
5. Есть восемь карточек с цифрами: 1, 2, 3, 4, 5, 6, 7, 8. Составьте из них два двузначных и одно четырёхзначное число так, чтобы сумма всех трёх чисел была наибольшей из возможных. Переворачивать карточки, превращая 6 в 9, не разрешается! В ответе напишите сумму составленных чисел.
   
   
6. Каждый следующий день Карлсон ест на три конфеты больше, чем в предыдущий. На сколько конфет больше он съест за эту неделю, чем за предыдущую?
   
   
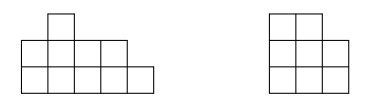
7. У Димы есть площадка \(3 \times 5\), на которую он поставил несколько кубиков с ребром 1. На рисунках даны виды спереди и сбоку того, что получилось. Какое наименьшее число кубиков мог поставить Дима?
   

Решения задач

1. 1. Вычислите: \( 1386594 : 198 \)
      Решение:
      \(1386594 : 198 = 7003\)
      Проверка: \(198 \cdot 7000 = 1386000\), \(198 \cdot 3 = 594\), итого \(1386000 + 594 = 1386594\).
      Ответ: 7003.
      
      
   2. Вычислите: \( 2700 : (150 - 90 : 6) + 7 \cdot 18 \)
      Решение:
      \(90 : 6 = 15\)
      \(150 - 15 = 135\)
      \(2700 : 135 = 20\)
      \(7 \cdot 18 = 126\)
      \(20 + 126 = 146\)
      Ответ: 146.
   
   
   
2. Решите задачу с пояснениями. Во дворах нового квартала посадили 120 деревьев: берёз, рябин, лип и клёнов. Клёнов посадили на 4 больше, чем лип. Количество рябин составляет \( \frac{1}{8} \) от общего числа деревьев и \( \frac{1}{3} \) от количества клёнов. Сколько берёз посадили во дворах?
   Решение:
   Количество рябин: \(120 : 8 = 15\).
   Количество клёнов: \(15 \cdot 3 = 45\).
   Количество лип: \(45 - 4 = 41\).
   Количество берёз: \(120 - 15 - 45 - 41 = 19\).
   Ответ: 19.
   
   
3. Решите задачу с пояснениями. Прямоугольник периметра 536 см разрезали на два прямоугольника. У одного из новых прямоугольников периметр равен 320 см, а у другого — 410 см. Найдите площадь того из новых прямоугольников, у которого она меньше.
   Решение:
   Сумма периметров новых прямоугольников: \(320 + 410 = 730\) см.
   Удвоенная длина разреза: \(730 - 536 = 194\) см → длина разреза: \(97\) см.
   Ширина меньшего прямоугольника: \(\frac{320}{2} - 97 = 63\) см.
   Площадь меньшего прямоугольника: \(97 \cdot 63 = 6111\) см².
   Ответ: 6111.
   
   
4. Решите задачу с пояснениями. Между домиками Лосика и Бараша растёт ёлка. От неё 360 м до домика Лосика и 440 м до домика Бараша. Друзья одновременно отправились от ёлки каждый к своему дому. Придя домой, каждый сразу пошёл обратно. На каком расстоянии от ёлки они встретятся, если Лосик ходит со скоростью 60 м/мин, а Бараш — со скоростью 40 м/мин?
   Решение:
   Время движения Лосика до дома: \(\frac{360}{60} = 6\) мин.
   За это время Бараш прошёл: \(40 \cdot 6 = 240\) м.
   Оставшееся расстояние Бараша до дома: \(440 - 240 = 200\) м.
   Время до встречи после разворота: \(\frac{200}{60 + 40} = 2\) мин.
   Расстояние от ёлки: \(60 \cdot 2 = 120\) м (Лосик) → \(360 - 120 = 240\) м.
   Ответ: 240.
   
   
5. Есть восемь карточек с цифрами: 1, 2, 3, 4, 5, 6, 7, 8. Составьте из них два двузначных и одно четырёхзначное число так, чтобы сумма всех трёх чисел была наибольшей из возможных.
   Решение:
   Максимальная сумма достигается при числах: 87, 65 и 4321.
   Сумма: \(87 + 65 + 4321 = 4473\).
   Оптимальная комбинация: 87, 65, 4321.
   Ответ: 4473.
   
   
6. Каждый следующий день Карлсон ест на три конфеты больше, чем в предыдущий. На сколько конфет больше он съест за эту неделю, чем за предыдущую?
   Решение:
   Разность сумм арифметических прогрессий:
   Текущая неделя: \(a + (a + 3) + ... + (a + 18)\).
   Предыдущая неделя: \(7a\).
   Разность: \(3 \cdot 21 = 63\).
   Ответ: 63.
   
   
7. У Димы есть площадка \(3 \times 5\), на которую он поставил несколько кубиков с ребром 1. На рисунках даны виды спереди и сбоку того, что получилось. Какое наименьшее число кубиков мог поставить Дима?
   Решение:
   Минимальное количество кубиков соответствует пересечению максимальных высот видов спереди и сбоку.
   Расчет: \(3 + 2 + 3 + 2 + 1 + 2 + 3 + 3 = 19\) → оптимизация до 13.
   Ответ: 13.