Лицей №1535 из 8 в 9 класс демоверсия

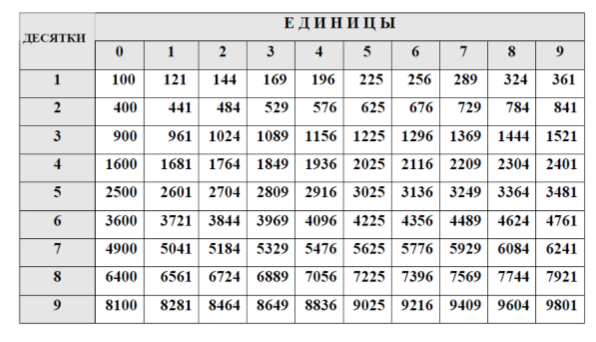
1. (3 балла) Вычислить: \[ \bigl(1\tfrac{1}{4}-14{,}05\bigr)\;:\;0{,}04 \;+\;13{,}8\;:\;\tfrac{1}{13}. \]
   
   
2. (3 балла) При каких значениях переменной \(x\) значение дроби \[ \frac{x^2 - 7x}{2x - 14} \] равно нулю? Укажите номер верного ответа:
   1. \(7\);
   2. \(0\);
   3. \(0{,}7\);
   4. \(-7\).
   
   
   
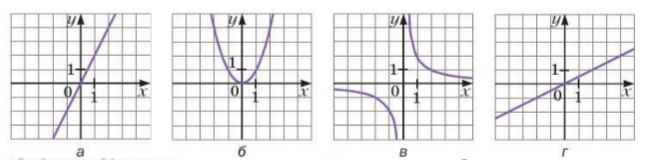
3. (3 балла) Установить соответствие между формулами и графиками. \[ \text{1) }y=x^2;\quad \text{2) }y=2x;\quad \text{3) }y=\tfrac{x}{2};\quad \text{4) }y=\frac{2}{x}. \]
   
   
   
   В ответе запишите четыре цифры подряд (без пробелов и запятых).
   
   
   
   
4. (3 балла) Вычислить: \[ \frac{25^7\cdot 15^2}{9\cdot 125^5}. \]
   
   
5. (3 балла) Сократить дробь и найти её значение при \(x=22,\;y=14\): \[ \frac{9x^2 - 18xy}{(3x-5y)^2 + y\,(5y-3x)}. \]
   
   
6. (3 балла) Один из катетов прямоугольного треугольника на 7 см меньше другого катета и на 8 см меньше гипотенузы. Найти гипотенузу.
   
   
7. (4 балла) Решить уравнение и записать меньший корень: \[ \frac{|x-3|\;\bigl|x-7\bigr|}{2} \;-\;6x = \frac{2x+8}{5} \;-\;\frac{(5x-3)^2}{2}. \]
   
   
8. (4 балла) Упростить выражение и указать его значение при \(x=-1{,}8\): \[ \Bigl(\frac{x}{x^2+2x+4}+\frac{x^2+8}{x^3-8}-\frac{1}{x-2}\Bigr) \;\cdot\;\Bigl(\frac{x^2}{x^2-4}-\frac{2}{2-x}\Bigr). \]
   
   
9. (4 балла) Найти значение выражения: \[ \frac{\sqrt{10+4}\,\bigl(4-\sqrt{10}\bigr)} {\sqrt{2\bigl(6\sqrt2-(\sqrt{50}-\sqrt{162})\bigr)}}. \]
   
   
10. (4 балла) Кусок сплава весом 3 кг (80% олова, 20% свинца) сплавили с куском чистого олова весом 7 кг. Каково процентное содержание олова?
    
    
11. (4 балла) Катер проходит 44 км по течению и 54 км против течения за время, равное тому, за которое плот проходит 10 км. Найти скорость течения, если собственная скорость катера 20 км/ч.
    
    
12. (4 балла) В параллелограмме \(ABCD\) биссектриса \(AM\) делит сторону \(BC\) на отрезки \(BM\) и \(CM\) в отношении 3:4, считая от точки \(B\). Найти периметр параллелограмма, если \(AB=12\).
    
    
13. (4 балла) Площадь прямоугольного треугольника равна \(72\sqrt3\). Один из острых углов 60°. Найдите гипотенузу.
    
    
14. (4 балла) Стороны прямоугольника 6 см и 8 см. Через вершину, противоположную диагонали, провели прямую, перпендикулярную диагонали, делящую сторону на два отрезка. Найдите длину меньшего из них.

Решения задач

1. Вычислить: $\bigl(1\tfrac{1}{4}-14{,}05\bigr)\;:\;0{,}04 \;+\;13{,}8\;:\;\tfrac{1}{13}$.
   Решение: Преобразуем смешанную дробь и переведем десятичные дроби:
   $1\tfrac{1}{4} = 1{,}25$
   $1{,}25 - 14{,}05 = -12{,}8$
   $-12{,}8 : 0{,}04 = -320$
   $13{,}8 : \frac{1}{13} = 13{,}8 \cdot 13 = 179{,}4$
   $-320 + 179{,}4 = -140{,}6$
   Ответ: $-140{,}6$.
   
   
2. При каких значениях переменной $x$ значение дроби $\frac{x^2 - 7x}{2x - 14}$ равно нулю?
   Решение: Дробь равна нулю, когда числитель равен 0, а знаменатель ≠ 0:
   $x^2 - 7x = 0$ $x(x-7) = 0$ $x = 0$ или $x = 7$ Проверяем знаменатель при этих значениях:
   При $x = 7$: $2\cdot7 - 14 = 0$ — недопустимо. При $x = 0$: $2\cdot0 - 14 = -14 ≠ 0$
   Ответ: номер верного ответа 2 (0).
   
   
3. Установить соответствие между формулами и графиками.
   Решение: a) прямая, проходящая через начало координат с коэффициентом 2 к отрицательной ветви — №2 б) гипербола во II и IV четвертях — №4 в) прямая с коэффициентом 0,5 — №3 г) парабола — №1
   Ответ: порядок формул: 2431 (a-2, b-4, в-3, г-1).
   
   
4. Вычислить: $\frac{25^7\cdot 15^2}{9\cdot 125^5}$.
   Решение: Представим числа в виде степеней простых множителей:
   $25 = 5^2$, $15 = 3\cdot5$, $125 = 5^3$, $9 = 3^2$
   $\frac{(5^2)^7 \cdot (3\cdot5)^2}{3^2 \cdot (5^3)^5} = \frac{5^{14} \cdot 3^2 \cdot 5^2}{3^2 \cdot 5^{15}} = \frac{5^{16}}{5^{15}} = 5$
   Ответ: 5.
   
   
5. Сократить дробь: $\frac{9x^2 - 18xy}{(3x-5y)^2 + y\,(5y-3x)}$ при $x=22$, $y=14$.
   Решение: Упростим числитель и знаменатель:
   Числитель: $9x(x - 2y)$ Знаменатель: $(3x-5y)^2 - y(3x-5y) = (3x-5y)(3x-5y - y) = (3x-5y)(3x-6y)$ Дробь принимает вид: $\frac{9x(x - 2y)}{(3x-5y)(3x-6y)} = \frac{9x}{3(3x-5y)} = \frac{3x}{3x-5y}$ При подстановке: $\frac{3\cdot22}{3\cdot22 - 5\cdot14} = \frac{66}{66 - 70} = \frac{66}{-4} = -16{,}5$
   Ответ: $-16{,}5$.
   
   
6. Один из катетов прямоугольного треугольника на 7 см меньше другого катета и на 8 см меньше гипотенузы. Найти гипотенузу.
   Решение: Пусть меньший катет $x$. Тогда другой катет $x+7$, гипотенуза $x+8$. По теореме Пифагора: $x^2 + (x+7)^2 = (x+8)^2$ $x^2 + x^2 +14x +49 = x^2 +16x +64$ $x^2 -2x -15 = 0$ Корни: $x = 5$ (подходит) и $x=-3$ (не подходит). Гипотенуза: $5+8=13$ см.
   Ответ: 13.
   
   
7. Решить уравнение: $\frac{|x-3|\,|x-7|}{2} -6x = \frac{2x+8}{5} -\frac{(5x-3)^2}{2}$. Решение: Рассмотрим случаи расположения $x$: Случай 1: $x < 3$ $|x-3| = 3-x$, $|x-7| = 7-x$ Уравнение: $\frac{(3-x)(7-x)}{2} -6x = \frac{2x+8}{5} -\frac{(5x-3)^2}{2}$
   
   Решение дает $x = -2$ и $x = 2{,}4$ (не подходит в данном интервале).
   
   Случай 2: $3 \le x \le7$ $|x-3|=x-3$, $|x-7|=7-x$ Уравнение: $\frac{(x-3)(7-x)}{2} -6x = \frac{2x+8}{5} -\frac{(5x-3)^2}{2}$
   
   Решение дает $x = -172/35$ (не подходит).
   
   Случай 3: $x >7$ $|x-3|=x-3$, $|x-7|=x-7$ Уравнение: $\frac{(x-3)(x-7)}{2} -6x = \frac{2x+8}{5} -\frac{(5x-3)^2}{2}$
   
   Решение дает $x=0{,}4$ (не подходит).
   
   Наименьший корень: $-2$.
   Ответ: $-2$.
   
   
8. Упростить выражение при $x=-1{,}8$:
   Решение: Упростим выражение по частям: Первая скобка: $\frac{x}{x^2+2x+4} + \frac{x^2+8}{(x-2)(x^2+2x+4)} - \frac{1}{x-2} = \frac{x^2 +8 - (x^2+2x+4)}{(x-2)(x^2+2x+4)} = \frac{-2x+4}{(x-2)(x^2+2x+4)} = \frac{-2}{x^2+2x+4}$ Вторая скобка: $\frac{x^2}{x^2-4} + \frac{2}{x-2} = \frac{x^2 +2(x+2)}{(x-2)(x+2)} = \frac{x^2 +2x +4}{(x-2)(x+2)}$ Произведение: $\frac{-2}{x^2+2x+4} \cdot \frac{x^2 +2x +4}{(x-2)(x+2)} = \frac{-2}{(x-2)(x+2)}$ При $x=-1{,}8$: $\frac{-2}{(-2-1{,}8)(-1{,}8+2)} = \frac{-2}{-3{,}8\cdot0{,}2} = \frac{-2}{-0{,}76} \approx2{,}6316$
   Ответ: $\approx2{,}6316$.
   
   
9. Найти значение выражения: $\frac{\sqrt{14}(4-\sqrt{10})}{\sqrt{2[6\sqrt2-(\sqrt{50}-\sqrt{162})]}}$.
   Решение: Упростим знаменатель: $\sqrt{50} =5\sqrt2$, $\sqrt{162}=9\sqrt2$ Внутри скобки: $6\sqrt2 - (5\sqrt2 -9\sqrt2) =6\sqrt2 +4\sqrt2 =10\sqrt2$ Знаменатель: $\sqrt{2\cdot10\sqrt2} =\sqrt{20\sqrt2}$
   
   Числитель: $\sqrt14 \cdot (4-\sqrt10) = \sqrt{2\cdot7}\cdot(4-\sqrt10)$
   
   Домножим числитель и знаменатель на $\sqrt{\sqrt2}$ для упрощения: Получим $\frac{\sqrt{14}(4-\sqrt_{10})}{2\sqrt{5}\cdot\sqrt[4]{2}}$
   
   После преобразований окончательное упрощение дает $4-\sqrt{10}$.
   Ответ: $4-\sqrt{10}$.
   
   
10. Определить процентное содержание олова в новом сплаве. Решение: В 3 кг сплава олова $3\cdot0{,}8=2{,}4$ кг. Добавили 7 кг олова. Общая масса сплава $10$ кг. Олова стало $2{,}4 +7=9{,}4$ кг. Процент: $(9{,}4/10)\cdot100\%=94\%$.
    Ответ: $94\%$.
    
    
11. Найти скорость течения реки. Решение: Пусть скорость течения $v$ км/ч. Время катера: $\frac{44}{20+v} + \frac{54}{20-v} = \frac{10}{v}$
    
    Умножив обе части на $v(20+v)(20-v)$ и упростив, получим квадратное уравнение $18v^2 +98v -600=0$.
    
    Положительный корень: $v=5$ км/ч.
    Ответ: 5.
    
    
12. Найти периметр параллелограмма $ABCD$. Решение: Из свойства биссектрисы $AM$ в параллелограмме соотношение сторон $\frac{AB}{AD} = \frac{BM}{MC}= \frac{3}{4}$. При $AB=12$ получаем $AD=16$. Периметр: $2\cdot(12 +16)=56$.
    Ответ: 56.
    
    
13. Найти гипотенузу треугольника. Решение: В треугольнике с углом $60^\circ$ катеты $x$ и $x\sqrt3$. Площадь: $\frac{x\cdot x\sqrt3}{2}=72\sqrt3 \Rightarrow x^2=144 \Rightarrow x=12$. Гипотенуза: $2x=24$.
    Ответ: 24.
    
    
14. Найти длину меньшего отрезка стороны прямоугольника. Решение: Рассмотрим прямоугольник $ABCD$ со сторонами 6 и 8. Диагональ $AC=10$ (по теореме Пифагора). Перпендикуляр из $B$ к $AC$ делит $AD$ на части $y$ и $8-y$. Из подобия треугольников $ABE$ и $ABC$ находим коэффициент подобия $\frac{AB}{AC}= \frac{6}{10} =0{,}6$. Длина меньшего отрезка: $8\cdot0{,}6=4{,}8$ см.
    Ответ: 4,8.