Лицей №1535 из 6 в 7 класс

1. (1 балл) Вычислите: \[ -84 - 13\cdot(-5). \]
2. (1 балл) Вычислите: \[ 1 - \frac{4}{7} : \frac{16}{21}. \]
3. (1 балл) Вычислите: \[ (-7{,}1 + 2{,}7)\cdot 0{,}8. \]
4. (2 балла) Чему равен остаток от деления числа 195 на число 14?
5. (2 балла) Чему равно значение выражения \[ 29 : 2\frac{3}{13} - 13{,}6 + 1? \]
6. (3 балла) Чему равно значение выражения \[ \bigl|-3 + |2a - 2|\bigr|, \quad\text{если }a = -1{,}5? \]
7. (2 балла) Найдите число, 22% которого равны 110.
8. (3 балла) При каком значении \(x\) разность значений выражений \(8(x-7)\) и \(6(x-4)\) равна 10?
9. (3 балла) Даны числа: \[ -\tfrac{13}{7},\quad -\tfrac{9}{7},\quad \tfrac{20}{7},\quad -\tfrac{20}{7},\quad -\tfrac{15}{7}. \] Три из них отмечены на числовой оси точками \(A\), \(B\) и \(C\). Установите соответствие: \[ \text{A)}\;A\quad\text{Б)}\;B\quad\text{В)}\;C \quad\longleftrightarrow\quad 1)\!-\tfrac{13}{7},\;2)\!-\tfrac{9}{7},\;3)\tfrac{20}{7},\;4)\!-\tfrac{20}{7},\;5)\!-\tfrac{15}{7}. \] В ответе запишите три цифры без пробелов.
   
   
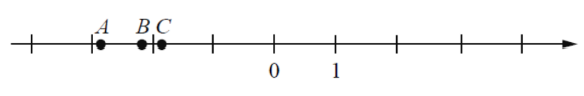
10. (3 балла) Два трактора вспахали поле за 5 ч. Сколько надо тракторов, чтобы вспахать такое же поле за 2 ч?
11. (3 балла) Длина прямоугольника 72 мм. Ширина составляет \(\tfrac{8}{9}\) длины. Чему равен периметр в сантиметрах?
12. (3 балла) Скорость течения реки $2{,}9$ км/ч. Катер за 5 ч прошёл против течения $35{,}5$ км. Какова собственная скорость катера в км/ч?
13. (4 балла) Расстояние между двумя городами на карте равно $3{,}2$ см, масштаб 1:16 000 000. Сколько км между городами на местности?
14. (4 балла) При каком \(x\) верно равенство \[ \frac{x+1}{3} = \tfrac{1}{3} : 0{,}2? \]
15. (5 баллов) Длины сторон треугольника относятся как \(3:4:5\). Найдите периметр (в см), если разность наибольшей и наименьшей сторон равна 18 см.
16. (5 баллов) Путешественник в первый день прошёл 15% всего пути, во второй — \(\tfrac{2}{7}\) всего пути. Сколько км он прошёл во второй день, если в первый он прошёл 21 км?
17. (5 баллов) Для получения томатной пасты протёртую массу томатов выпаривают до 30% воды. Сколько т пасты получится из 28 т протёртой массы, содержащей 95% воды?

Решения задач

1. Вычислите: \[ -84 - 13\cdot(-5) \] Решение: \[ -84 -13 \cdot (-5) = -84 + 65 = -19 \] Ответ: $-19$.
2. Вычислите: \[ 1 - \frac{4}{7} : \frac{16}{21} \] Решение: \[ 1 - \frac{4}{7} \cdot \frac{21}{16} = 1 - \frac{3}{4} = \frac{1}{4} = 0{,}25 \] Ответ: $0{,}25$.
3. Вычислите: \[ (-7{,}1 + 2{,}7)\cdot 0{,}8 \] Решение: \[ (-4{,}4) \cdot 0{,}8 = -3{,}52 \] Ответ: $-3{,}52$.
4. Чему равен остаток от деления числа 195 на число 14? $\newline$ Решение: Наибольшее число, кратное 14 и не превышающее 195: $14 \cdot 13 = 182$. Остаток: $195 - 182 = 13$. $\newline$ Ответ: $13$.
5. Чему равно значение выражения \[ 29 : 2\frac{3}{13} - 13{,}6 + 1? \] Решение: \[ 29 : \frac{29}{13} = 29 \cdot \frac{13}{29} = 13 \] \[ 13 - 13{,}6 + 1 = -0{,}6 + 1 = 0{,}4 \] Ответ: $0{,}4$.
6. Чему равно значение выражения \[ \bigl|-3 + |2a - 2|\bigr|, \quad\text{если }a = -1{,}5? \] Решение: \[ 2 \cdot (-1{,}5) - 2 = -3 - 2 = -5 \] \[ |-5| = 5 \] \[ |-3 + 5| = |2| = 2 \] Ответ: $2$.
7. Найдите число, 22% которого равны 110. $\newline$ Решение: \[ x = \frac{110}{0{,}22} = 500 \] Ответ: $500$.
8. При каком значении \(x\) разность значений выражений \(8(x-7)\) и \(6(x-4)\) равна 10? $\newline$ Решение: \[ 8(x - 7) - 6(x - 4) = 10 \] \[ 8x - 56 -6x +24 = 10 \] \[ 2x -32 =10 \implies 2x =42 \implies x =21 \] Ответ: $21$.
9. Даны числа: \[ -\tfrac{13}{7},\quad -\tfrac{9}{7},\quad \tfrac{20}{7},\quad -\tfrac{20}{7},\quad -\tfrac{15}{7}. \] Три из них отмечены на числовой оси точками \(A\), \(B\) и \(C\). Установите соответствие: $\newline$ Решение: Числа расположены на оси слева направо: $- \frac{20}{7}$ (C)$, -\frac{15}{7}$ (B)$, -\frac{13}{7}$ (A). $\newline$ Ответ: $154$ (A — 1, B — 5, C — 4).
10. Два трактора вспахали поле за 5 ч. Сколько надо тракторов, чтобы вспахать такое же поле за 2 ч? $\newline$ Решение: Объем работы $= 2 \cdot 5 =10$ тракторо-часов. Для времени 2 часа: $N = \frac{10}{2}=5$. $\newline$ Ответ: $5$.
11. Длина прямоугольника 72 мм. Ширина составляет $\tfrac{8}{9}$ длины. Чему равен периметр в сантиметрах? $\newline$ Решение: Ширина $=72 \cdot \frac{8}{9} =64$ мм. Периметр $=2 \cdot (72 + 64) =272$ мм $=27{,}2$ см. $\newline$ Ответ: $27{,}2$ см.
12. Скорость течения реки $2{,}$9 км/ч. Катер за 5 ч прошёл против течения $35{,}5$ км. Какова собственная скорость катера в км/ч? $\newline$ Решение: \[ (V -2{,}9) \cdot 5 =35{,}5 \implies V -2{,}9 =7{,}1 \implies V=10 \] Ответ: $10$.
13. Расстояние между двумя городами на карте равно $3{,}2$ см, масштаб 1:16 000 000. Сколько км между городами на местности? $\newline$ Решение: \[ 3{,}2 \cdot 16 000 000 =51 200 000 \text{ см} =512 \text{ км} \] Ответ: $512$.
14. При каком \(x\) верно равенство \[ \frac{x+1}{3} = \tfrac{1}{3} : 0{,}2? \] Решение: \[ \frac{1}{3} : 0{,}2 = \frac{1}{3} \cdot 5 = \frac{5}{3} \] \[ x +1 =5 \implies x =4 \] Ответ: $4$.
15. Длины сторон треугольника относятся как $3:4:5$. Найдите периметр (в см), если разность наибольшей и наименьшей сторон равна 18 см. $\newline$ Решение: Коэффициент пропорции $k$: \[ 5k -3k =2k=18 \implies k=9 \] Периметр $= (3+4+5) \cdot9 =108$ см. $\newline$ Ответ: $108$.
16. Путешественник в первый день прошёл 15% всего пути, во второй — $\tfrac{2}{7}$ всего пути. Сколько км он прошёл во второй день, если в первый он прошёл 21 км? $\newline$ Решение: Весь путь: \[ 21 : 0{,}15 =140 \text{ км} \] Во второй день: \[ 140 \cdot \tfrac{2}{7} =40 \text{ км} \] Ответ: $40$.
17. Для получения томатной пасты протёртую массу томатов выпаривают до 30% воды. Сколько т пасты получится из 28 т протёртой массы, содержащей 95% воды? $\newline$ Решение: Сухое вещество: \[ 28 \cdot (1 -0{,}95) =1{,}4 \text{ т} \] Новая масса пасты: \[ 1{,}4 : (1 -0{,}3) =2 \text{ т} \] Ответ: $2$.