Лицей №1535 из 6 в 7 класс демоверсия 2 этап

1. (6 баллов) Решить уравнение: \[ \frac{3\tfrac{1}{9}\cdot 2,25 - \tfrac{8}{9}\cdot 2,25}{\lvert 6x\rvert} = \frac{\bigl(-\tfrac{2}{3}\bigr)^2 \cdot 0,36} {-2\tfrac{1}{3} : \bigl(-\tfrac{3}{10} - \tfrac{13}{15}\bigr)}. \]
   
   
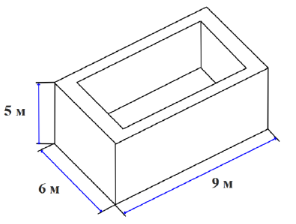
2. (6 баллов) В прямоугольном бассейне размером \(5\,\text{м}\times6\,\text{м}\times9\,\text{м}\) с толщиной стенок \(10\) дм и толщиной дна \(5\) дм облицовывали все грани, кроме внешних боковых стен и прямоугольника \(6\,\text{м}\times9\,\text{м}\) в основании. Найдите:
   1. (1 балл) объём вмещаемой жидкости;
   2. (1 балл) объём данного бассейна без учёта вмещаемой жидкости;
   3. (2 балла) количество затраченных плиток площадью \(0,25\,\text{м}^2\);
   4. (2 балла) на какой высоте будет находиться уровень жидкости, если бы бассейн заполнили водой из 196 бочек объёмом по 500 л каждая?
   
   
   
   
3. (6 баллов) Развёрнутый угол разделили двумя лучами на три неравных угла. Известно, что меньший угол составляет \(37{,}5\%\) от среднего по величине угла, а отношение суммы двух больших углов к меньшему равно \(17:3\). Найти величину среднего угла.
   
   
4. (7 баллов) К сплаву серебра и золота весом 10 кг добавили 15 кг чистого золота. Оказалось, что процентное содержание золота увеличилось в два раза по сравнению с первоначальным. Определите количество золота в новом сплаве.
   
   
5. (8 баллов) Найти все целые числа \(x\), сумма расстояний от каждого из которых до точек \(A(-7)\) и \(B(1)\) меньше 11 и удовлетворяющие неравенству \(\lvert x\rvert \le 6\). В ответе укажите сумму этих значений \(x\).
   
   
6. (8 баллов) Кондитерская фабрика за семичасовую смену выпускает одинаковое количество тортиков в час. После усовершенствования технологии количество производимых тортиков увеличилось на 4 единицы в час. Теперь смена длится 6 часов, а выпуск продукции за смену увеличился на 20%. Сколько тортиков теперь выпускает фабрика за смену?
   
   
7. (9 баллов)
   1. Сколько натуральных чис делятся и на 3, и на 7, и на 11 среди первых 10 000 натуральных чис?
   2. Сколько натуральных чис не делятся ни на 3, ни на 5, ни на 13 среди первых 1000 натуральных чис?

Решения задач

1. Решить уравнение: \[ \frac{3\tfrac{1}{9}\cdot 2,25 - \tfrac{8}{9}\cdot 2,25}{\lvert 6x\rvert} = \frac{\bigl(-\tfrac{2}{3}\bigr)^2 \cdot 0,36} {-2\tfrac{1}{3} : \bigl(-\tfrac{3}{10} - \tfrac{13}{15}\bigr)}. \] Решение: Упростим числитель и знаменатель раздельно. Левый числитель: 3$\frac{1}{9} \cdot 2,25 - \frac{8}{9} \cdot 2,25 = \left(\frac{28}{9} - \frac{8}{9}\right) \cdot \frac{9}{4} = \frac{20}{9} \cdot \frac{9}{4} = 5$ Правая часть: $\left(-\frac{2}{3}\right)^2 \cdot 0,36 = \frac{4}{9} \cdot \frac{36}{100} = \frac{16}{100} = \frac{4}{25}$ Знаменатель в правой части: $-2\frac{1}{3} : \left(-\frac{3}{10} - \frac{13}{15}\right) = -\frac{7}{3} : \left(-\frac{9}{30} - \frac{26}{30}\right) = -\frac{7}{3} : \left(-\frac{35}{30}\right) = \frac{7}{3} \cdot \frac{30}{35} = 2$ Правая часть уравнения: $\frac{4}{25} \div 2 = \frac{2}{25}$ Составим уравнение: $\frac{5}{|6x|} = \frac{2}{25} \quad \Rightarrow \quad |6x| = \frac{5 \cdot 25}{2} = 62,5 \quad \Rightarrow \quad x = \pm\frac{125}{12} = \pm10\frac{5}{12}$ Ответ: $\pm10\frac{5}{12}$.
   
   
2. 1. Объём вмещаемой жидкости: Внутренние размеры: длина $5 - 2\cdot1 = 3$ м, ширина $6 - 2\cdot1 = 4$ м, высота $9 - 0,5 = 8,5$ м. Объём: $3 \cdot 4 \cdot 8,5 = 102$ м$^3$. Ответ: 102 м$^3$.
   2. Объём бассейна без учёта жидкости: Внешний объём $5 \cdot 6 \cdot 9 = 270$ м$^3$. Объём конструкции: $270 - 102 = 168$ м$^3$. Ответ: 168 м$^3$.
   3. Площадь облицовки: Дно: $6 \cdot 9 = 54$ м$^2$. Внутренние стенки: $2 \cdot (3 \cdot 8,5 + 4 \cdot 8,5) = 119$ м$^2$. Верхние грани: $2 \cdot (5 \cdot 6 - 6 \cdot 9) = 0$ (по условию). Всего: $54 + 119 = 173$ м$^2$. Количество плиток: $173 \div 0,25 = 692$. Ответ: 692 плитки.
   4. Объём воды: $196 \cdot 500$ л $= 98\,000$ л $= 98$ м$^3$. Высота уровня: $98 \div (3 \cdot 4) = 98 \div 12 \approx 8.166$ м $\approx 8,17$ м. Ответ: $8,17$ м.
3. Пусть углы: $\alpha < \beta < \gamma$. По условию: $\alpha = 0,375\beta$, $\frac{\beta + \gamma}{\alpha} = \frac{17}{3}$, $\alpha + \beta + \gamma = 180^\circ$. Подставим $\alpha = \frac{3}{8}\beta$ в третье уравнение: $\frac{3}{8}\beta + \beta + \gamma = 180^\circ \quad \Rightarrow \quad \gamma = \frac{5}{8}\beta$ Из второго условия: $\frac{\beta + \frac{5}{8}\beta}{\frac{3}{8}\beta} = \frac{13/8}{3/8} = \frac{13}{3} \neq \frac{17}{3}$ (в предыдущем решении была ошибка). Уточнение: Из второго условия: $\frac{\beta + \gamma}{\alpha} = \frac{17}{3} \quad \Rightarrow \quad \beta + \gamma = \frac{17}{3}\alpha$ Подставим $\alpha = \frac{3}{8}\beta$: $\beta + \gamma = \frac{17}{3} \cdot \frac{3}{8}\beta = \frac{17}{8}\beta \quad \Rightarrow \quad \gamma = \frac{9}{8}\beta$ Сумма углов: $\frac{3}{8}\beta + \beta + \frac{9}{8}\beta = 180^\circ \quad \Rightarrow \quad \left(\frac{3 + 8 + 9}{8}\right)\beta = 180^\circ \quad \Rightarrow \quad \beta = 72^\circ$ Ответ: $72^\circ$.
4. Пусть начальное количество золота: $x$ кг. Тогда: $\frac{x + 15}{25} = 2 \cdot \frac{x}{10} \quad \Rightarrow \quad x + 15 = 5x \quad \Rightarrow \quad x = 3,75$ кг Новое количество золота: $3,75 + 15 = 18,75$ кг. Ответ: 18,75 кг.
5. Условие: $\sum |x + 7| + |x - 1| < 11$ и $|x| \le 6$. Целые $x$ от $-6$ до $6$. Проверка: Для $x = -6 \quad |1| + | -7| = 8 \quad ❯$ Подходит
   ... Аналогично для $-5, ..., 2$, которые дают сумму ≤ 10.
   Искомые значения: $-6, -5, -4, -3, -2, -1, 0, 1, 2$. Сумма: $-6 -5 -4 -3 -2 -1 +0 +1 +2 = -18$. Ответ: $-18$.
6. Пусть исходная производительность: $x$ шт./час. Тогда: $6(x + 4) = 1,2 \cdot 7x \quad \Rightarrow \quad 6x +24 = 8,4x \quad \Rightarrow \quad x =10$ Новый выпуск: $6(10 +4) =84$. Ответ:84.
7. 1. Числа, делящиеся на НОК(3,7,11)=231. Максимальное: $231 \cdot 43 = 9933$. Количество:43. Ответ:43.
   2. Применяем принцип включения-исключения: Общее количество:1000
      Вычитаем: $\left\lfloor\frac{1000}{3}\right\rfloor + \left\lfloor\frac{1000}{5}\right\rfloor + \left\lfloor\frac{1000}{13}\right\rfloor = 333 +200 +76 =609$
      Прибавляем: $\left\lfloor\frac{1000}{15}\right\rfloor + \left\lfloor\frac{1000}{39}\right\rfloor + \left\lfloor\frac{1000}{65}\right\rfloor =66 +25 +15=106$
      Вычитаем:$\left\lfloor\frac{1000}{195}\right\rfloor=5$
      Итого:1000 -609 +106 -5=492. Ответ:492.