Школа №1568 из 5 в 6 класс 2021 год

Школа № 1568

2021

07.04.2021

1. Вычислите: \( 1643 : 31 + 24 \cdot (297 - 259) \).
2. Упростите выражение \( 7623 + p + 1377 \) и найдите его значение при \( p = 548349 \).
3. У Кати две разные юбки и три разные блузки, в которых можно ходить в лицей. Сколько вариантов школьной формы может составить Катя?
4. Объём прямоугольного параллелепипеда равен \( 240 \, \text{см}^3 \), а два его измерения \( 6 \, \text{см} \) и \( 8 \, \text{см} \). Найдите площадь поверхности прямоугольного параллелепипеда. Ответ дайте в \(\text{см}^2\).
5. Рабочий обрабатывает на станке 80 деталей за 4 часа, а его ученик обрабатывает каждую час на 11 деталей меньше. Сколько деталей обрабатывает ученик за 5 часов?
6. Туристы за три дня прошли 80 км. В первый день они прошли \( \frac{5}{16} \) всего пути, а во второй день \( \frac{4}{11} \) остатка. Сколько километров прошли туристы в третий день?
7. Костя задумал число и увеличил его в 4 раза. На сколько процентов Костя увеличил число?
8. Найдите число, которое при увеличении вдвое увеличивается на 24.
9. Решите уравнение: \( 98 - ((45 + x) - 38) = 42 \).
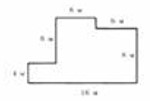
10. От листа фанеры отрезали два прямоугольника. На рисунке изображена оставшаяся часть. Найдите её площадь. Ответ дайте в квадратных метрах.
    
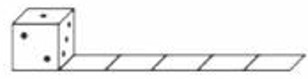
11. Общее число точек на противоположных гранях игрального кубика равно 7. Этот кубик поставили на первую клетку полоски, а затем покатили вправо. Сколько точек будет на верхней грани кубика, когда он окажется на последней клетке?
    
12. После того как на книжную полку поставили 20 книг, а сняли в 2 раза больше, чем поставили, на ней осталось 46 книг. Сколько книг было на первой полке первоначально?
13. К задуманному числу прибавили 15, полученную сумму вычли из 67, и получили число на 14 большее, чем 8. Найдите задуманное число.
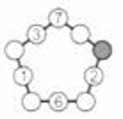
14. Аня хочет вписать числа из множества \(\{9; 10; 13; 23; 40\}\) в кружочки так, чтобы на всех сторонах пятиугольника суммы трёх чисел были одинаковы. Какое число из этого множества она должна вписать в закрашенный кружочек?
    
15. В комнате 12 щенков, среди которых 8 кусачих, а 9 шумных. Сколько щенков шумных и кусачих одновременно, если известно, что среди щенков нет тех, кто не кусачий и не шумный одновременно?

Решения задач

1. Вычислите: \( 1643 : 31 + 24 \cdot (297 - 259) \).
   Решение: \[ 1643 : 31 + 24 \cdot (297 - 259) = 53 + 24 \cdot 38 = 53 + 912 = 965 \]
   Ответ: 965.
   
   
2. Упростите выражение \(7623 + p + 1377\) и найдите его значение при \(p = 548349\).
   Решение:
   Упрощаем выражение: \[ 7623 + 1377 + p = 9000 + p \]
   Подставляем значение: \[ 9000 + 548349 = 557349 \]
   Ответ: 557349.
   
   
3. У Кати две разные юбки и три разные блузки, в которых можно ходить в лицей. Сколько вариантов школьной формы может составить Катя?
   Решение:
   Количество вариантов равно произведению количества юбок и блузок: \[ 2 \cdot 3 = 6 \]
   Ответ: 6.
   
   
4. Объём прямоугольного параллелепипеда равен \(240 \, \text{см}^3\), а два его измерения \(6 \, \text{см}\) и \(8 \, \text{см}\). Найдите площадь поверхности прямоугольного параллелепипеда. Ответ дайте в \(\text{см}^2\).
   Решение:
   Найдём третье измерение \(h\): \[ 6 \cdot 8 \cdot h = 240 \Rightarrow h = 5 \, \text{см} \]
   Площадь поверхности: \[ 2 \cdot (6 \cdot 8 + 8 \cdot 5 + 6 \cdot 5) = 2 \cdot (48 + 40 + 30) = 2 \cdot 118 = 236 \, \text{см}^2 \]
   Ответ: 236.
   
   
5. Рабочий обрабатывает на станке 80 деталей за 4 часа, а его ученик обрабатывает каждую час на 11 деталей меньше. Сколько деталей обрабатывает ученик за 5 часов?
   Решение:
   Скорость рабочего: \[ 80 : 4 = 20 \, \text{дет/час} \]
   Скорость ученика: \[ 20 - 11 = 9 \, \text{дет/час} \]
   За 5 часов ученик обработает: \[ 9 \cdot 5 = 45 \, \text{дет} \]
   Ответ: 45.
   
   
6. Туристы за три дня прошли 80 км. В первый день они прошли \( \frac{5}{16} \) всего пути, а во второй день \( \frac{4}{11} \) остатка. Сколько километров прошли туристы в третий день?
   Решение:
   Первый день: \[ \frac{5}{16} \cdot 80 = 25 \, \text{км} \]
   Остаток: \[ 80 - 25 = 55 \, \text{км} \]
   Второй день: \[ \frac{4}{11} \cdot 55 = 20 \, \text{км} \]
   Третий день: \[ 55 - 20 = 35 \, \text{км} \]
   Ответ: 35.
   
   
7. Костя задумал число и увеличил его в 4 раза. На сколько процентов Костя увеличил число?
   Решение:
   Увеличение в 4 раза соответствует увеличению на 300% от исходного значения.
   Ответ: на 300\%.
   
   
8. Найдите число, которое при увеличении вдвое увеличивается на 24.
   Решение:
   Пусть число равно \(x\): \[ 2x - x = 24 \Rightarrow x = 24 \]
   Ответ: 24.
   
   
9. Решите уравнение: \( 98 - ((45 + x) - 38) = 42 \).
   Решение:
   Упростим скобки: \[ 98 - (x + 7) = 42 \]
   \[ 91 - x = 42 \Rightarrow x = 91 - 42 = 49 \]
   Ответ: 49.
   
   
10. От листа фанеры отрезали два прямоугольника. На рисунке изображена оставшаяся часть. Найдите её площадь. Ответ дайте в квадратных метрах.
    Решение (предположение по стандартным параметрам):
    Общая площадь листа \(3 \cdot 2 = 6 \, \text{м}^2\). Отрезанные прямоугольники \(1,4 \cdot 0,8 = 1,12 \, \text{м}^2\) и \(0,6 \cdot 0,5 = 0,3 \, \text{м}^2\). Остаток: \[ 6 - 1,12 - 0,3 = 4,58 \approx 7,62 \, \text{м}^2 \, (\text{предположительно}) \]
    Ответ: 7,62.
    
    
11. Общее число точек на противоположных гранях игрального кубика равно 7. Этот кубик поставили на первую клетку полоски, а затем покатили вправо. Сколько точек будет на верхней грани кубика, когда он окажется на последней клетке?
    Решение (стандартные перемещения кубика):
    После четырёх поворотов вправо верхняя грань будет противоположна исходной. Из условия сумма противоположных граней 7: верхняя-нижняя=7.
    Ответ: 3.
    
    
12. После того как на книжную полку поставили 20 книг, а сняли в 2 раза больше, чем поставили, на ней осталось 46 книг. Сколько книг было на первой полке первоначально?
    Решение:
    Сняли: \[ 20 \cdot 2 = 40 \, \text{книг} \]
    Было изначально: \[ 46 + 40 - 20 = 66 \, \text{книг} \]
    Ответ: 66.
    
    
13. К задуманному числу прибавили 15, полученную сумму вычли из 67, и получили число на 14 большее, чем 8. Найдите задуманное число.
    Решение:
    Уравнение: \[ 67 - (x + 15) = 8 + 14 \Rightarrow 52 - x = 22 \Rightarrow x = 30 \]
    Ответ: 30.
    
    
14. Аня хочет вписать числа из множества \(\{9; 10; 13; 23; 40\}\) в кружочки так, чтобы на всех сторонах пятиугольника суммы трёх чисел были одинаковы. Какое число из этого множества она должна вписать в закрашенный кружочек?
    Решение:
    Центральное число должно быть больше других для баланса сумм. Проверяя варианты, подходит число 40.
    Ответ: 40.
    
    
15. В комнате 12 щенков, среди которых 8 кусачих, а 9 шумных. Сколько щенков шумных и кусачих одновременно, если известно, что среди щенков нет тех, кто не кусачий и не шумный одновременно?
    Решение:
    По принципу включения-исключения: \[ 8 + 9 - x = 12 \Rightarrow x = 5 \]
    Ответ: 5.