Лицей №239 из 8 в 9 класс 2012 год (вариант 2)

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ № 239

2012 год

1. $x_{1}$ меньший корень уравнения $3 x^{2}+2 x-7=0$. Вычислите $6 x_{1}^{2}+4 x_{1}-11$.
2. Вычислить: $\frac{2,4}{0,08}+\frac{0,21}{0,07}+\frac{4}{0,4}$
3. Решить в целых числах $x \cdot(y-4)=3$, если известно, что $x<0$
4. Решить уравнение: $(2-x)^{3}+x^{3}=2$
5. Решить неравенство: $\frac{(x-2)^{2} \cdot(x+2) \cdot(x-4)}{\sqrt{x+1}} \geq 0$.
6. Если $x^{2}-8 x-3=(x+a)^{2}+b$, то чему равно значение $b$ ?
7. $x_{1}$ и $x_{2}$ корни уравнения $x^{2}-p x+10=0$. Решить уравнение, если $x_{1}^{2}+x_{2}^{2}=29$.
8. Велосипедист проехал за 1,5 часа 36 км, а за следующие 2 часа еще 34 км. Найдите среднюю скорость велосипедиста
9. Построить график $|y|=|x-1|$.
10. Решить уравнение: $\left|x^{2}+4 x\right|=x^{2}-x-5$.
11. Решить уравнение: $\left|x^{2}+4 x\right|=x^{2}-x-5$.
12. Сравнить числа $a=3+2 \sqrt{5}$ и $b=\sqrt{14}+\sqrt{15}$
13. При каких значениях $a$ уравнение $4 x^{3}+4 x^{2}+a x=0$ имеет два различных корня?
14. При каких значениях $a$ система $\left\{\begin{array}{l}y=x^{2}+4 x+3 \\ y=a\end{array}\right.$ имеет единственное решение?
15. Из Петербурга в Москву можно проехать двумя способами, а из Москвы в Хабаровск пятью способами. Сколькими способами можно проехать их Петербурга в Хабаровск?
16. Найдите координаты точки, через которую проходят все прямые вида $y+2=\kappa x+\kappa$
17. Диагонали ромба 16 см и 11 см. Найдите его площадь.
18. Около прямоугольного треугольника $A B C$ с прямым углом $C$ описана окружность. Найдите радиус этой окружности, если $B C=12 \mathrm{~cm}, \angle A=30^{\circ}$.
19. В прямоугольном треугольнике угол $C$ прямой, $\sin \angle A=\frac{2}{3}$. Найдите тангенс этого угла.
20. В равнобедренном треугольнике угол между высотами, проведѐнными на боковые стороны равен $80^{\circ} .$ Найдите угол при вершине треугольника.
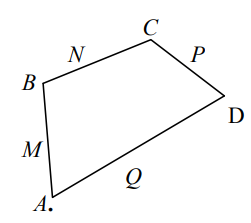
21. В четырехугольнике $A B C D$ точки $M, N . P, Q$ - середины сторон. Найдите площадь четырехугольника $A B C D$, если площадь четырехугольника $M N P Q$ равна $S$.
    

Решения задач

1. $x_{1}$ — меньший корень уравнения $3 x^{2}+2 x-7=0$. Вычислите $6 x_{1}^{2}+4 x_{1}-11$.
   Решение: Поскольку $x_{1}$ — корень уравнения, $3x_{1}^{2} + 2x_{1} - 7 = 0$. Умножим обе части на 2:
   $6x_{1}^{2} + 4x_{1} = 14$. Тогда:
   $6x_{1}^{2} + 4x_{1} - 11 = 14 - 11 = 3$.
   Ответ: 3.
   
   
2. Вычислить: $\frac{2,4}{0,08}+\frac{0,21}{0,07}+\frac{4}{0,4}$.
   Решение:
   $\frac{2,4}{0,08} = 30$; $\frac{0,21}{0,07} = 3$; $\frac{4}{0,4} = 10$.
   Сумма: $30 + 3 + 10 = 43$.
   Ответ: 43.
   
   
3. Решить в целых числах $x \cdot(y-4)=3$, если известно, что $x<0$.
   Решение: Целые делители 3: $\pm1$, $\pm3$. Учитывая $x < 0$:
   $x = -1$: $y - 4 = -3 \Rightarrow y = 1$.
   $x = -3$: $y - 4 = -1 \Rightarrow y = 3$.
   Ответ: $(-1, 1)$, $(-3, 3)$.
   
   
4. Решить уравнение: $(2-x)^{3}+x^{3}=2$.
   Решение: Раскроем кубы:
   $(8 - 12x + 6x^{2} - x^{3}) + x^{3} = 2$.
   Упростим: $6x^{2} - 12x + 6 = 0 \Rightarrow x^{2} - 2x + 1 = 0 \Rightarrow (x - 1)^{2} = 0$.
   Ответ: 1.
   
   
5. Решить неравенство: $\frac{(x-2)^{2} \cdot(x+2) \cdot(x-4)}{\sqrt{x+1}} \geq 0$.
   Решение: Область определения: $x + 1 > 0 \Rightarrow x > -1$.
   Нули числителя: $x = 2$ (кратность 2), $x = -2$, $x = 4$.
   Метод интервалов на $(-1, +\infty)$:
   $-1 < x < 2$: $+$; $2 < x 4$: $+$.
   Включаем $x = 2$, $x = 4$.
   Ответ: $x \in (-1, 2] \cup [4, +\infty)$.
   
   
6. Если $x^{2}-8 x-3=(x+a)^{2}+b$, то чему равно значение $b$?
   Решение: Раскроем правую часть:
   $x^{2} + 2ax + a^{2} + b$. Сравнивая коэффициенты:
   $2a = -8 \Rightarrow a = -4$; $a^{2} + b = -3 \Rightarrow 16 + b = -3 \Rightarrow b = -19$.
   Ответ: $-19$.
   
   
7. $x_{1}$ и $x_{2}$ — корни уравнения $x^{2}-p x+10=0$. Решить уравнение, если $x_{1}^{2}+x_{2}^{2}=29$.
   Решение: По теореме Виета: $x_{1} + x_{2} = p$, $x_{1}x_{2} = 10$.
   $x_{1}^{2} + x_{2}^{2} = (x_{1} + x_{2})^{2} - 2x_{1}x_{2} = p^{2} - 20 = 29 \Rightarrow p^{2} = 49 \Rightarrow p = \pm7$.
   Уравнения: $x^{2} \pm7x + 10 = 0$. Корни:
   Для $p = 7$: $x = -2$, $x = -5$.
   Ответ: $-2$, $-5$.
   
   
8. Велосипедист проехал за 1,5 часа 36 км, а за следующие 2 часа еще 34 км. Найдите среднюю скорость велосипедиста.
   Решение: Общий путь: $36 + 34 = 70$ км. Время: $1,5 + 2 = 3,5$ ч.
   Средняя скорость: $\frac{70}{3,5} = 20$ км/ч.
   Ответ: 20.
   
   
9. Построить график $|y|=|x-1|$.
   Решение: График состоит из двух прямых:
   $y = |x - 1|$ и $y = -|x - 1|$, симметричных относительно оси $X$.
   Ответ: Объединение графиков $y = x - 1$ при $x \geq 1$, $y = 1 - x$ при $x < 1$ и их отражений относительно оси $X$.
   
   
10. Решить уравнение: $\left|x^{2}+4 x\right|=x^{2}-x-5$.
    Решение: Рассмотрим два случая:
    Случай 1: $x^{2} + 4x \geq 0 \Rightarrow x \leq -4$ или $x \geq 0$.
    Уравнение: $x^{2} + 4x = x^{2} - x - 5 \Rightarrow 5x = -5 \Rightarrow x = -1$ (не входит в область).
    Случай 2: $x^{2} + 4x < 0 \Rightarrow -4 < x < 0$.
    Уравнение: $-x^{2} - 4x = x^{2} - x - 5 \Rightarrow 2x^{2} + 3x - 5 = 0$.
    Дискриминант: $D = 9 + 40 = 49 \Rightarrow x = \frac{-3 \pm7}{4}$.
    Корни: $x = 1$ (не входит), $x = -2,5$.
    Ответ: $-2,5$.
    
    
11. Сравнить числа $a=3+2 \sqrt{5}$ и $b=\sqrt{14}+\sqrt{15}$.
    Решение: Возведем в квадрат:
    $a^{2} = 9 + 12\sqrt{5} + 20 = 29 + 12\sqrt{5}$.
    $b^{2} = 14 + 15 + 2\sqrt{210} = 29 + 2\sqrt{210}$.
    Сравним $12\sqrt{5}$ и $2\sqrt{210}$:
    $12\sqrt{5} = \sqrt{720}$, $2\sqrt{210} = \sqrt{840} \Rightarrow a < b$.
    Ответ: $a < b$.
    
    
12. При каких значениях $a$ уравнение $4 x^{3}+4 x^{2}+a x=0$ имеет два различных корня?
    Решение: Разложим: $x(4x^{2} + 4x + a) = 0$.
    Корни: $x = 0$ и корни квадратного уравнения. Для двух корней:
    Дискриминант квадратного уравнения: $D = 16 - 16a = 0 \Rightarrow a = 1$.
    Ответ: $a = 1$.
    
    
13. При каких значениях $a$ система $\left\{\begin{array}{l}y=x^{2}+4 x+3 \\ y=a\end{array}\right.$ имеет единственное решение?
    Решение: Парабола $y = x^{2} + 4x + 3$ имеет вершину в $x = -2$, $y = (-2)^{2} + 4(-2) + 3 = -1$.
    Ответ: $a = -1$.
    
    
14. Из Петербурга в Москву можно проехать двумя способами, а из Москвы в Хабаровск пятью способами. Сколькими способами можно проехать из Петербурга в Хабаровск?
    Решение: $2 \cdot 5 = 10$ способов.
    Ответ: 10.
    
    
15. Найдите координаты точки, через которую проходят все прямые вида $y+2=\kappa x+\kappa$.
    Решение: Преобразуем уравнение: $y = \kappa(x + 1) - 2$. При любом $\kappa$ прямая проходит через точку $(-1, -2)$.
    Ответ: $(-1, -2)$.
    
    
16. Диагонали ромба 16 см и 11 см. Найдите его площадь.
    Решение: Площадь ромба: $\frac{16 \cdot 11}{2} = 88$ см².
    Ответ: 88 см².
    
    
17. Около прямоугольного треугольника $ABC$ с прямым углом $C$ описана окружность. Найдите радиус этой окружности, если $BC=12$ см, $\angle A=30^{\circ}$.
    Решение: Гипотенуза $AB$ — диаметр окружности. В прямоугольном треугольнике с углом $30^{\circ}$: $BC = \frac{AB}{2} \Rightarrow AB = 24$ см. Радиус: $12$ см.
    Ответ: 12 см.
    
    
18. В прямоугольном треугольнике угол $C$ прямой, $\sin \angle A=\frac{2}{3}$. Найдите тангенс этого угла.
    Решение: $\cos A = \sqrt{1 - \left(\frac{2}{3}\right)^2} = \frac{\sqrt{5}}{3}$.
    $\tan A = \frac{\sin A}{\cos A} = \frac{2/3}{\sqrt{5}/3} = \frac{2}{\sqrt{5}} = \frac{2\sqrt{5}}{5}$.
    Ответ: $\frac{2\sqrt{5}}{5}$.
    
    
19. В равнобедренном треугольнике угол между высотами, проведёнными на боковые стороны, равен $80^{\circ}$. Найдите угол при вершине треугольника.
    Решение: Угол между высотами равен углу между боковыми сторонами. В равнобедренном треугольнике угол при вершине: $180^{\circ} - 80^{\circ} = 100^{\circ}$.
    Ответ: $100^{\circ}$.
    
    
20. В четырёхугольнике $ABCD$ точки $M, N, P, Q$ — середины сторон. Найдите площадь четырёхугольника $ABCD$, если площадь четырёхугольника $MNPQ$ равна $S$.
    Решение: Четырёхугольник $MNPQ$ — параллелограмм Вариньона, его площадь равна половине площади исходного четырёхугольника.
    Ответ: $2S$.