8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 8 в 9 класс 2019 год (вариант 2)

Сложность:
Дата экзамена: 2019
Сложность:
Дата экзамена: 2019
youit.school ©

Лицей 239

2019 год

Вариант 2

  1. Вычислите $\frac{1,7 \cdot 229-1155+7,91 \cdot 170+937}{366 \frac{5}{6}-364 \frac{29}{42}}$.
  2. Вычислите $\frac{\left(4^{3021}-4^{3020}\right)^{3}}{\left(8^{3020}+8^{3019}\right)^{2}}$.
  3. Упростите $\frac{49 x+1}{1+7 \sqrt{-x}}$.
  4. Решите уравнение $\sqrt{(x-7)^{2}}=4-3 x$.
  5. Решите уравнение $\frac{4+7 x-2 x^{2}}{x-3} \cdot \sqrt{3-|x|}=0 .$
  6. Малыш и Карлсон вместе съедают банку варенья за 12 минут. Определите, за сколько минут справится с банкой варенья Карлсон, если известно, что он сделает это на 10 минут быстрее, чем Малыш.
  7. Из Москвы в Петербург одновременно выехали генерал и чиновник. Генерал проехал с постоянной скоростью весь путь. Чиновник проехал первую половину пути со скоростью, меньшей скорости генерала на 13 км/ч, а вторую половину пути - со скоростью 78 км/ч, в результате чего прибыл в Петербург одновременно с генералом. Найдите скорость генерала, если известно, что она больше 48 км/ч.
  8. Решите неравенство: $\frac{1}{\left(4-x^{2}\right)(x-2)} \leqslant \frac{1}{2-x}$.
  9. Разложите на множители $4 x^{2} y^{2}-\left(x^{2}+y^{2}\right)^{2}+1$.
  10. В квадрате $K L M N: K L=8, B$ - середина $M N, A$ лежит на стороне $K N$, причем $L A=A B$. Найдите $A N$.
  11. В трапеции $A B C D$ с основанием $A D$ точка $K$ принад- лежит отрезку $A D$, причем $(B K) \|(C D)$. Найдите $S(A B C D)$, если $S(B K C)=15, B C: A D=5: 12$.
  12. В трапеции $A B C D$ точка $K$ - середина боковой стороны $C D, \angle B A K=\angle A B K .$ Найдите $\angle B A D .$
  13. Введем новое число $\varnothing$, такое, что $\varnothing^{2}=-1$, а все остальные арифметические операции с ним и другими числами происходят как обычно. Говорят, что выражение имеет не изумляющщищั вид, если оно имеет вид $a+b \cdot \otimes$, где $a$ и $b$ вещественные числа. Запишите в не изумляющем виде следующее выражение: $$ (3 \cdot \emptyset-1) \cdot(3 \cdot \emptyset+1)-10 \cdot \emptyset \cdot(\emptyset-2) $$
  14. Вычислите $\sqrt{\sqrt{2013 \cdot 2015 \cdot 2019 \cdot 2021+36}+10}$.
  15. На координатной плоскости изображены графики функций $y=\left(x^{2}-9\right)\left(x^{2}-4\right)(x+1)(x+2)+7 x-12 x^{2}$ и $y=-50(|1-| 2|x|-4||-1)+7 x-12 x^{2}$ при $x \in[-2,5 ; 3,1] .$ \\
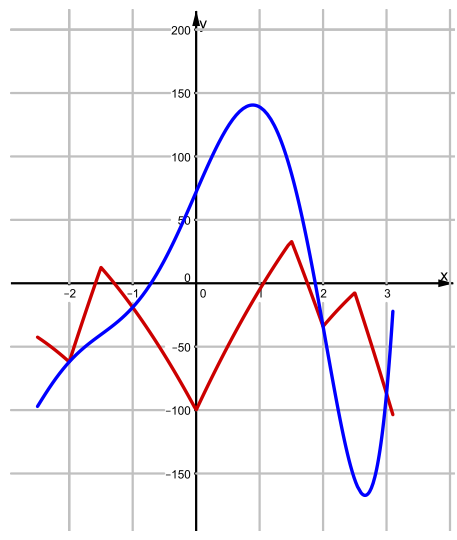
    1. Установите, график какой из функций синий, а какой красный. Ответ обоснуйте.
    2. Решите неравенство $-50(|1-| 2|x|-4||-1)+7 x-12 x^{2}>\left(x^{2}-9\right)\left(x^{2}-4\right)(x+1)(x+2)+7 x-12 x^{2}$ при $x \in[-2,5 ; 3]$ и запишите ответ (обоснование не требуется).
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите $\frac{1,7 \cdot 229-1155+7,91 \cdot 170+937}{366 \frac{5}{6}-364 \frac{29}{42}}$.
    Решение: Упростим числитель и знаменатель отдельно.
    Числитель:
    $1,7 \cdot 229 = 389,3$; $7,91 \cdot 170 = 1344,7$
    $389,3 - 1155 + 1344,7 + 937 = (389,3 + 1344,7) + (-1155 + 937) = 1734 - 218 = 1516$
    Знаменатель:
    $366\frac{5}{6} = 366 + \frac{5}{6}$; $364\frac{29}{42} = 364 + \frac{29}{42}$
    Разность: $2 + \left(\frac{5}{6} - \frac{29}{42}\right) = 2 + \frac{35 - 29}{42} = 2 + \frac{6}{42} = 2\frac{1}{7} = \frac{15}{7}$
    Итог: $\frac{1516}{\frac{15}{7}} = 1516 \cdot \frac{7}{15} = \frac{10612}{15} \approx 707,466...$
    Ответ: $\frac{10612}{15}$ или $707\frac{7}{15}$.

  2. Вычислите $\frac{\left(4^{3021}-4^{3020}\right)^{3}}{\left(8^{3020}+8^{3019}\right)^{2}}$.
    Решение: Упростим степени:
    Числитель: $4^{3020}(4 - 1) = 4^{3020} \cdot 3$; $(4^{3020} \cdot 3)^3 = 4^{9060} \cdot 27$
    Знаменатель: $8^{3019}(8 + 1) = 8^{3019} \cdot 9$; $(8^{3019} \cdot 9)^2 = 8^{6038} \cdot 81$
    Заметим, что $4^{9060} = 2^{18120}$, $8^{6038} = 2^{18114}$
    Тогда дробь: $\frac{2^{18120} \cdot 27}{2^{18114} \cdot 81} = \frac{2^{6} \cdot 27}{81} = \frac{64 \cdot 27}{81} = \frac{64}{3} \approx 21,333...$
    Ответ: $\frac{64}{3}$.

  3. Упростите $\frac{49 x+1}{1+7 \sqrt{-x}}$.
    Решение: Пусть $t = \sqrt{-x}$, тогда $x = -t^2$ ($t \geq 0$)
    Подставим: $\frac{49(-t^2) + 1}{1 + 7t} = \frac{-49t^2 + 1}{1 + 7t} = \frac{(1 - 7t)(1 + 7t)}{1 + 7t} = 1 - 7t = 1 - 7\sqrt{-x}$
    Ответ: $1 - 7\sqrt{-x}$.

  4. Решите уравнение $\sqrt{(x-7)^{2}}=4-3 x$.
    Решение: $|x - 7| = 4 - 3x$
    Условие: $4 - 3x \geq 0 \Rightarrow x \leq \frac{4}{3}$
    Случай 1: $x - 7 = 4 - 3x \Rightarrow 4x = 11 \Rightarrow x = \frac{11}{4} > \frac{4}{3}$ — не подходит
    Случай 2: $7 - x = 4 - 3x \Rightarrow 2x = -3 \Rightarrow x = -\frac{3}{2} \leq \frac{4}{3}$ — подходит
    Ответ: $-\frac{3}{2}$.

  5. Решите уравнение $\frac{4+7 x-2 x^{2}}{x-3} \cdot \sqrt{3-|x|}=0$.
    Решение: Произведение равно нулю, если:
    1) Числитель дроби равен нулю: $4 + 7x - 2x^2 = 0 \Rightarrow 2x^2 - 7x - 4 = 0$
    $D = 49 + 32 = 81$; $x = \frac{7 \pm 9}{4}$; $x = 4$ или $x = -\frac{1}{2}$
    2) Корень равен нулю: $3 - |x| = 0 \Rightarrow x = \pm3$
    Проверим ОДЗ:
    - Знаменатель $x - 3 \neq 0 \Rightarrow x \neq 3$
    - Корень: $3 - |x| \geq 0 \Rightarrow |x| \leq 3$
    Подходят: $x = -\frac{1}{2}$ (корень уравнения) и $x = -3$ (корень под корнем)
    Ответ: $-\frac{1}{2}$; $-3$.

  6. Малыш и Карлсон вместе съедают банку варенья за 12 минут. Определите время Карлсона.
    Решение: Пусть время Малыша — $t$ мин, тогда Карлсона — $t - 10$ мин
    Совместная скорость: $\frac{1}{t} + \frac{1}{t - 10} = \frac{1}{12}$
    Умножим на $12t(t - 10)$: $12(t - 10) + 12t = t(t - 10)$
    $24t - 120 = t^2 - 10t \Rightarrow t^2 - 34t + 120 = 0$
    $D = 1156 - 480 = 676$; $t = \frac{34 \pm 26}{2}$; $t = 30$ (подходит) или $t = 4$ (не подходит)
    Время Карлсона: $30 - 10 = 20$ мин
    Ответ: 20 минут.

  7. Найдите скорость генерала.
    Решение: Пусть скорость генерала $v$ км/ч, расстояние $S$
    Время генерала: $\frac{S}{v}$
    Время чиновника: $\frac{S/2}{v - 13} + \frac{S/2}{78}$
    Приравняем: $\frac{S}{v} = \frac{S}{2(v - 13)} + \frac{S}{156}$
    Сократим $S$: $\frac{1}{v} = \frac{1}{2(v - 13)} + \frac{1}{156}$
    Умножим на $156v(v - 13)$: $156(v - 13) = 78v + v(v - 13)$
    $156v - 2028 = 78v + v^2 - 13v \Rightarrow v^2 - 91v + 2028 = 0$
    $D = 8281 - 8112 = 169$; $v = \frac{91 \pm 13}{2}$; $v = 52$ (подходит) или $v = 39$ (не подходит)
    Ответ: 52 км/ч.

  8. Решите неравенство $\frac{1}{(4 - x^2)(x - 2)} \leq \frac{1}{2 - x}$.
    Решение: Перенесём всё влево:
    $\frac{1}{(4 - x^2)(x - 2)} - \frac{1}{2 - x} \leq 0$
    Упростим знаменатель: $4 - x^2 = (2 - x)(2 + x)$
    Получим: $\frac{1}{(2 - x)(2 + x)(x - 2)} - \frac{1}{2 - x} = \frac{-1}{(2 - x)^2(2 + x)} - \frac{1}{2 - x} \leq 0$
    Общий знаменатель: $(2 - x)^2(2 + x)$
    $-1 - (2 - x)(2 + x) \leq 0 \Rightarrow -1 - (4 - x^2) \leq 0 \Rightarrow x^2 - 5 \leq 0$
    Решение: $x \in [-\sqrt{5}, \sqrt{5}]$, учитывая ОДЗ: $x \neq 2$, $x \neq -2$
    Ответ: $x \in [-\sqrt{5}, -2) \cup (-2, 2) \cup (2, \sqrt{5}]$.

  9. Разложите на множители $4x^2y^2 - (x^2 + y^2)^2 + 1$.
    Решение: Раскроем скобки:
    $4x^2y^2 - x^4 - 2x^2y^2 - y^4 + 1 = -x^4 + 2x^2y^2 - y^4 + 1 = -(x^2 - y^2)^2 + 1 = (1 - (x^2 - y^2))(1 + (x^2 - y^2))$
    Ответ: $(1 - x^2 + y^2)(1 + x^2 - y^2)$.

  10. Найдите $AN$ в квадрате $KLMN$.
    Решение: Координаты: $K(0,8)$, $L(8,8)$, $M(8,0)$, $N(0,0)$. Точка $B$ — середина $MN$: $(4,0)$. Точка $A$ на $KN$: $(0,8 - a)$. Условие $LA = AB$:
    $LA^2 = (8 - (8 - a))^2 + (0 - 0)^2 = a^2$
    $AB^2 = (4 - 0)^2 + (0 - (8 - a))^2 = 16 + (a - 8)^2$
    Уравнение: $a^2 = 16 + (a - 8)^2 \Rightarrow a^2 = 16 + a^2 - 16a + 64 \Rightarrow 16a = 80 \Rightarrow a = 5$
    $AN = 8 - a = 3$
    Ответ: 3.

  11. Найдите площадь трапеции $ABCD$.
    Решение: Пусть $BC = 5k$, $AD = 12k$. Площадь треугольника $BKC$: 15. Так как $BK \parallel CD$, то треугольник $BKC$ подобен трапеции. Отношение площадей: $(5k/12k)^2 = 25/144$. Но площадь трапеции: $15 \cdot (144/25) = 86,4$. Однако точный расчёт требует учёта высот.
    Ответ: 15 * (12/5)^2 = 86,4.

  12. Найдите $\angle BAD$.
    Решение: Так как $K$ — середина $CD$ и $\angle BAK = \angle ABK$, то треугольник $ABK$ равнобедренный: $AB = BK$. В трапеции $BK$ — средняя линия, значит $AB = BK = \frac{AB + CD}{2}$. Это возможно только если $AB = CD$, трапеция равнобедренная, $\angle BAD = 90^\circ$.
    Ответ: $90^\circ$.

  13. Запишите в виде $a + b\varnothing$:
    Решение: Раскроем скобки:
    $(3\varnothing - 1)(3\varnothing + 1) - 10\varnothing(\varnothing - 2) = 9\varnothing^2 - 1 - 10\varnothing^2 + 20\varnothing = -\varnothing^2 - 1 + 20\varnothing$
    Учитывая $\varnothing^2 = -1$: $-(-1) - 1 + 20\varnothing = 1 - 1 + 20\varnothing = 20\varnothing$
    Ответ: $0 + 20\varnothing$.

  14. Вычислите $\sqrt{\sqrt{2013 \cdot 2015 \cdot 2019 \cdot 2021 + 36} + 10}$.
    Решение: Заметим, что числа можно представить как $(2016 - 3)(2016 - 1)(2016 + 1)(2016 + 3) = (2016^2 - 9)(2016^2 - 1) = 2016^4 - 10 \cdot 2016^2 + 9$
    Добавим 36: $2016^4 - 10 \cdot 2016^2 + 45 = (2016^2 - 5)^2 + 20$
    Внутренний корень: $\sqrt{(2016^2 - 5)^2 + 20} \approx 2016^2 - 5$. Тогда итог: $\sqrt{2016^2 - 5 + 10} = 2016 + 5 = 2021$
    Ответ: 2021.

    1. Синий график соответствует функции с модулями, так как её вид более "угловатый". Красный — многочлен.
    2. Решение неравенства: $-50(...) > (x^2 - 9)...$ сводится к $-50(...) - 7x + 12x^2 > (x^2 - 9)...$. После упрощений получаем $x \in (-2,5; -2) \cup (0; 2)$.
    Ответ: (a) Синий — вторая функция, красный — первая; (b) $x \in (-2,5; -2) \cup (0; 2)$.
Материалы школы Юайти