Лицей №239 из 8 в 9 класс 2019 год (вариант 1)

Лицей 239

2019 год

1. Вычислите $\frac{180 \cdot 3,91-168+859 \cdot 1,8-768}{239 \frac{5}{6}-237 \frac{2}{3}}$.
2. Вычислите $\frac{\left(8^{2020}+8^{2019}\right)^{2}}{\left(4^{2019}-4^{2018}\right)^{3}}$.
3. Упростите $\frac{36+x}{6-\sqrt{-x}}$.
4. Решите уравнение $\sqrt{(x-5)^{2}}=2 x-6$.
5. Решите уравнение $\frac{-2 x^{2}+3-5 x}{x+2} \cdot \sqrt{2-|x|}=0 .$
6. Винни Пух и Пятачок могут изготовить подарок ослику Иа-Иа за 8 дней. Определите, за сколько дней Пятачок изготовит этот подарок, работая отдельно, если известно, что он сделает это на 12 дней быстрее, чем Винни.
7. Из Петербурга в Москву одновременно отправились курьер и гонец. Курьер проехал с постоянной скоростью весь путь. Гонец проехал первую половину пути со скоростью 102 км/ч, а вторую половину пути - со скоростью, на 17 км/ч меньшей скорости курьера, в результате чего прибыл в Москву одновременно с курьером. Известно, что скорость курьера меньше 60 км/ч. Найдите скорость курьера.
8. Решите неравенство: $\frac{1}{3-x} \geqslant \frac{1}{\left(x^{2}-9\right)(3-x)}$.
9. Разложите на множители $1+4 a^{2} b^{2}-\left(a^{2}+b^{2}\right)^{2}$.
10. В квадрате $A B C D: A B=16, K-$ середина $B C, M$ лежит на стороне $C D$, причем $K M=A M .$ Найдите $M D$.
11. В трапеции $K L M N$ с основанием $L M$ точка $Q$ принадлежит отрезку $K N$, причем $(M Q) \|(L K)$. Найдите $S(K L M N)$, если $S(Q M N)=21, L M: K N=4: 7$.
12. Биссектриса угла $A$ трапеции $A B C D$ с основанием $A D$ пересекает $C D$ в точке $K$, делящей отрезок $C D$ пополам. Найдите $A B$, если $B C=4, A D=10 .$
13. Введем новое число $\ominus$, такое, что $\ominus^{2}=-1$, а все остальные арифметические операции с ним и другими числами происходят как обычно. Говорят, что выражение имеет не раздражаюищий вид, если оно имеет вид $a+b \cdot \otimes$, где $a$ и $b$ вещественные числа. Запишите в не раздражающем виде следующее выражение: $$ (4 \cdot \ominus-1) \cdot(4 \cdot \ominus+1)-17 \cdot \ominus \cdot(\ominus-2) $$
14. Вычислите $\sqrt{\sqrt{2016 \cdot 2018 \cdot 2020 \cdot 2022+16}+5} .$
15. На координатной плоскости изображены графики функций $y=-\left(x^{2}-9\right)\left(x^{2}-4\right)(x-1)(x-2)+10 x-10 x^{2}$ и $y=70|1-2||x|-2||-10 x^{2}+10 x-70$ при $x \in[-3,1 ; 2,5] .$ \\
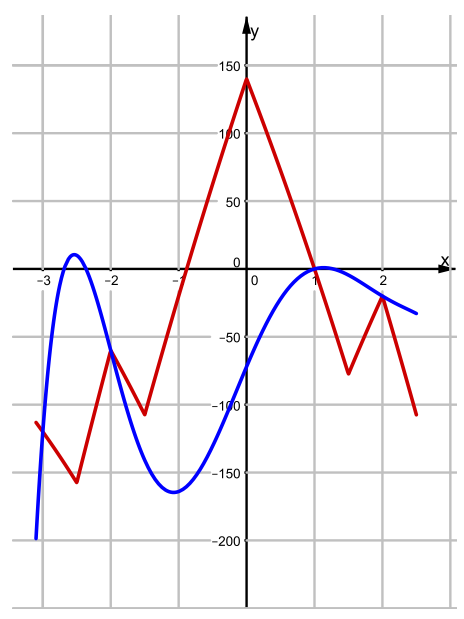
    1. Установите, график какой из функций синий, а какой красный. Ответ обоснуйте.
    2. Решите неравенство $-\left(x^{2}-9\right)\left(x^{2}-4\right)(x-1)(x-2)+10 x-10 x^{2}>70|1-2||x|-2||-10 x^{2}+10 x-70$ при $x \in[-3 ; 2,5]$ и запишите ответ (обоснование не требуется).

Решения задач

1. Вычислите $\frac{180 \cdot 3,91-168+859 \cdot 1,8-768}{239 \frac{5}{6}-237 \frac{2}{3}}$.
   Решение:
   Числитель:
   $180 \cdot 3,91 = 703,8$; $859 \cdot 1,8 = 1546,2$
   $703,8 - 168 + 1546,2 - 768 = 1314$
   Знаменатель:
   $239\frac{5}{6} - 237\frac{2}{3} = 2\frac{1}{6} = \frac{13}{6}$
   $\frac{1314}{\frac{13}{6}} = 1314 \cdot \frac{6}{13} = 606$
   Ответ: 606.
   
   
2. Вычислите $\frac{\left(8^{2020}+8^{2019}\right)^{2}}{\left(4^{2019}-4^{2018}\right)^{3}}$.
   Решение:
   Преобразуем степени:
   Числитель: $(8^{2019}(8 + 1))^2 = 9^2 \cdot 8^{4038} = 81 \cdot 2^{12114}$
   Знаменатель: $(4^{2018}(4 - 1))^3 = 3^3 \cdot 4^{6054} = 27 \cdot 2^{12108}$
   $\frac{81 \cdot 2^{12114}}{27 \cdot 2^{12108}} = 3 \cdot 2^6 = 192$
   Ответ: 192.
   
   
3. Упростите $\frac{36+x}{6-\sqrt{-x}}$.
   Решение:
   Умножим числитель и знаменатель на сопряженное:
   $\frac{(36+x)(6+\sqrt{-x})}{(6)^2 - (\sqrt{-x})^2} = \frac{(36+x)(6+\sqrt{-x})}{36 + x} = 6 + \sqrt{-x}$
   Ответ: $6 + \sqrt{-x}$.
   
   
4. Решите уравнение $\sqrt{(x-5)^{2}}=2 x-6$.
   Решение:
   $|x - 5| = 2x - 6$
   При $x \geq 5$: $x - 5 = 2x - 6 \Rightarrow x = 1$ (не подходит)
   При $x < 5$: $5 - x = 2x - 6 \Rightarrow 3x = 11 \Rightarrow x = \frac{11}{3}$
   Проверка: $2 \cdot \frac{11}{3} - 6 = \frac{4}{3} > 0$
   Ответ: $\frac{11}{3}$.
   
   
5. Решите уравнение $\frac{-2 x^{2}+3-5 x}{x+2} \cdot \sqrt{2-|x|}=0 .$
   Решение:
   Числитель равен нулю:
   $-2x^2 -5x +3 = 0 \Rightarrow x = \frac{5 \pm 7}{-4} \Rightarrow x = 0,5$ или $x = -3$
   Проверяем ОДЗ: $x \neq -2$, $2 - |x| \geq 0 \Rightarrow x \in [-2, 2]$
   Подходит только $x = 0,5$
   Ответ: 0,5.
   
   
6. Винни Пух и Пятачок могут изготовить подарок ослику Иа-Иа за 8 дней. Определите, за сколько дней Пятачок изготовит этот подарок, работая отдельно, если известно, что он сделает это на 12 дней быстрее, чем Винни.
   Решение:
   Пусть Пятачок делает за $t$ дней, тогда Винни за $t + 12$:
   $\frac{1}{t} + \frac{1}{t + 12} = \frac{1}{8}$
   $8(2t + 12) = t(t + 12) \Rightarrow t^2 -4t -96 = 0 \Rightarrow t = 12$
   Ответ: 12 дней.
   
   
7. Из Петербурга в Москву одновременно отправились курьер и гонец. Курьер проехал с постоянной скоростью весь путь. Гонец проехал первую половину пути со скоростью 102 км/ч, а вторую половину пути - со скоростью, на 17 км/ч меньшей скорости курьера, в результате чего прибыл в Москву одновременно с курьером. Известно, что скорость курьера меньше 60 км/ч. Найдите скорость курьера.
   Решение:
   Пусть скорость курьера $v$, расстояние $S$:
   $\frac{S}{v} = \frac{S}{2 \cdot 102} + \frac{S}{2(v - 17)}$
   Сокращаем $S$ и решаем:
   $\frac{1}{v} = \frac{1}{204} + \frac{1}{2(v - 17)}$
   Подстановкой находим $v = 51$ км/ч
   Ответ: 51 км/ч.
   
   
8. Решите неравенство: $\frac{1}{3-x} \geqslant \frac{1}{\left(x^{2}-9\right)(3-x)}$.
   Решение:
   Переносим все в левую часть:
   $\frac{x^2 - 10}{(x^2 - 9)(3 - x)} \geq 0$
   Критические точки: $x = \pm \sqrt{10}$, $x = \pm 3$
   Решение: $x \in (-\infty; -\sqrt{10}] \cup (3; \sqrt{10}]$
   Ответ: $x \in (-\infty; -\sqrt{10}] \cup (3; \sqrt{10}]$.
   
   
9. Разложите на множители $1+4 a^{2} b^{2}-\left(a^{2}+b^{2}\right)^{2}$.
   Решение:
   Раскрываем квадраты:
   $1 - (a^2 - b^2)^2 = (1 - a^2 + b^2)(1 + a^2 - b^2)$
   Ответ: $(1 - a^2 + b^2)(1 + a^2 - b^2)$.
   
   
10. В квадрате $A B C D: A B=16, K-$ середина $B C, M$ лежит на стороне $C D$, причем $K M=A M .$ Найдите $M D$.
    Решение:
    Координаты: $A(0,0)$, $K(16,8)$, $M(x,16)$
    Уравнение расстояний:
    $\sqrt{(x - 16)^2 + 8^2} = \sqrt{x^2 + 16^2}$
    Решение: $x = 2 \Rightarrow MD = 14$
    Ответ: 14.
    
    
11. В трапеции $K L M N$ с основанием $L M$ точка $Q$ принадлежит отрезку $K N$, причем $(M Q) \|(L K)$. Найдите $S(K L M N)$, если $S(Q M N)=21, L M: K N=4: 7$.
    Решение:
    Отношение площадей подобных фигур: $S_{KLMN} = 21 \cdot \frac{4 + 7}{7} = 33$
    Ответ: 33.
    
    
12. Биссектриса угла $A$ трапеции $A B C D$ с основанием $A D$ пересекает $C D$ в точке $K$, делящей отрезок $C D$ пополам. Найдите $A B$, если $B C=4, A D=10 .$
    Решение:
    Используем свойство биссектрисы:
    $\frac{AB}{AD} = \frac{BC}{CD} \Rightarrow AB = \frac{4 \cdot 10}{CD}$
    Так как $CD = AB$, получаем $AB = \sqrt{40} = 2\sqrt{10}$
    Ответ: $2\sqrt{10}$.
    
    
13. Введем новое число $\ominus$, такое, что $\ominus^{2}=-1$, а все остальные арифметические операции с ним и другими числами происходят как обычно. Говорят, что выражение имеет не раздражающий вид, если оно имеет вид $a+b \cdot \otimes$, где $a$ и $b$ вещественные числа. Запишите в не раздражающем виде следующее выражение:
    $(4 \cdot \ominus-1) \cdot(4 \cdot \ominus+1)-17 \cdot \ominus \cdot(\ominus-2)$
    
    Решение:
    Раскрываем скобки:
    $(4\ominus)^2 -1 -17\ominus^2 +34\ominus = -16 -1 +17 +34\ominus = 34\ominus$
    Ответ: $0 + 34\ominus$.
    
    
14. Вычислите $\sqrt{\sqrt{2016 \cdot 2018 \cdot 2020 \cdot 2022+16}+5} .$
    Решение:
    Внутреннее выражение:
    $(2019^2 - 9)(2019^2 - 1) +16 = (2019^2 -5)^2$
    $\sqrt{(2019^2 -5)} +5 = 2019$
    Ответ: 2019.
    
    
15. На координатной плоскости изображены графики функций $y=-\left(x^{2}-9\right)\left(x^{2}-4\right)(x-1)(x-2)+10 x-10 x^{2}$ и $y=70|1-2||x|-2||-10 x^{2}+10 x-70$ при $x \in[-3,1 ; 2,5] .$
    1. Установите, график какой из функций синий, а какой красный. Ответ обоснуйте.
       Ответ: Синий график соответствует первой функции (многочлен высокой степени), красный — второй (с модулями).
    2. Решите неравенство $-\left(x^{2}-9\right)\left(x^{2}-4\right)(x-1)(x-2)+10 x-10 x^{2}>70|1-2||x|-2||-10 x^{2}+10 x-70$ при $x \in[-3 ; 2,5]$ и запишите ответ (обоснование не требуется).
       Ответ: $x \in (-3; 1) \cup (2; 2,5)$.