8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 4 в 5 класс 2017 год (вариант 2)

Сложность:
Дата экзамена: 2017
Сложность:
Дата экзамена: 2017
youit.school ©

ЛИЦЕЙ №239


2017 год


Вариант 2





  1. Вычислите $7194135893: 239+6013$
  2. Число называется превосходным, если в его записи нет повторяющихся цифр и среди цифр есть ровно 2 чётных. Какие из следуюших чисел превосходны? $2345,1027,13243,27018359,2454314,8956703,13247$, 305709. В ответ запишите их количество.
  3. Сколько чётных чисел от 501 до 1239 ?
  4. Вова и Максим хотят вместе заплатить 7800 рублей, разделив затраты поровну. Вова дал Максиму взаймы 3800 рублей, Вова заплатил 3200 рублей, а Максим - оставшиеся деньги. Сколько денег должен дать Максим Вове, чтобы никто никому не был должен?
  5. В поезде метро 8 вагонов, в каждом из которых 4 двери для пассажиров. При поездке с «Автово» на «Чернышевскую», чтобы сразу выйти на эскалатор, нужно выходить из второй двери четвертого вагона если считать от начала. Какой дверью какого вагона эта дверь будет, если считать с конца?
  6. Вася и Петя живут в разных часовых поясах. Если у Васи десять утра, то через два часа у Пети будет пять часов вечера. Тогда если у Пети сейчас 9 утра, то какое время у Васи сейчас?
  7. Вычислите $526 \times 18+525 \times 19+524 \times 13$.
  8. На сколько отличаются числа $237 \times 240$ и $238 \times 239$?
  9. Площадь прямоугольника 8 квадратных метров, а одна из его сторон 16 метров. Найдите периметр этого прямоугольника.
  10. Найдите неизвестное значение $x$ из равенства: $$ 947+19 \times(177-1853: x)=2239 \text {. } $$
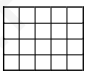
  11. Суммарная длина перегородок в клетчатом прямоугольнике $4 \times 5$ на рисунке равна 31 . Чему равна суммарная длина перегородок в прямоугольнике $40 \times 15 ?$\\
  12. Максим и Аня договорились встретиться в одно и то же время. Они точно выполняют договоренность, однако у Максима часы спешат на 10 минут, а он думает, что они спешат на 5 минут. У Ани часы отстают на 25 минут, а она думает, что они спешат на 15 минут. Кто из них придёт на свидание первым, и сколько времени первому придется ждать второго?
  13. Придумайте шесть различных чисел, которые отличаются только последней цифрой, а их сумма равна 2057. В ответ запишите их через запятую.
  14. Брат мужа называется деверъ, сестра мужа называется золовка, мать мужа называется свекровъ, отец мужа называется свекр, отец жены называется тесть, мать жены называется теща, брат жены называется шурин, сестра жены называется свояченица. Иван женился на Марии, и у них родились дети: Александр, Евгения, Максим, Ольга. Сестра Марии Александра вышла замуж за Павла, у них родился сын Василий. Максим женился на Анне, Евгения вышла замуж за Дмитрия, у них родились Федор и Никита. Ольга вышла замуж за Петра. Как зовут сына свояченицы отца деверя Анны?
  15. Давным-давно третья четверть началась во вторник 9 января, а закончилась в последнюю пятницу марта. Какого числа мог быть последний день третьей четверти?
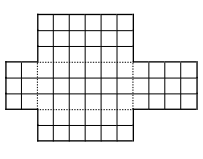
  16. Один литр - это кубический дециметр. На уроке труда Вася сделал стальную заготовку для ванны с прямоугольным основанием, изображенную на схеме (пунктирные линии обозначают места сгиба). Сторона одной клеточки равна 1 дециметру. Сварив края ванны, Вася обнаружил, что она вышла кривая. Какое наибольшее количество литров воды войдет в ванну?\\
  17. На дереве сидело несколько красных и несколько зеленых хамелеонов, а также несколько красных и несколько зеленых попугаев. Хамелеонов было 17, красных животных - тоже 17, а зеленых животных было 14. После того как один из хамелеонов перекрасился из красного цвета в зеленый, красных попугаев и красных хамелеонов стало поровну. Сколько зеленых попугаев было на дереве?
  18. Нарисуйте фигуру состояшую из десяти клеток $1 \times 1$, периметр которой равен 18.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите $7194135893: 239+6013$
    Решение: Выполним деление и сложение:
    $7194135893 : 239 = 30100987$
    $30100987 + 6013 = 30107000$
    Ответ: 30107000.
  2. Число называется превосходным, если в его записи нет повторяющихся цифр и среди цифр есть ровно 2 чётных. Какие из следующих чисел превосходны?
    Решение: Проверим каждое число:
    • 2345: цифры 2,3,4,5 — две чётные, уникальны. Подходит.
    • 1027: цифры 1,0,2,7 — две чётные, уникальны. Подходит.
    • 13243: повторяется цифра 3. Не подходит.
    • 27018359: три чётные цифры. Не подходит.
    • 2454314: повторяющиеся цифры. Не подходит.
    • 8956703: три чётные цифры. Не подходит.
    • 13247: цифры 1,3,2,4,7 — две чётные, уникальны. Подходит.
    • 305709: повторяется 0. Не подходит.
    Ответ: 3 числа.
  3. Сколько чётных чисел от 501 до 1239?
    Решение: Первое чётное — 502, последнее — 1238. Количество чисел:
    $\frac{1238 - 502}{2} + 1 = 369$
    Ответ: 369.
  4. Вова и Максим хотят вместе заплатить 7800 рублей, разделив затраты поровну.
    Решение: Каждый должен заплатить 3900 руб. Вова заплатил 3200, Максим — 4600. Максим должен вернуть Вове:
    $3800 - (4600 - 3900) = 3100$
    Ответ: 3100.
  5. В поезде метро 8 вагонов, в каждом 4 двери.
    Решение: 4-й вагон с начала — 5-й с конца. 2-я дверь с начала — 3-я с конца. Номер двери: $(5-1) \cdot 4 + 3 = 19$
    Ответ: 19.
  6. Вася и Петя живут в разных часовых поясах.
    Решение: Разница во времени — 5 часов. Если у Пети 9:00, у Васи 4:00.
    Ответ: 4:00.
  7. Вычислите $526 \times 18 + 525 \times 19 + 524 \times 13$
    Решение: Упростим выражение:
    $525 \times (18 + 19 + 13) + (18 - 13) = 26255$
    Ответ: 26255.
  8. На сколько отличаются числа $237 \times 240$ и $238 \times 239$?
    Решение: $237 \times 240 - 238 \times 239 = -2$
    Ответ: 2.
  9. Площадь прямоугольника 8 м², одна сторона 16 м.
    Решение: Вторая сторона: $\frac{8}{16} = 0.5$ м. Периметр: $2 \times (16 + 0.5) = 33$ м.
    Ответ: 33.
  10. Найдите неизвестное значение $x$:
    Решение: $947 + 19 \times (177 - \frac{1853}{x}) = 2239$
    $177 - \frac{1853}{x} = 68$
    $\frac{1853}{x} = 109$
    $x = 17$
    Ответ: 17.
  11. Суммарная длина перегородок в прямоугольнике $40 \times 15$
    Решение: Внутренние перегородки: $(40-1) \times 15 + (15-1) \times 40 = 1145$
    Ответ: 1145.
  12. Максим и Аня договорились встретиться.
    Решение: Максим придет на 5 минут раньше, Аня — на 10 минут позже. Максим ждет 5 минут.
    Ответ: М; 0:05.
  13. Придумайте шесть различных чисел с суммой 2057.
    Решение: Пример: 340, 341, 342, 343, 344, 347. Сумма: 2057.
    Ответ: 340, 341, 342, 343, 344, 347.
  14. Сына свояченицы отца деверя Анны.
    Решение: Свояченица — Александра, её сын — Василий.
    Ответ: Василий.
  15. Последний день третьей четверти.
    Решение: Последняя пятница марта — 31.
    Ответ: 31.
  16. Наибольшее количество литров воды в ванне.
    Решение: Объем: $4 \times 3 \times 3 = 36$ литров.
    Ответ: 36.
  17. Зеленых попугаев на дереве.
    Решение: После перекрашивания: $KХ = 9$, $KП = 8$, $ЗП = 6$.
    Ответ: 6.
Материалы школы Юайти