Лицей №239 из 4 в 5 класс 2012 год (вариант 2)

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239

2012 год

Вариант 2

В задачах, отмеченных *, требуется записать решение, а не только ответ!

1. Сколько натуральных чисел от 30 до 330 делится на 3?
2. Какова сумма наибольшего и наименьшего четырехзначных чисел, все цифры которых различны?
3. В летнем лагере 218 детей и 26 воспитателей. В автобус помещается не более 45 пассажиров. Сколько автобусов потребуется, чтобы перевезти всех из лагеря в город?
4. *В пиратской шайке 50 человек. Из них 32 одноруких, 29 одноглазых, 15 – одноруких с одним глазом. Сколько здоровых пиратов в шайке?
5. В лесу проводился кросс. Белка сказала: «Первое место занял заяц, а второй была лиса». Другая белка возразила: «Заяц занял второе место, а лось был первым». На что филин заметил, что в высказывании каждой белки одна часть верная, а другая нет. Кто был первым, а кто вторым в кроссе?
6. *Вычислите: (60501: $67-68595: 85) \cdot 643$
7. *Решите уравнение: $20:(33-4 \cdot x)+47=51$
8. Расставьте между числами знаки действий и скобки так, чтобы получилось верное равенство:
   6 8 20 4 2 =58
9. Расставьте в клетках данной таблицы числа 0, 1, 2, 3, 4, 5, 6, 7, 8 (по одному каждое) так, чтобы сумма чисел в каждой строке, каждом столбце и на двух главных диагоналях была одинаковой.
   
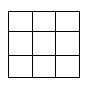
10. *Найдите периметр и площадь прямоугольника, у которого длина 18 см, и она больше ширины на 5 см.
11. *Муха летит со скоростью 5 м/с. Сколько километров она пролетит за час?
12. *Шапокляк и Крокодил Гена едут по одной дороге в одном направлении. Сейчас между ними 105 км. Какова скорость Крокодила, если Шапокляк, скорость которой 90 км/ч, догнала его через 3 часа?
13. Марина ходит в спортзал один раз в 6 дней, Маша – один раз в 3 дня, а Катя – один раз в 4 дня. Они встретились в спортзале в субботу. В какой день недели они встретятся вновь?
14. *На какую цифру оканчивается разность $4 \cdot 14 \cdot 24 \cdot \ldots \cdot 20124-1 ?$
15. *Сколько различных трехзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая из этих цифр может быть использована только один раз?

Решения задач

1. Сколько натуральных чисел от 30 до 330 делится на 3?
   Решение: Первое число в диапазоне, делящееся на 3: 30, последнее: 330. Количество чисел: $\frac{330 - 30}{3} + 1 = 101$.
   Ответ: 101.
2. Какова сумма наибольшего и наименьшего четырехзначных чисел, все цифры которых различны?
   Решение: Наибольшее: 9876, наименьшее: 1023. Сумма: $9876 + 1023 = 10899$.
   Ответ: 10899.
3. В летнем лагере 218 детей и 26 воспитателей. В автобус помещается не более 45 пассажиров. Сколько автобусов потребуется, чтобы перевезти всех из лагеря в город?
   Решение: Всего пассажиров: $218 + 26 = 244$. Количество автобусов: $\lceil \frac{244}{45} \rceil = 6$.
   Ответ: 6 автобусов.
4. *В пиратской шайке 50 человек. Из них 32 одноруких, 29 одноглазых, 15 – одноруких с одним глазом. Сколько здоровых пиратов в шайке?
   Решение: По формуле включений-исключений:
   Здоровые = Всего - (Однорукие + Одноглазые - Однорукие и одноглазые)
   $50 - (32 + 29 - 15) = 50 - 46 = 4$.
   Ответ: 4 пирата.
5. В лесу проводился кросс. Белка сказала: «Первое место занял заяц, а второй была лиса». Другая белка возразила: «Заяц занял второе место, а лось был первым». На что филин заметил, что в высказывании каждой белки одна часть верная, а другая нет. Кто был первым, а кто вторым в кроссе?
   Решение: Если первая часть первой белки верна (заяц первый), то вторая часть второй белки (лось первый) ложна. Тогда вторая часть первой белки (лиса вторая) должна быть ложной, что противоречит условию. Следовательно, верно: лось первый, лиса вторая.
   Ответ: лось первый, лиса вторая.
6. *Вычислите: $(60501: 67-68595: 85) \cdot 643$
   Решение:
   $60501 : 67 = 903$; $68595 : 85 = 807$;
   $(903 - 807) \cdot 643 = 96 \cdot 643 = 61728$.
   Ответ: 61728.
7. *Решите уравнение: $20:(33-4 \cdot x)+47=51$
   Решение:
   $20 : (33 - 4x) = 4$;
   $33 - 4x = 5$;
   $4x = 28$;
   $x = 7$.
   Ответ: 7.
8. Расставьте между числами знаки действий и скобки так, чтобы получилось верное равенство: $6\ 8\ 20\ 4\ 2 =58$
   Решение: Например, $6 \cdot 8 + 20 : (4 - 2) = 48 + 10 = 58$.
   Ответ: $6 \cdot 8 + 20 : (4 - 2) = 58$.
9. Расставьте в клетках данной таблицы числа 0, 1, 2, 3, 4, 5, 6, 7, 8 (по одному каждое) так, чтобы сумма чисел в каждой строке, каждом столбце и на двух главных диагоналях была одинаковой.
   Решение: Пример заполнения:
   
   Сумма в каждой линии: 12.
10. *Найдите периметр и площадь прямоугольника, у которого длина 18 см, и она больше ширины на 5 см.
    Решение:
    Ширина: $18 - 5 = 13$ см.
    Периметр: $2 \cdot (18 + 13) = 62$ см.
    Площадь: $18 \cdot 13 = 234$ см².
    Ответ: 234 см², 62 см.
11. *Муха летит со скоростью 5 м/с. Сколько километров она пролетит за час?
    Решение:
    $5 \cdot 3600 = 18000$ м = 18 км.
    Ответ: 18 км.
12. *Шапокляк и Крокодил Гена едут по одной дороге в одном направлении. Сейчас между ними 105 км. Какова скорость Крокодила, если Шапокляк, скорость которой 90 км/ч, догнала его через 3 часа?
    Решение:
    Скорость сближения: $\frac{105}{3} = 35$ км/ч.
    Скорость Гены: $90 - 35 = 55$ км/ч.
    Ответ: 55 км/ч.
13. Марина ходит в спортзал один раз в 6 дней, Маша – один раз в 3 дня, а Катя – один раз в 4 дня. Они встретились в спортзале в субботу. В какой день недели они встретятся вновь?
    Решение: НОК(6, 3, 4) = 12 дней. Суббота + 12 дней = четверг.
    Ответ: в четверг.
14. *На какую цифру оканчивается разность $4 \cdot 14 \cdot 24 \cdot \ldots \cdot 20124-1 ?$
    Решение: Все множители оканчиваются на 4. Произведение нечетного количества таких чисел оканчивается на 4. Тогда $4 - 1 = 3$.
    Ответ: на 3.
15. *Сколько различных трехзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая из этих цифр может быть использована только один раз?
    Решение: Первая цифра: 1 или 3 (2 варианта). Остальные две цифры выбираются из 4 оставшихся: $2 \cdot 4 \cdot 3 = 24$.
    Ответ: 24.