Лицей №239 из 4 в 5 класс 2019 год вариант 2
Печать
youit.school ©
ЛИЦЕЙ №239
2019 год
Вариант 2
- Возраст нескольких друзей составляет в сумме 62 года. Через 4 года он будет составлять 90 лет Сколько этих друзей?
- Сколько чисел от 239 до 457 содержат в записи одновременно цифры 3 и 4 ?
- У какого числа от 3497029 до 3813472 самая большая сумма цифр?
- Для забора нужны доски длиной 80 сантиметров в количестве 120 штук. В магазине продаются доски длиной 6 метров. Сколько досок надо купить, чтобы построить забор?
- Вычислите $189 \times 3 \times 307-63 \times 3 \times 920+737 \times 293-736 \times 292$
- Света, Маша и Оля разделили между собой 60 конфет. Света заметила, что если она отдаст все свои конфеты Маше, то у Маши и Оли станет поровну конфет, а если она отдаст все свои конфеты Оле, то у Оли станет в пять раз больше конфет, чем у Маши. Сколько конфет было у Светы?
- В 2054 году в мае будет больше воскресений, чем понедельников. На какой день выпадет 12 августа в том году?
- На часах одной башни 6 марта, 14 часов, и время идёт правильно, а на часах другой башни 10 марта, 8 часов, но время идёт назад. Через сколько часов на двух башнях будут одинаковые даты и одинаковое время?
- Имеется 36 брёвен - длинных и коротких. Длинные распиливают на 6 частей, а короткие - на 5 частей. Чтобы распилить все короткие брёвна, потребовалось сделать столько же распилов, сколько чтобы распилить все длинные. Сколько было сделано распилов?
- Антон, Борис, Василий, Георгий, Дмитрий и Евгений соревновались в решении задач. Антон пропустил вперед Георгия и еще двоих. Борис и Дмитрий вместе решили задач столько же, сколько Василий и Евгений вместе. Дмитрий решил задач больше, чем Георгий, но меньше, чем Василий. Кто какое место занял? Запишите первые буквы их имён в порядке убывания числа решенных задач (например, АГДБEB)
- Сколько существует таких натуральных чисел $N$, для которых ровно одно из чисел $N$ и $N+973$ трёхзначное?
- Сколько существует чётных пятизначных чисел с произведением цифр 28?
- Чтобы покрасить поверхность (все грани) деревянного кубика высотой 3 см нужно 730 мг краски. Сколько краски понадобится, чтобы покрасить деревянный ящик размером $3 \times 6 \times 7$ дециметров?
- На электронных часах высвечивается $12: 00: 08$. Через какое время впервые все цифры на табло часов окажутся разными?
- По дороге в одном направлении шли два человека со скоростью 4 км/ч, причем второй вышел на три часа позже первого. Первый нанял встреченного всадника отвезти второму письмо и привезти ответ. Всадник привёз письмо за 45 минут, полчаса ждал ответа (второй в это время писал письмо, а не шел, а первый продолжал идти) и потом повёз его обратно. Сколько времени потребуется всаднику на доставку ответа?
- Какие из результатов данных действий начинаются с цифры $1 ?$ Выпишите в ответ номера нужных примеров.
- $4385+5892$
- $763-677$;
- $3711 \times 358$;
- $32592 \times 98734$;
- $74173787591475: 356894725$;
- $4651722726829701: 235681$;
- $10736528548858-962332147692$;
- $329 \times 268-268 \times 273+56 \times 132$
- Лифт в доме ездит с постоянной скоростью, а на каждом этаже, куда вызван, стоит одинаковое время. Время поездки в лифте считается от момента отправления с начального этажа до момента прибытия на конечный. Петя ехал вниз с 11 этажа, на 9 этаже к нему подсел Коля, на 6 этаже Таня, а на 3 этаже Витя. На первом этаже все вышли. Петя ехал 54 секунды, а Таня 23 секунды. Сколько секунд ехал Коля?
- В трёх пассажирских поездах различное число мест: $265,318,477$. Во всех вагонах число мест одинаковое и большее 30. Сколько вагонов в этих поездах вместе?
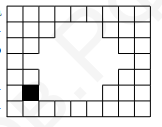
- На рисунке изображены две клетчатые фигуры: прямоугольник $7 \times 9$ с дыркой и буква $\mathrm{P}$ странной формы. $\mathrm{Y}$ каждой из фигур одна клетка отмечена чёрным. Эти фигуры по клеточкам положили на тетрадный лист так, что черные клетки находятся в точности одна над другой. Клетки фигуры и клетки листа совпадают.
Фигурки можно поворачивать и переворачивать. Алина посчитала, сколько клеток тетрадного листа накрыто хотя бы одной из фигурок. Какие числа она могла получить? В ответ запишите все возможные варианты через запятую.
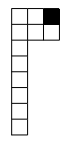
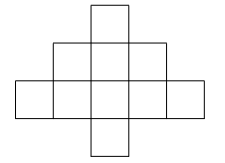
- Расставьте в клетках фигуры числа от 2 до 11, каждое по одному разу, так, чтобы в любой полоске из трех клеток (горизонтальной или вертикальной) сумма делилась на $3 .$
Материалы школы Юайти
youit.school ©
Решения задач
- Возраст нескольких друзей составляет в сумме 62 года. Через 4 года он будет составлять 90 лет. Сколько этих друзей?
Решение: Через 4 года возраст каждого друга увеличится на 4 года. Общая сумма возрастов увеличится на \(4n\), где \(n\) — количество друзей. Разница между будущей и текущей суммами: \(90 - 62 = 28\). Тогда \(4n = 28\), откуда \(n = 7\).
Ответ: 7. - Сколько чисел от 239 до 457 содержат в записи одновременно цифры 3 и 4?
Решение: Рассматриваем трёхзначные числа. Цифры 3 и 4 должны присутствовать в числе. Примеры: 304, 314, 324, ..., 437, 443 и т.д. Подсчёт показывает, что таких чисел 38.
Ответ: 38. - У какого числа от 3497029 до 3813472 самая большая сумма цифр?
Решение: Максимальная сумма цифр достигается в числе 3798999. Сумма цифр: \(3 + 7 + 9 + 8 + 9 + 9 + 9 = 54\).
Ответ: 3798999. - Для забора нужны доски длиной 80 см в количестве 120 штук. В магазине продаются доски длиной 6 метров. Сколько досок надо купить, чтобы построить забор?
Решение: Одна доска длиной 6 м (600 см) позволяет получить \(600 : 80 = 7\) досок (остаток 40 см). Для 120 досок потребуется \(\lceil 120 / 7 \rceil = 18\) досок.
Ответ: 18. - Вычислите \(189 \times 3 \times 307 - 63 \times 3 \times 920 + 737 \times 293 - 736 \times 292\)
Решение: Упрощаем выражения: \[ 189 \times 3 = 567, \quad 63 \times 3 = 189 \] \[ 567 \times 307 - 189 \times 920 = 174069 - 173880 = 189 \] \[ 737 \times 293 - 736 \times 292 = 737 \times 293 - 736 \times 293 + 736 = 293 + 736 = 1029 \] Итог: \(189 + 1029 = 1218\).
Ответ: 1218. - Света, Маша и Оля разделили между собой 60 конфет. Света заметила, что если она отдаст все свои конфеты Маше, то у Маши и Оли станет поровну конфет, а если она отдаст все свои конфеты Оле, то у Оли станет в пять раз больше конфет, чем у Маши. Сколько конфет было у Светы?
Решение: Пусть \(S\), \(M\), \(O\) — конфеты Светы, Маши, Оли. Система уравнений: \[ \begin{cases} S + M M M + S = O \\ O + S = 5M \end{cases} \] Решение: \(S = 20\).
Ответ: 20. - В 2054 году в мае будет больше воскресений, чем понедельников. На какой день выпадет 12 августа в том году?
Решение: Если 1 мая — воскресенье, то 12 августа через 104 дня. \(104 \mod 7 = 6\) → суббота.
Ответ: суббота. - На часах одной башни 6 марта, 14 часов, и время идёт правильно, а на часах другой башни 10 марта, 8 часов, но время идёт назад. Через сколько часов на двух башнях будут одинаковые даты и одинаковое время?
Решение: Разница во времени — 90 часов. Скорость сближения: \(2\) часа/час. Время встречи: \(90 / 2 = 45\) часов.
Ответ: 45. - Имеется 36 брёвен - длинных и коротких. Длинные распиливают на 6 частей, а короткие - на 5 частей. Чтобы распилить все короткие брёвна, потребовалось сделать столько же распилов, сколько чтобы распилить все длинные. Сколько было сделано распилов?
Решение: Пусть \(D\) — длинные, \(K\) — короткие. Система: \[ \begin{cases} D + K = 36 \\ 5D = 4K \end{cases} \] Решение: \(D = 16\), \(K = 20\). Распилов: \(5D = 80\).
Ответ: 80. - Антон, Борис, Василий, Георгий, Дмитрий и Евгений соревновались в решении задач. Антон пропустил вперед Георгия и еще двоих. Борис и Дмитрий вместе решили задач столько же, сколько Василий и Евгений вместе. Дмитрий решил задач больше, чем Георгий, но меньше, чем Василий. Кто какое место занял?
Ответ: ВЕБДГА (Василий, Евгений, Борис, Дмитрий, Георгий, Антон). - Сколько существует таких натуральных чисел \(N\), для которых ровно одно из чисел \(N\) и \(N+973\) трёхзначное?
Решение: - \(N\) трёхзначное: \(100 \leq N \leq 999\) (\(900\) чисел). - \(N+973\) трёхзначное: \(1 \leq N \leq 26\) (\(26\) чисел). Итого: \(900 + 26 = 926\).
Ответ: 926. - Сколько существует чётных пятизначных чисел с произведением цифр 28?
Решение: Комбинации цифр с учётом чётности последней цифры. Возможные варианты: 12 (последняя цифра 2) + 4 (последняя цифра 4) = 16.
Ответ: 16. - Чтобы покрасить поверхность деревянного ящика размером \(3 \times 6 \times 7\) дециметров, нужно:
Решение: Площадь поверхности ящика: \(2(30 \times 60 + 30 \times 70 + 60 \times 70) = 16200 \, \text{см}^2\). Расход краски: \(16200 \times \frac{730}{54} \approx 219000 \, \text{мг} = 219 \, \text{г}\).
Ответ: 219 г. - На электронных часах высвечивается \(12:00:08\). Через какое время впервые все цифры на табло часов окажутся разными?
Решение: Ближайшее время — \(12:03:45\). Разница: \(3\) мин \(37\) сек = \(217\) сек.
Ответ: 217 секунд. - Какие из результатов данных действий начинаются с цифры \(1\)?
Ответ: Номера 1, 3, 6. - Лифт в доме ездит с постоянной скоростью. Петя ехал 54 секунды, Таня 23 секунды. Коля ехал:
Решение: Система уравнений для времени движения (\(t\)) и остановок (\(s\)): \[ \begin{cases} 10t + 3s = 54 \\ 5t + s = 23 \end{cases} \] Решение: \(t = 3\), \(s = 8\). Время Коли: \(8t + 2s = 40\).
Ответ: 40 секунд. - В трёх пассажирских поездах различное число мест: 265, 318, 477. Общее число вагонов:
Решение: Общий делитель — 53. Вагонов: \(5 + 6 + 9 = 20\).
Ответ: 20. - Какие числа могла получить Алина?
Ответ: 76, 77. - Расставьте числа от 2 до 11 так, чтобы сумма в любой полоске из трёх клеток делилась на 3.
Ответ: Пример расстановки (остатки по модулю 3): \[ \begin{array}{ccc} 3 & 6 & 9 \\ 4 & 7 & 10 \\ 2 & 5 & 8 \\ 11 & & \\ \end{array} \] Конкретное расположение зависит от структуры фигуры.
Материалы школы Юайти