8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 4 в 5 класс 2009 год (вариант 2)

Сложность:
Дата экзамена: 2009
Сложность:
Дата экзамена: 2009
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239


2009 год


Вариант 2




  1. Запишите цифрами число сто тысяч восемьсот пять.
  2. Сколько нечётных чисел в этом ряду: $16,27,258,2667,8888 ?$
  3. Найдите неизвестное значение компоненты $((239+x): 3-438) \cdot 25-116=2009$
  4. Волк бежит за зайцем. Волк пробегает 200 метров в минуту, а заяц - 160 метров в минуту. Через сколько минут волк догонит зайца, если сейчас между ними 200 метров?
  5. Какое самое большое четное число можно составить из цифр 2, 4, 8 и 9, если каждую цифру надо использовать точно один раз?
  6. Периметр прямоугольника равен 30 см, а одна из его сторон равна 5 см. Чему равна другая его сторона?
  7. Лещ весит 2 кг и ещё поллеща. Сколько весят 2 одинаковых леща?
  8. Веревку длиной 45 метров разрезали на два куска, один из которых вчетверо длиннее другого. Какова длина большего куска?
  9. Расставьте скобки так, чтобы равенство было верным: $20: 2+7 \cdot 2-5=29$
  10. Какое число надо разделить на 5 , чтобы получилось произведение чисел 10 и 2 ?
  11. Как 55 орехов разложить на 10 тарелок так, чтобы в каждой было разное количество орехов?
  12. Из двух одинаковых квадратов сложили прямоугольник. Чему равна площадь прямоугольника, если периметр одного квадрата 16 дм?
  13. Для похода 46 лицеистов приготовили шестиместные и четырёхместные лодки. Сколько было тех и других лодок, если все ребята разместились в 10 лодках и свободных мест не осталось?
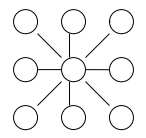
  14. Разместите числа $2,3,4,5,6,7,8,9,10$ в пустых кружках так, чтобы сумма трёх чисел, расположенных на каждой прямой, была равна $18 .$ (см. рисунок слева)
  15. Поезд должен пройти 700 км за 9 часов. Первые 3 часа он шёл со скоростью 70 км/ч, следующие 2 часа - со скоростью 85 км/ч. С какой скоростью он должен идти оставшийся путь, чтобы прийти в пункт назначения по расписанию?
  16. В году 150 учебных дней. Каждый из 5 классов решали по 3 задачи за урок. Сколько всего задач было решено за год, если по субботам уроков математики не было?
  17. На день рождения Вини-Пух получил от Кролика 1 кг 80 г мёда, а от Пятачка- в 3 раза меньше. Весь мёд был в одинаковых банках, которых Кролик дал на 8 больше, чем Пятачок. Сколько банок мёда получил Пух?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Запишите цифрами число сто тысяч восемьсот пять.
    Решение: Сто тысяч восемьсот пять = 100000 + 800 + 5 = 100805.
    Ответ: 100805.
  2. Сколько нечётных чисел в этом ряду: $16,27,258,2667,8888$?
    Решение: Нечётные числа оканчиваются на 1, 3, 5, 7, 9. В ряду нечётными являются числа 27 и 2667.
    Ответ: 2 числа.
  3. Найдите неизвестное значение компоненты $((239+x): 3-438) \cdot 25-116=2009$.
    Решение:
    $((239+x):3 - 438) \cdot 25 = 2009 + 116 = 2125$
    $(239+x):3 - 438 = 2125 : 25 = 85$
    $(239+x):3 = 85 + 438 = 523$
    $239 + x = 523 \cdot 3 = 1569$
    $x = 1569 - 239 = 1330$
    Ответ: 1330.
  4. Волк бежит за зайцем. Волк пробегает 200 метров в минуту, а заяц - 160 метров в минуту. Через сколько минут волк догонит зайца, если сейчас между ними 200 метров?
    Решение: За 1 минуту волк сокращает расстояние на $200 - 160 = 40$ метров. Для преодоления 200 метров потребуется $200 : 40 = 5$ минут.
    Ответ: 5 минут.
  5. Какое самое большое четное число можно составить из цифр 2, 4, 8 и 9, если каждую цифру надо использовать точно один раз?
    Решение: Наибольшее чётное число получится, если последней цифрой поставить 8. Остальные цифры располагаем в порядке убывания: 9, 4, 2. Получаем 9842.
    Ответ: 9842.
  6. Периметр прямоугольника равен 30 см, а одна из его сторон равна 5 см. Чему равна другая его сторона?
    Решение: Полупериметр равен $30 : 2 = 15$ см. Другая сторона: $15 - 5 = 10$ см.
    Ответ: 10 см.
  7. Лещ весит 2 кг и ещё поллеща. Сколько весят 2 одинаковых леща?
    Решение: Пусть лещ весит $x$ кг. Тогда $x = 2 + 0,5x$, откуда $x = 4$ кг. Два леща весят $4 \cdot 2 = 8$ кг.
    Ответ: 8 кг.
  8. Веревку длиной 45 метров разрезали на два куска, один из которых вчетверо длиннее другого. Какова длина большего куска?
    Решение: Меньший кусок — $x$, больший — $4x$. Сумма: $x + 4x = 45$, откуда $x = 9$ м. Больший кусок: $4 \cdot 9 = 36$ м.
    Ответ: 36 метров.
  9. Расставьте скобки так, чтобы равенство было верным: $20: 2+7 \cdot 2-5=29$.
    Решение: $(20 : 2 + 7) \cdot 2 - 5 = (10 + 7) \cdot 2 - 5 = 34 - 5 = 29$.
    Ответ: $(20 : 2 + 7) \cdot 2 - 5 = 29$.
  10. Какое число надо разделить на 5 , чтобы получилось произведение чисел 10 и 2?
    Решение: Искомое число равно $10 \cdot 2 \cdot 5 = 100$.
    Ответ: 100.
  11. Как 55 орехов разложить на 10 тарелок так, чтобы в каждой было разное количество орехов?
    Решение: Числа от 1 до 10 в сумме дают $1+2+3+\dots+10 = 55$. Распределение: 1, 2, 3, ..., 10 орехов.
    Ответ: 1, 2, 3, ..., 10 орехов.
  12. Из двух одинаковых квадратов сложили прямоугольник. Чему равна площадь прямоугольника, если периметр одного квадрата 16 дм?
    Решение: Сторона квадрата: $16 : 4 = 4$ дм. Прямоугольник имеет размеры $4 \times 8$ дм. Площадь: $4 \cdot 8 = 32$ дм².
    Ответ: 32 дм².
  13. Для похода 46 лицеистов приготовили шестиместные и четырёхместные лодки. Сколько было тех и других лодок, если все ребята разместились в 10 лодках и свободных мест не осталось?
    Решение: Пусть $x$ — шестиместные, $y$ — четырёхместные. Система:
    $\begin{cases} x + y = 10 \\ 6x + 4y = 46 \end{cases}$
    Решение: $x = 3$, $y = 7$.
    Ответ: 3 шестиместные и 7 четырёхместных.
  14. Разместите числа $2,3,4,5,6,7,8,9,10$ в пустых кружках так, чтобы сумма трёх чисел, расположенных на каждой прямой, была равна $18$.
    Решение: Центральное число — 6. Пары: 2+10, 3+9, 4+8, 5+7. Распределение по линиям:
    $2-6-10$, $3-6-9$, $4-6-8$, $5-6-7$.
  15. Поезд должен пройти 700 км за 9 часов. Первые 3 часа он шёл со скоростью 70 км/ч, следующие 2 часа - со скоростью 85 км/ч. С какой скоростью он должен идти оставшийся путь, чтобы прийти в пункт назначения по расписанию?
    Решение: Пройдено: $3 \cdot 70 + 2 \cdot 85 = 380$ км. Осталось: $700 - 380 = 320$ км. Время: $9 - 3 - 2 = 4$ часа. Скорость: $320 : 4 = 80$ км/ч.
    Ответ: 80 км/ч.
  16. В году 150 учебных дней. Каждый из 5 классов решали по 3 задачи за урок. Сколько всего задач было решено за год, если по субботам уроков математики не было?
    Решение: Учебных недель: $150 : 6 = 25$. Уроков в неделю: 5 дней. Задачи одного класса: $25 \cdot 5 \cdot 3 = 375$. Всего: $375 \cdot 5 = 1875$.
    Ответ: 1875.
  17. На день рождения Вини-Пух получил от Кролика 1 кг 80 г мёда, а от Пятачка- в 3 раза меньше. Весь мёд был в одинаковых банках, которых Кролик дал на 8 больше, чем Пятачок. Сколько банок мёда получил Пух?
    Решение: Кролик подарил 1080 г, Пятачок — 360 г. Разница: 720 г = 8 банок. Масса банки: $720 : 8 = 90$ г. Кролик дал $1080 : 90 = 12$ банок, Пятачок — 4 банки. Всего: $12 + 4 = 16$ банок.
    Ответ: 16 банок.
Материалы школы Юайти