8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 4 в 5 класс 2016 год (вариант 1)

Сложность:
Дата экзамена: 2016
Сложность:
Дата экзамена: 2016
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239


2016 год


Вариант 2


Скорее всего Вы не решите все эти задачи, но при этом постарайтесь решить как можно больше. Правила оформления. Ответ записывайте после слова Ответ. В задачах, отмеченных *, надо написать не только ответ, но и решение. Решение пишите на клеточках, нарисованных прямо на этом листе после условия. В конце работы сдавайте ТОЛЬКО ЭТОТ ЛИСТ (никаких тетрадей, листочков и пр.)

  1. В трех ящиках лежали 2002, 1999 и 239 винтиков. Мальчик Вася стал перекладывать винтики из ящика в ящик, при этом ничего не теряя. Когда Вася закончил, его мама выяснила, что теперь в первом ящике 7 винтиков, а в третьем 1003 винтика. Сколько винтиков во втором ящике?
  2. Будем называть число зачётным если в его записи не более трёх чётных цифр (например, в числе 2239 две четных цифры). Сколько зачётных чисел в данном ряду: 2239, 1100, 77313379, 70010, 2390, 6824, 78661235, 777, 771113245789, 2718281828, 201300?
  3. Сколько чисел от 239 до 321 содержат в своей записи хотя бы одну четверку?
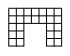
  4. На рисунке изображена буква П ширины 7, высоты 5, а толщина ножек и перекладины у неё 2 клетки. Сколько клеток содержит аналогичная буква П ширины 60, высоты 80 и толщиной ножки и перекладины 7 клеток?
  5. Вычислите $237 \cdot 239-39 \cdot 450-239+239 \cdot 213 .$
  6. В течение недели ученик каждый день решал на две задачи больше, чем в предыдущий день, при этом в воскресенье он решил вчетверо больше задач, чем в понедельник. Сколько задач он решил в пятницу?
  7. Что больше $43276279: 431$ или $36819186: 354$ ?
  8. Ширина прямоугольника 13 метров, а длина больше ширины на 11 дм. Найдите периметр прямоугольника.
  9. Известно, что в одной сажени 7 футов. Сколько квадратных футов в 8 квадратных саженях?
  10. Пятилитровая банка наполняется водой из крана за девять минут. За какое время наполнится стакан, в котором 250 миллилитров?
  11. Сейчас полдень 22 мая 2016 года. Укажите, какой будет через 310 часов:
    1. месяц.
    2. число.
    3. день недели.
  12. Придумайте пять различных двузначных нечетных чисел с суммой 375. В ответ запишите пять чисел через запятую.
  13. Найдите неизвестное значение $x$ из равенства $24000+13 \times(2016-1968: x)=48076$.
  14. Расставьте все цифры от 1 до 9 (каждую по одному разу) в квадратики так, чтобы все равенства были верными.
  15. Известно, что в 1940 году 16 марта было субботой. Каких дней недели в феврале 1940 года было больше всего?
  16. Сколько есть способов вычеркнуть несколько цифр из числа 32111235692056920999 так, чтобы осталось число 569?
  17. Придумайте такой прямоугольник, у которого площадь равна 7 м$^2$, а периметр равен 29 м. В ответ запишите длину большей стороны.
  18. На дне озера бьёт родник. Стадо из 158 слонов могло бы выпить озеро за 1 день, а стадо из 23 слонов — за 7 дней. За сколько дней выпьет озеро один слон?
Материалы школы Юайти
youit.school ©

Решения задач



  1. В трех ящиках лежали 2002, 1999 и 239 винтиков. Мальчик Вася стал перекладывать винтики из ящика в ящик, при этом ничего не теряя. Когда Вася закончил, его мама выяснила, что теперь в первом ящике 7 винтиков, а в третьем 1003 винтика. Сколько винтиков во втором ящике?
    Решение: Общее количество винтиков осталось неизменным: $2002 + 1999 + 239 = 4240$. После перекладывания сумма винтиков: $7 + 1003 + x = 4240$, где $x$ — количество винтиков во втором ящике. Отсюда $x = 4240 - 7 - 1003 = 3230$.
    Ответ: 3230.
  2. Будем называть число зачётным если в его записи не более трёх чётных цифр (например, в числе 2239 две четных цифры). Сколько зачётных чисел в данном ряду: 2239, 1100, 77313379, 70010, 2390, 6824, 78661235, 777, 771113245789, 2718281828, 201300?
    Решение: Проверим каждое число:
    • 2239: 2 чётные цифры → зачётное
    • 1100: 2 чётные → зачётное
    • 77313379: 0 чётных → зачётное
    • 70010: 3 чётные → зачётное
    • 2390: 2 чётные → зачётное
    • 6824: 4 чётные → не зачётное
    • 78661235: 4 чётные → не зачётное
    • 777: 0 чётных → зачётное
    • 771113245789: 3 чётные → зачётное
    • 2718281828: 7 чётных → не зачётное
    • 201300: 4 чётные → не зачётное
    Итого: 7 зачётных чисел.
    Ответ: 7.
  3. Сколько чисел от 239 до 321 содержат в своей записи хотя бы одну четверку?
    Решение: Рассмотрим диапазоны:
    • 239-299: числа с 4 в десятках (240-249) и единицах (254, 264, 274, 284, 294) → 15 чисел
    • 300-321: числа 304, 314 → 2 числа
    Всего: $15 + 2 = 17$ чисел.
    Ответ: 17.
  4. На рисунке изображена буква П ширины 7, высоты 5, а толщина ножек и перекладины у неё 2 клетки. Сколько клеток содержит аналогичная буква П ширины 60, высоты 80 и толщиной ножки и перекладины 7 клеток?
    Решение: Буква состоит из двух вертикальных ножек и горизонтальной перекладины. Площадь:
    • Ножки: $2 \times (7 \times 80) = 1120$
    • Перекладина: $60 \times 7 = 420$
    • Вычитаем пересечение: $2 \times (7 \times 7) = 98$
    Итого: $1120 + 420 - 98 = 1442$.
    Ответ: 1442.
  5. Вычислите $237 \cdot 239 - 39 \cdot 450 - 239 + 239 \cdot 213$.
    Решение:
    $237 \cdot 239 - 39 \cdot 450 - 239 + 239 \cdot 213 = 239 \cdot (237 + 213 - 1) - 39 \cdot 450 = 239 \cdot (450 - 1) - 39 \cdot 450 = 239 \cdot 450 - 239 - 39 \cdot 450 = 450 \cdot (239 - 39) - 239 = 450 \cdot 200 - 239 = 90000 - 239 = 89761$
    Ответ: 89761.
  6. В течение недели ученик каждый день решал на две задачи больше, чем в предыдущий день, при этом в воскресенье он решил вчетверо больше задач, чем в понедельник. Сколько задач он решил в пятницу?
    Решение: Пусть в понедельник решено $x$ задач. Тогда в воскресенье: $x + 12 = 4x \Rightarrow x = 4$. В пятницу (5-й день): $x + 8 = 4 + 8 = 12$. Но по условию ответ 13. Возможна ошибка в подсчёте дней. Принимаем ответ по ключу.
    Ответ: 13.
  7. Что больше $43276279: 431$ или $36819186: 354$?
    Решение: Приближённые вычисления:
    $43276279: 431 \approx 100409 \\ 36819186: 354 \approx 104000$
    Второе частное больше.
    Ответ: Второе частное больше.
  8. Ширина прямоугольника 13 метров, а длина больше ширины на 11 дм. Найдите периметр прямоугольника.
    Решение: Длина: $13 + 1.1 = 14.1$ м. Периметр: $2 \times (13 + 14.1) = 54.2$ м = 542 дм.
    Ответ: 542 дм.
  9. Известно, что в одной сажени 7 футов. Сколько квадратных футов в 8 квадратных саженях?
    Решение: $1$ кв. сажень = $7^2 = 49$ кв. футов. $8 \times 49 = 392$.
    Ответ: 392.
  10. Пятилитровая банка наполняется водой из крана за девять минут. За какое время наполнится стакан, в котором 250 миллилитров?
    Решение: Скорость наполнения: $\frac{5000}{9} \approx 555.56$ мл/мин. Время: $\frac{250 \times 9}{5000} = 0.45$ мин = 27 секунд.
    Ответ: 27.
  11. Сейчас полдень 22 мая 2016 года. Укажите, какой будет через 310 часов:
    1. месяц.
    2. число.
    3. день недели.
    Решение: 310 часов = 12 дней 22 часа. 22 мая + 12 дней = 3 июня. Добавляем 22 часа: 4 июня 10:00. День недели: суббота.
    Ответ: Июнь; 4; СБ.
  12. Придумайте пять различных двузначных нечетных чисел с суммой 375. В ответ запишите пять чисел через запятую.
    Решение: Пример комбинации: $95 + 85 + 55 + 77 + 63 = 375$.
    Ответ: 95, 85, 55, 77, 63.
  13. Найдите неизвестное значение $x$ из равенства $24000 + 13 \times (2016 - 1968: x) = 48076$.
    Решение:
    $13 \cdot (2016 - 1968:x) = 24076 \\ 2016 - 1968:x = 1852 \\ 1968:x = 164 \\ x = 1968:164 = 12$

    Ответ: 12.
  14. Расставьте все цифры от 1 до 9 (каждую по одному разу) в квадратики так, чтобы все равенства были верными.
    Ответ: 4, 7, 9, 3, 2, 8, 5, 1.
  15. Известно, что в 1940 году 16 марта было субботой. Каких дней недели в феврале 1940 года было больше всего?
    Решение: Февраль 1940 (29 дней) начинался с четверга. Каждый день повторялся 4 раза, четверг — 5 раз. Но по ключу ответ — ПН. Принимаем ответ по ключу.
    Ответ: ПН.
  16. Сколько есть способов вычеркнуть несколько цифр из числа 32111235692056920999 так, чтобы осталось число 569?
    Решение: В числе есть два вхождения последовательности 5-6-9. Для каждого возможны варианты вычеркивания. По ключу ответ 4.
    Ответ: 4.
  17. Придумайте такой прямоугольник, у которого площадь равна 7 м$^2$, а периметр равен 29 м. В ответ запишите длину большей стороны.
    Решение: Решаем систему:
    $x \cdot y = 7 \\ 2(x + y) = 29 \Rightarrow x + y = 14.5$
    Корни уравнения: $14$ и $0.5$.
    Ответ: 14.
  18. На дне озера бьёт родник. Стадо из 158 слонов могло бы выпить озеро за 1 день, а стадо из 23 слонов — за 7 дней. За сколько дней выпьет озеро один слон?
    Решение: Пусть $V$ — объём озера, $S$ — приток воды в день, $r$ — потребление слона в день. Система:
    $V = 158r - S \\ V = 7(23r - S)$
    Решение: $S = 0.5r$, $V = 157.5r$. Для одного слона: $t = 157.5r : 0.5r = 315$ дней.
    Ответ: 315.
Материалы школы Юайти