Лицей №239 из 4 в 5 класс 2012 год (вариант 1)

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239

2012 год

Вариант 1

В задачах, отмеченных *, требуется записать решение, а не только ответ!

1. Сколько натуральных чисел от 10 до 110 делится на 2?
2. Какова разность между наибольшим и наименьшим четырехзначными числами, все цифры которых различны?
3. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее количество шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и членов команды?
4. *В 4 классе 35 учеников. В течение учебного дня 20 человек питаются бутербродами, 11 человек посещают кафе, 10 человек голодают. Сколько человек съедает бутерброды, сидя в кафе?
5. Встретились три друга: Белов, Чернов и Рыжов. Один из них блондин, другой брюнет, а третий рыжий. Брюнет сказал Белову: «Ни у кого из нас цвет волос не соответствует фамилии". Какой цвет волос у каждого из них?
6. *Вычислите: $(23199: 57-22557: 73) \cdot 467$
7. *Решите уравнение: $(9 \cdot x-18): 7+14=23$
8. Расставьте между цифрами знаки действий и скобки так, чтобы получилось верное равенство:
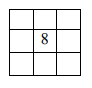
   5 4 3 2 1 = 100
9. Расставьте в клетках данной таблицы числа 4, 5, 6, 7, 9, 10, 11, 12 (по одному каждое) так, чтобы сумма чисел в каждой строке, каждом столбце и на двух главных диагоналях была равна 24.
   
10. *Найдите периметр и площадь прямоугольника, у которого ширина 12 см, и она меньше длины на 4 см.
11. *Скорость стрекозы 15 м/с, а скорость шмеля 60 км/ч. Кто из них летит быстрее?
12. *Два бобра одновременно с двух концов начали грызть осиновый ствол. Один бобер грыз со скоростью 55 см/ч, а другой - со скоростью 65 см/ч. Определите длину ствола, если за 2ч 30 мин он был изгрызен полностью.
13. Петя ходит в бассейн один раз в 2 дня, Коля – один раз в 4 дня, а Вова – один раз в 5 дней. Они встретились в бассейне во вторник. В какой день недели они встретятся вновь?
14. *На какую цифру оканчивается сумма $9 \cdot 19 \cdot 29 \cdot \ldots \cdot 20129+1 ?$
15. *Сколько существует пятизначных чисел, у которых третья цифра 7, а последняя цифра четная?

Решения задач

1. Сколько натуральных чисел от 10 до 110 делится на 2?
   Решение: Первое четное число в диапазоне — 10, последнее — 110. Количество чисел: $\frac{110 - 10}{2} + 1 = \frac{100}{2} + 1 = 50 + 1 = 51$.
   Ответ: 51.
2. Какова разность между наибольшим и наименьшим четырехзначными числами, все цифры которых различны?
   Решение: Наибольшее число — 9876, наименьшее — 1023. Разность: $9876 - 1023 = 8853$.
   Ответ: 8853.
3. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее количество шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и членов команды?
   Решение: Всего людей: $750 + 25 = 775$. Количество шлюпок: $\lceil \frac{775}{70} \rceil = \lceil 11,07 \rceil = 12$.
   Ответ: 12 шлюпок.
4. *В 4 классе 35 учеников. В течение учебного дня 20 человек питаются бутербродами, 11 человек посещают кафе, 10 человек голодают. Сколько человек съедает бутерброды, сидя в кафе?
   Решение: По принципу включения-исключения: $20 + 11 + 10 - 35 = 6$ человек пересекаются.
   Ответ: 6 человек.
5. Встретились три друга: Белов, Чернов и Рыжов. Один из них блондин, другой брюнет, а третий рыжий. Брюнет сказал Белову: «Ни у кого из нас цвет волос не соответствует фамилии". Какой цвет волос у каждого из них?
   Решение: Брюнет не может быть Черновым, значит брюнет — Рыжов. Белов не брюнет и не рыжий (по условию), значит Белов — рыжий. Чернов — блондин.
   Ответ: Белов — рыжий, Чернов — блондин, Рыжов — брюнет.
6. *Вычислите: $(23199: 57-22557: 73) \cdot 467$
   Решение: $23199 : 57 = 407$, $22557 : 73 = 309$, $407 - 309 = 98$, $98 \cdot 467 = 45766$.
   Ответ: 45766.
7. *Решите уравнение: $(9 \cdot x-18): 7+14=23$
   Решение: $(9x - 18) : 7 = 9$, $9x - 18 = 63$, $9x = 81$, $x = 9$.
   Ответ: 9.
8. Расставьте между цифрами знаки действий и скобки так, чтобы получилось верное равенство:
   5 4 3 2 1 = 100
   Решение: $5 \cdot 4 \cdot (3 \cdot 2 - 1) = 100$.
   Ответ: $5 \cdot 4 \cdot (3 \cdot 2 - 1) = 100$.
9. Расставьте в клетках данной таблицы числа 4, 5, 6, 7, 9, 10, 11, 12 (по одному каждое) так, чтобы сумма чисел в каждой строке, каждом столбце и на двух главных диагоналях была равна 24.
   Пример решения:
   Ответ: Указанная таблица.
10. *Найдите периметр и площадь прямоугольника, у которого ширина 12 см, и она меньше длины на 4 см.
    Решение: Длина: $12 + 4 = 16$ см. Периметр: $2 \cdot (12 + 16) = 56$ см. Площадь: $12 \cdot 16 = 192$ см².
    Ответ: $192 \mathrm{~cm}^{2}, 56 \mathrm{~cm}$.
11. *Скорость стрекозы 15 м/с, а скорость шмеля 60 км/ч. Кто из них летит быстрее?
    Решение: $60$ км/ч = $\frac{60 \cdot 1000}{3600} \approx 16,67$ м/с. Шмель быстрее.
    Ответ: шмель.
12. *Два бобра одновременно с двух концов начали грызть осиновый ствол. Один бобер грыз со скоростью 55 см/ч, а другой - со скоростью 65 см/ч. Определите длину ствола, если за 2ч 30 мин он был изгрызен полностью.
    Решение: Время: $2,5$ ч. Общая скорость: $55 + 65 = 120$ см/ч. Длина: $120 \cdot 2,5 = 300$ см = $3$ м.
    Ответ: $3 \mathrm{M}$.
13. Петя ходит в бассейн один раз в 2 дня, Коля – один раз в 4 дня, а Вова – один раз в 5 дней. Они встретились в бассейне во вторник. В какой день недели они встретятся вновь?
    Решение: НОК(2, 4, 5) = 20 дней. Через 20 дней от вторника: 20 mod 7 = 6 дней → понедельник.
    Ответ: в понедельник.
14. *На какую цифру оканчивается сумма $9 \cdot 19 \cdot 29 \cdot \ldots \cdot 20129+1 ?$
    Решение: Все множители оканчиваются на 9. Произведение нечетного количества таких чисел оканчивается на 9. Прибавив 1, получим 0.
    Ответ: на 0.
15. *Сколько существует пятизначных чисел, у которых третья цифра 7, а последняя цифра четная?
    Решение: Первая цифра: 9 вариантов (1-9), вторая: 10 (0-9), третья: 1 (7), четвертая: 10 (0-9), пятая: 5 (0,2,4,6,8). Всего: $9 \cdot 10 \cdot 10 \cdot 5 = 4500$.
    Ответ: 4500.