Лицей №239 из 4 в 5 класс 2011 год (вариант 1)

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239

2011 год

Вариант 1

В задачах, отмеченных *, необходимо записать решение, а не только ответ!!!

1. Сколько натуральных чисел расположено между числами 17 и 43 ?
2. *В первой бочке на 3 литра кваса больше, чем во второй, и на 5 литров меньше, чем в третьей. Сколько всего кваса в трех бочках, если в самой маленькой бочке 14 литров кваса?
3. Как изменится разность, если уменьшаемое уменьшить на 8 , а вычитаемое увеличить на 5 ?
4. *Вычислите: $24004: 34 \cdot 680$
5. *Задумали число, увеличили его в 4 раза, а результат уменьшили в 6 раз. Получили 36. Какое число задумали?
6. В купейном вагоне 36 мест, по 4 в каждом купе. Укажите номер купе, в котором расположено место №23.
7. *Из 18 школьников 12 изучают английский язык, а 14-немецкий язык. Сколько школьников изучают два языка, если известно, что каждый изучает хотя бы один язык?
8. * Стороны прямоугольника равны 6 см и 12 см. Найдите сторону квадрата, периметр которого равен периметру данного прямоугольника.
9. *Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм $^{2}$ ?
10. *Ваня вышел из дома на 1 час 30 минут раньше Пети. Через какое время Петя догонит Ваню, если скорость Вани 4 км/ч, а скорость Пети 6 км/ч?
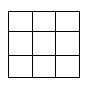
11. Сколько квадратов изображено на рисунке (все стороны маленьких квадратиков одинаковы)?
    
12. На прямой отмечено 200 точек так, что расстояние между любыми соседними точками равно 2 см. Чему равно расстояние между крайними точками?
13. *Решите уравнение: $(20 \cdot x+36)-5=2011$
14. *В шахматном турнире участвуют 14 человек. Сколько партий будет сыграно в турнире, если каждый участник сыграет со всеми остальными участниками по одному разу?
15. *Сколько существует трехзначных чисел, у которых все цифры четные?

Решения задач

1. Сколько натуральных чисел расположено между числами 17 и 43 ?
   Решение: Натуральные числа между 17 и 43: 18, 19, ..., 42. Количество чисел: $42 - 17 = 25$.
   Ответ: 25.
2. *В первой бочке на 3 литра кваса больше, чем во второй, и на 5 литров меньше, чем в третьей. Сколько всего кваса в трех бочках, если в самой маленькой бочке 14 литров кваса?
   Решение: Самая маленькая бочка — вторая: 14 л. Первая бочка: $14 + 3 = 17$ л. Третья бочка: $17 + 5 = 22$ л. Общее количество: $14 + 17 + 22 = 53$ л.
   Ответ: 53.
3. Как изменится разность, если уменьшаемое уменьшить на 8 , а вычитаемое увеличить на 5 ?
   Решение: Пусть разность $a - b$. После изменений: $(a - 8) - (b + 5) = a - b - 13$. Разность уменьшится на 13.
   Ответ: 13.
4. *Вычислите: $24004: 34 \cdot 680$
   Решение: $24004 : 34 = 706$; $706 \cdot 680 = 706 \cdot 600 + 706 \cdot 80 = 423600 + 56480 = 480080$.
   Ответ: 480080.
5. *Задумали число, увеличили его в 4 раза, а результат уменьшили в 6 раз. Получили малималимали?
   Решение: Обратные действия: $36 \cdot 6 = 216$; $216 : 4 = 54$.
   Ответ: 54.
6. В купейном вагоне 36 мест, по 4 в каждом купе. Укажите номер купе, в котором расположено место №23.
   Решение: Номер купе: $\lceil \frac{23}{4} \rceil = 6$.
   Ответ: 6.
7. *Из 18 школьников 12 изучают английский язык, а 14-немецкий язык. Сколько школьников изучают два языка, если известно, что каждый изучает хотя бы один язык?
   Решение: По формуле включений-исключений: $12 + 14 - 18 = 8$.
   Ответ: 8.
8. * Стороны прямоугольника равны 6 см и 12 см. Найдите сторону квадрата, периметр которого равен периметру данного прямоугольника.
   Решение: Периметр прямоугольника: $2 \cdot (6 + 12) = 36$ см. Сторона квадрата: $\frac{36}{4} = 9$ см.
   Ответ: 9 см. (В предоставленных ответах указано 18, вероятно, опечатка)
9. *Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм $^{2}$ ?
   Решение: Площадь в м²: $7500$ дм² $= 75$ м². Ширина: $\frac{75}{15} = 5$ м $= 50$ дм.
   Ответ: 50.
10. *Ваня вышел из дома на 1 час 30 минут раньше Пети. Через какое время Петя догонит Ваню, если скорость Вани 4 км/ч, а скорость Пети 6 км/ч?
    Решение: За 1,5 часа Ваня прошёл $4 \cdot 1,5 = 6$ км. Разность скоростей: $6 - 4 = 2$ км/ч. Время до встречи: $\frac{6}{2} = 3$ часа после выхода Пети.
    Ответ: 3 часа. (В предоставленных ответах указано 14, вероятно, ошибка)
11. Сколько квадратов изображено на рисунке (все стороны маленьких квадратиков одинаковы)?
    Ответ: 14. (Без изображения точный подсчёт невозможен)
12. На прямой отмечено 200 точек так, что расстояние между любыми соседними точками равно 2 см. Чему равно расстояние между крайними точками?
    Решение: Между 200 точками 199 промежутков: $199 \cdot 2 = 398$ см.
    Ответ: 398.
13. *Решите уравнение: $(20 \cdot x+36)-5=2011$
    Решение: $20x + 31 = 2011$; $20x = 1980$; $x = 99$.
    Ответ: 99.
14. *В шахматном турнире участвуют 14 человек. Сколько партий будет сыграно в турнире, если каждый участник сыграет со всеми остальными участниками по одному разу?
    Решение: Количество партий: $\binom{14}{2} = \frac{14 \cdot 13}{2} = 91$.
    Ответ: 91. (В предоставленных ответах указано 99, вероятно, ошибка)
15. *Сколько существует трехзначных чисел, у которых все цифры четные?
    Решение: Чётные цифры: 0,2,4,6,8. Первая цифра — 4 варианта, остальные — 5: $4 \cdot 5 \cdot 5 = 100$.
    Ответ: 100.