8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 4 в 5 класс 2010 год (вариант 1)

Сложность:
Дата экзамена: 2010
Сложность:
Дата экзамена: 2010
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239


2010 год


Вариант 1




В задачах, отмеченных *, должны быть написаны полные решения!

  1. Запишите цифрами число: двести тысяч триста девять.
  2. Назовем число хорошим, если его можно получить, перемножая только двойки и тройки. Перечислите все хорошие числа от 4 до 20 .
  3. *Найдите неизвестное значение $x$ из равенства: $((2010-x): 3+31): 25+211=239$
  4. *Бревно нужно распилить на 6 частей. За сколько времени это можно сделать, если один распил занимает 1 мин 30 сек? 5. Как 55 грибов разложить на 9 тарелок так, чтобы в каждой тарелке было разное количество грибов?
  5. * Площадь прямоугольника равна 30 кв. см, а одна из его сторон равна 10 см. Чему равен периметр этого прямоугольника?
  6. Дядя Фёдор, кот Матроскин, Шарик и почтальон Печкин сидят на скамейке. Если Шарик, сидящий справа от всех, сядет между дядей Фёдором и котом, то кот будет крайним слева. В каком порядке они сидят?
  7. *Доктор Айболит раздал четырём заболевшим зверям 2010 чудодейственных таблеток. Носорог получил на одну больше, чем крокодил, бегемот на одну больше, чем носорог, а слон на одну больше, чем бегемот. Сколько таблеток придётся съесть слону?
  8. *Вычислите: $281 \cdot 323+281 \cdot 227+119 \cdot 550$.
  9. *Какое число надо умножить на 10, чтобы результат был таким же, как при прибавлении к этому числу $18 ?$
  10. Квадрат сложен из четырех одинаковых квадратов периметром 14 м каждый. Чему равен периметр большого квадрата?
  11. Представьте число 405 в виде произведения нескольких чисел, сумма которых равна $20 .$
  12. *На ферме имеются гуси и коровы общим числом 30, а общее количество ног у них равно $86 .$ Сколько на ферме гусей?
  13. Поезд проехал расстояние 168 км между двумя пунктами за 6 часов. За какое время проедет это расстояние мотоцикл, скорость которого в 3 раза больше?
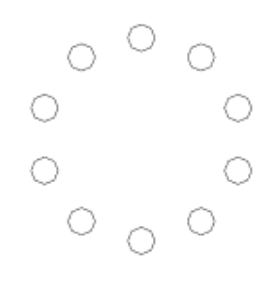
  14. Расположите в кружочках числа от 1 до 10 так (прямо на рисунке слева), чтобы для любых двух соседних чисел их сумма была равна сумме двух чисел, им противоположных (симметричных относительно центра окружности).
  15. Имеются два кувшина: один объемом 5 л, а второй объемом 3 или 4 литра. На взгляд нельзя определить объем кувшина или воды в нем. Опишите, как определить объем второго кувшина, находясь возле реки?
Материалы школы Юайти
youit.school ©
Ответы:


  1. 200309
  2. 4; 6; 8; 9; 12; 16; 18
  3. 3
  4. 7:30
  5. 2+3+4+5+6+7+8+9+11
  6. 26
  7. МФПШ
  8. 504
  9. 220000
  10. 2
  11. 28
  12. 5*9*3*3
  13. 17
  14. 2
  15. 5; 8; 2; 9; 1; 10; 3; 7; 4; 6
Материалы школы Юайти
youit.school ©

Решения задач



  1. Запишите цифрами число: двести тысяч триста девять.
    Решение: Двести тысяч = 200 000, триста девять = 309. Объединяем: 200000 + 309 = 200309.
    Ответ: 200309.
  2. Назовем число хорошим, если его можно получить, перемножая только двойки и тройки. Перечислите все хорошие числа от 4 до 20.
    Решение: Перемножая двойки и тройки, получаем:
    $4 = 2 \cdot 2$, $6 = 2 \cdot 3$, $8 = 2 \cdot 2 \cdot 2$, $9 = 3 \cdot 3$, $12 = 2 \cdot 2 \cdot 3$, $16 = 2 \cdot 2 \cdot 2 \cdot 2$, $18 = 2 \cdot 3 \cdot 3$.
    Ответ: 4; 6; 8; 9; 12; 16; 18.
  3. Найдите неизвестное значение $x$ из равенства: $((2010 - x) : 3 + 31) : 25 + 211 = 239$.
    Решение:
    $((2010 - x) : 3 + 31) : 25 = 239 - 211 = 28$
    $(2010 - x) : 3 + 31 = 28 \cdot 25 = 700$
    $(2010 - x) : 3 = 700 - 31 = 669$
    $2010 - x = 669 \cdot 3 = 2007$
    $x = 2010 - 2007 = 3$
    Ответ: 3.
  4. Бревно нужно распилить на 6 частей. За сколько времени это можно сделать, если один распил занимает 1 мин 30 сек?
    Решение: Для получения 6 частей требуется 5 распилов. Время: $5 \cdot 1{,}5$ мин = 7 мин 30 сек.
    Ответ: 7 мин 30 сек.
  5. Как 55 грибов разложить на 9 тарелок так, чтобы в каждой тарелке было разное количество грибов?
    Решение: Минимальная сумма чисел от 1 до 9: $1 + 2 + \ldots + 9 = 45$. Необходимо добавить 10 грибов. Увеличиваем наибольшее число: $1, 2, 3, 4, 5, 6, 7, 8, 19$ (сумма 55).
    Ответ: 1, 2, 3, 4, 5, 6, 7, 8, 19.
  6. Площадь прямоугольника равна 30 кв. см, а одна из его сторон равна 10 см. Чему равен периметр этого прямоугольника?
    Решение: Вторая сторона: $30 : 10 = 3$ см. Периметр: $2 \cdot (10 + 3) = 26$ см.
    Ответ: 26 см.
  7. Дядя Фёдор, кот Матроскин, Шарик и почтальон Печкин сидят на скамейке. Если Шарик, сидящий справа от всех, сядет между дядей Фёдором и котом, то кот будет крайним слева. В каком порядке они сидят?
    Решение: Исходный порядок: Матроскин (кот), Дядя Фёдор, Печкин, Шарик. После перемещения Шарика между Дядей и котом порядок: Шарик, Матроскин, Дядя Фёдор, Печкин. Кот становится крайним слева.
    Ответ: Матроскин, Дядя Фёдор, Печкин, Шарик.
  8. Доктор Айболит раздал четырём заболевшим зверям 2010 чудодейственных таблеток. Носорог получил на одну больше, чем крокодил, бегемот на одну больше, чем носорог, а слон на одну больше, чем бегемот. Сколько таблеток придётся съесть слону?
    Решение: Пусть крокодил получил $x$ таблеток. Тогда:
    $x + (x + 1) + (x + 2) + (x + 3) = 2010$
    $4x + 6 = 2010$
    $4x = 2004$
    $x = 501$
    Слон получил: $501 + 3 = 504$ таблетки.
    Ответ: 504.
  9. Вычислите: $281 \cdot 323 + 281 \cdot 227 + 119 \cdot 550$.
    Решение:
    $281 \cdot (323 + 227) + 119 \cdot 550 = 281 \cdot 550 + 119 \cdot 550 = 550 \cdot (281 + 119) = 550 \cdot 400 = 220000$.
    Ответ: 220000.
  10. Какое число надо умножить на 10, чтобы результат был таким же, как при прибавлении к этому числу 18?
    Решение: Уравнение: $10x = x + 18$
    $9x = 18$
    $x = 2$
    Ответ: 2.
  11. Квадрат сложен из четырех одинаковых квадратов периметром 14 м каждый. Чему равен периметр большого квадрата?
    Решение: Сторона малого квадрата: $14 : 4 = 3{,}5$ м. Сторона большого квадрата: $3{,}5 \cdot 2 = 7$ м. Периметр: $4 \cdot 7 = 28$ м.
    Ответ: 28 м.
  12. Представьте число 405 в виде произведения нескольких чисел, сумма которых равна 20.
    Решение: $405 = 5 \cdot 9 \cdot 3 \cdot 3$. Сумма: $5 + 9 + 3 + 3 = 20$.
    Ответ: $5 \cdot 9 \cdot 3 \cdot 3$.
  13. На ферме имеются гуси и коровы общим числом 30, а общее количество ног у них равно 86. Сколько на ферме гусей?
    Решение: Пусть гусей $x$, коров $30 - x$. Уравнение:
    $2x + 4(30 - x) = 86$
    $2x + 120 - 4x = 86$
    $-2x = -34$
    $x = 17$
    Ответ: 17.
  14. Поезд проехал расстояние 168 км между двумя пунктами за 6 часов. За какое время проедет это расстояние мотоцикл, скорость которого в 3 раза больше?
    Решение: Скорость поезда: $168 : 6 = 28$ км/ч. Скорость мотоцикла: $28 \cdot 3 = 84$ км/ч. Время: $168 : 84 = 2$ часа.
    Ответ: 2 часа.
  15. Расположите в кружочках числа от 1 до 10 так, чтобы для любых двух соседних чисел их сумма была равна сумме двух чисел, им противоположных.
    Решение: Противоположные пары: (1,10), (2,9), (3,8), (4,7), (5,6). Расположение: 5, 8, 2, 9, 1, 10, 3, 7, 4, 6.
    Ответ: 5, 8, 2, 9, 1, 10, 3, 7, 4, 6.
  16. Имеются два кувшина: один объемом 5 л, а второй объемом 3 или 4 литра. Как определить объем второго кувшина?
    Решение: Наполнить 5-литровый кувшин, перелить воду во второй. Если осталось 2 л, то второй кувшин 3 л. Если осталось 1 л, то второй кувшин 4 л.
    Ответ: Измерить остаток после переливания.
Материалы школы Юайти