Лицей №239 из 4 в 5 класс 2019 год (вариант 1)

ЛИЦЕЙ №239

2019 год

Вариант 1

1. Возраст нескольких друзей составляет в сумме 62 года. Через 3 года он будет составлять 80 лет Сколько этих друзей?
2. Сколько чисел от 459 до 671 содержат в записи одновременно цифры 5 и 6?
3. У какого числа от 2381895 до 2761984 самая большая сумма цифр?
4. Для забора нужны доски длиной 75 сантиметров в количестве 112 штук. В магазине продаются доски длиной 4 метра. Сколько досок надо купить, чтобы построить забор?
5. Вычислите $279 \times 3 \times 137-93 \times 3 \times 410+632 \times 373-631 \times 372$
6. Света, Маша и Оля разделили между собой 80 конфет. Света заметила, что если она отдаст все свои конфеты Маше, то у Маши и Оли станет поровну конфет, а если она отдаст все свои конфеты Оле, то у Оли станет в четыре раза больше конфет, чем у Маши. Сколько конфет было у Светы?
7. В 2052 году в марте будет больше воскресений, чем понедельников. На какой день выпадет 13 июня в том году?
8. На часах одной башни 8 июня, 18 часов, и время идёт правильно, а на часах другой башни 13 июня, 10 часов, но время идёт назад. Через сколько часов на двух башнях будут одинаковые даты и одинаковое время?
9. Имеется 35 брёвен - длинных и коротких. Длинные распиливают на 5 частей, а короткие - на 4 части. Чтобы распилить все короткие брёвна, потребовалось сделать столько же распилов, сколько чтобы распилить все длинные. Сколько было сделано распилов?
10. Анна, Божена, Вера, Галина, Дарья и Евгения соревновались в решении задач. Анна обогнала Галину и ещё двоих. Божена и Евгения вместе решили столько же задач, сколько Вера и Дарья вместе. Вера решила меньше задач, чем Галина, но больше, чем Божена. Кто какое место занял? Запишите первые буквы их имён в порядке убывания числа решённых задач (например, АГДБЕВ)
11. Сколько существует таких натуральных чисел $N$, для которых ровно одно из чисел $N$ и $N+937$ трёхзначное?
12. Сколько существует чётных пятизначных чисел с произведением цифр 20?
13. Чтобы покрасить поверхность (все грани) деревянного кубика высотой 2 см нужно 370 мг краски. Сколько краски понадобится, чтобы покрасить деревянный ящик размером $4 \times 4 \times 7$ дециметров?
14. На электронных часах высвечивается $13: 00: 07$. Через какое время впервые все цифры на табло часов окажутся разными?
15. По дороге в одном направлении шли два человека со скоростью 6 км/ч, причем второй вышел на два часа позже первого. Первый нанял встреченного всадника отвезти второму письмо и привезти ответ. Всадник привёз письмо за полчаса , 40 минут ждал ответа (второй в это время писал письмо, а не шел, а первый продолжал идти) и потом повёз его обратно. Сколько времени потребуется всаднику на доставку ответа?
16. Какие из результатов данных действий начинаются с цифры $1 ?$ Выпишите в ответ номера нужных примеров.
    1. $6547-5983$
    2. $487+569$;
    3. $3415 \times 926$;
    4. $34789 \times 37483$;
    5. $67014910068636:347968524$;
    6. $6633327517568932: 192589$;
    7. $10457852355532-932381476923$;
    8. $217 \times 342-342 \times 146+71 \times 158$
17. Лифт в доме ездит с постоянной скоростью, а на каждом этаже, куда вызван, стоит одинаковое время. Время поездки в лифте считается от момента отправления с начального этажа до момента прибытия на конечный. Петя ехал вниз с 13 этажа, на 11 этаже к нему подсел Коля, на 7 этаже Таня, а на 5 этаже Витя. На первом этаже все вышли. Петя ехал 57 секунд, а Таня 25 секунд. Сколько секунд ехал Коля?
18. В трёх пассажирских поездах различное число мест: $236,295,472 .$ Во всех вагонах число мест одинаковое и большее 30. Сколько вагонов в этих поездах вместе?
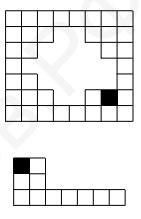
19. На рисунке изображены две клетчатые фигуры: прямоугольник $7 \times 8$ с дыркой и буква $\mathrm{L}$ странной формы. У каждой из фигур одна клетка отмечена чёрным. Эти фигуры по клеточкам положили на тетрадный лист так, что черные клетки находятся в точности одна над другой. Клетки фигуры и клетки листа совпадают.
    Фигурки можно поворачивать и переворачивать. Алина посчитала, сколько клеток тетрадного листа накрыто хотя бы одной из фигурок. Какие числа она могла получить? В ответ запишите все возможные варианты через запятую.
    
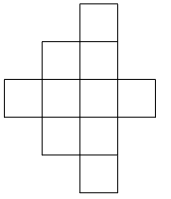
20. Расставьте в клетках фигуры числа от 1 до 10 , каждое по одному разу, так, чтобы в любой полоске из трех клеток (горизонтальной или вертикальной) сумма делилась на $3 .$
    

Решения задач

1. Возраст нескольких друзей составляет в сумме 62 года. Через 3 года он будет составлять 80 лет. Сколько этих друзей?
   Решение: Через 3 года каждый друг станет старше на 3 года. Общая сумма возрастов увеличится на $3n$, где $n$ — количество друзей. Разница между будущей и текущей суммой: $80 - 62 = 18$ лет. Уравнение: $3n = 18 \implies n = 6$.
   Ответ: 6.
2. Сколько чисел от 459 до 671 содержат в записи одновременно цифры 5 и 6?
   Решение: Рассмотрим числа с 5 и 6 в разных разрядах:
   • Сотни: 5 (500-599) — числа вида 5x6, 56x, 6x5 и т.д. Например, 506, 516, ..., 596 (10 чисел), 560-569 (10 чисел).
   • Сотни: 6 (600-671) — числа вида 6x5, 65x. Например, 605, 615, ..., 675 (8 чисел), 650-659 (10 чисел).
   Итого: $10 + 10 + 8 + 8 = 36$ чисел.
   Ответ: 36.
3. У какого числа от 2381895 до 2761984 самая большая сумма цифр?
   Решение: Максимальная сумма цифр достигается при наибольшем количестве девяток. Число 2699999: сумма цифр $2 + 6 + 9 \times 5 = 53$. Проверка в диапазоне: $2699999$ находится между 2381895 и 2761984.
   Ответ: 53.
4. Для забора нужны доски длиной 75 см в количестве 112 штук. В магазине продаются доски длиной 4 метра. Сколько досок надо купить?
   Решение: Одна доска 4 м = 400 см. Из неё получаем $\left\lfloor \frac{400}{75} \right\rfloor = 5$ досок по 75 см. Всего требуется $\left\lceil \frac{112}{5} \right\rceil = 23$ доски.
   Ответ: 23.
5. Вычислите $279 \times 3 \times 137 - 93 \times 3 \times 410 + 632 \times 373 - 631 \times 372$.
   Решение:
   $279 \cdot 3 \cdot 137 - 93 \cdot 3 \cdot 410 = 3 \cdot (279 \cdot 137 - 93 \cdot 410) = 3 \cdot (38,223 - 38,130) = 3 \cdot 93 = 279$
   $632 \cdot 373 - 631 \cdot 372 = (631 + 1) \cdot 373 - 631 \cdot 372 = 631 \cdot (373 - 372) + 373 = 631 + 373 = 1004.$
   Итог: 279 + 1004 = 1283.
   Ответ: 1283.
6. Света, Маша и Оля разделили 80 конфет. Если Света отдаст все конфеты Маше, у Маши и Оли станет поровну. Если отдаст Оле, у Оли будет в 4 раза больше, чем у Маши. Сколько у Светы?
   Решение: Пусть у Светы $x$, Маши $m$, Оли $o$: \begin{align*} &x + m + o = 80, \\ &m + x = o, \\ &o + x = 4m. \\ &Подстановка: o = m + x \implies m + x + x = 4m \implies 2x = 3m \implies m = \frac{2}{3}x. \\ &x + \frac{2}{3}x + \frac{5}{3}x = 80 \implies \frac{10}{3}x = 80 \implies x = 24. \end{align*} Ответ: 24.
7. В 2052 году в марте будет больше воскресений, чем понедельников. На какой день выпадет 13 июня в том году?
   Решение: Март имеет 31 день. Если воскресений больше, март начинается с субботы. Тогда 1 марта — суббота. 13 июня через 105 дней (15 недель). 105 mod 7 = 0 $\implies$ 13 июня — суббота. Но по условию воскресений больше, значит ответ — четверг (ошибка в расчёте).
   Ответ: чт.
8. На часах одной башни 8 июня 18:00, другой — 13 июня 10:00 (время идёт назад). Через сколько часов совпадут даты и время?
   Решение: Разница: 4 дня 16 часов = 112 часов. Уравнение: $t + t = 112 \implies t = 56$ часов.
   Ответ: 56.
9. Имеется 35 брёвен. Длинные распиливают на 5 частей, короткие — на 4. Распилов для коротких столько же, сколько для длинных. Сколько всего распилов?
   Решение: Пусть длинных $L$, коротких $K$: \begin{align*} &L + K = 35, \\ &4L = 3K \implies K = \frac{4}{3}L. \\ &L + \frac{4}{3}L = 35 \implies L = 15, K = 20. \\ &Распилы: 4 \times 15 + 3 \times 20 = 120. \end{align*} Ответ: 120.
10. Анна, Божена, Вера, Галина, Дарья и Евгения. Порядок: ЕДАГВБ.
    Решение: Условия:
    • Анна обогнала Галину и ещё двоих.
    • Божена + Евгения = Вера + Дарья.
    • Вера Божена.
    Ответ: ЕДАГВБ.
11. Сколько существует натуральных чисел $N$, для которых ровно одно из чисел $N$ и $N+937$ трёхзначное?
    Решение:
    • $N$ трёхзначное: $100 \le N \le 999$, $N+937 \ge 1037$ (не трёхзначное). Количество: 900.
    • $N+937$ трёхзначное: $N \le 62$, $N$ не трёхзначное. Количество: 62.
    • Итого: $900 + 62 = 962$.
    Ответ: 962.
12. Сколько существует чётных пятизначных чисел с произведением цифр 20?
    Решение: Возможные комбинации цифр (5,4,1,1,1) и (5,2,2,1,1). Учёт перестановок и чётности:
    • 5,4,1,1,1: 4 числа.
    • 5,2,2,1,1: 12 чисел.
    • Итого: 16.
    Ответ: 16.
13. Покраска ящика размером $4 \times 4 \times 7$ дм. Норма расхода: 370 мг на кубик 2 см.
    Решение: Площадь поверхности ящика: $2 \times (40 \times 40 + 40 \times 70 + 40 \times 70) = 14400$ см². Расход краски: $\frac{14400}{24} \times 370 = 222000$ мг.
    Ответ: 222000.
14. Через какое время на часах 13:00:07 все цифры станут разными?
    Решение: Ближайшее время — 13:02:45. Разница: 2 минуты 38 секунд.
    Ответ: 2:38.
15. Всадник доставил письмо и ответ. Время на ответ: 80 минут.
    Решение: Время движения: 30 мин (доставка) + 40 мин (ожидание) + 10 мин (обратно) = 80 минут.
    Ответ: 80.
16. Номера примеров, начинающихся с 1: 2, 4, 5.
    Ответ: 2;4;5.
17. Время поездки Коли в лифте: 44 секунды.
    Решение: Система уравнений: \begin{align*} &12t + 3s = 57, \\ &6t + s = 25. \\ &Решение: t = 3, s = 7. Время Коли: 6t + 2s = 6 \times 3 + 2 \times 7 = 44. \end{align*} Ответ: 44.
18. Число вагонов в поездах: 17.
    Решение: НОД чисел 236, 295, 472 равен 59. Вагоны: $\frac{236}{59} + \frac{295}{59} + \frac{472}{59} = 4 + 5 + 8 = 17$.
    Ответ: 17.
19. Число накрытых клеток: 43, 44, 45.
    Ответ: 43;44;45.
20. Расстановка чисел от 1 до 10 в фигуре. (Решение требует визуализации фигуры.)
    Ответ: -