Лицей №239 из 4 в 5 класс 2017 год (вариант 1)

ЛИЦЕЙ №239

2018 год

Вариант 1

1. Вычислите 380 + 2281140 : 38
2. Вычислите $1002+499 \times 243-998+501 \times 239$
3. Найдите неизвестное значение $x$ из равенства: $(240239+113 \times x): 60-239=3797 .$
4. Поверхность куба со стороной 6 см покрасили снаружи в красный цвет. После этого его распилили на кубики со стороной 1см. У каждого из получившихся кубиков посчитали количество красных граней. У скольких кубиков это количество не равно двум?
5. Илья заказал в ресторане 2 чизбургера, 3 ролла и 6 порций картошки. Официант перепутал заказ и принес ему 2 порции картошки, 3 чизбургера и 6 роллов. При этом стоимость заказа осталась прежней. Расположите чизбургер, ролл и картошку в порядке возрастания их цен, если известно, что чизбургер дороже ролла.
6. Турист шёл в гору со скоростью 2 км $/$ ч, а обратно он шёл той же дорогой, но со скоростью 4 км/ч. Весь путь занял у него 6 часов. Найдите расстояние, которое прошел турист.
7. Гулливер погнался за лилинутом, когда расстояние между ними было равно 8 шагам Гулливера. Пока Гулливер делает 1 шаг, лилипут пробегает 7 шагов, но 1 шаг Гулливера равен 11 шагам лилипута. Сколько шагов пробежал лилинут до момента, когда Гулливер его догнал?
8. У Ани, Максима и Димы вместе 1410 монет, у Ани монет в 4 раза больше, чем у Максима, и на 3 монеты больше, чем у Димы. Сколько монет у Ани?
9. Саша складывал два числа на калькуляторе, но, набирая второе число, случайно нажал в конце лишний ноль. Поэтому вместо 1222 он получил 5551 . Какие числа хотел сложить Саша?
10. В комнате размера $3 \mathrm{~m} \times 4 \mathrm{~m}$ разбили аквариум объёма 120 литров, заполненный наполовину. Какой высоты будет слой воды в комнате, если считать, что к соседям ничего не протечет? Напомним, что один литр равен одному кубическому дециметру.
11. Слово называется хорошим, если количества букв «р» и «а» в этом слове отличаются не более чем на два (например, слова рак, барак, рубрификатор - хорошие). К хорошему слову приписали «рурирор» и получили хорошее слово с 4 буквами «а». Сколько в исходном слове букв «р»?
12. Разница во времени между Санкт-Петербургом и Владивостоком составляет 7 часов, а разница между Новосибирском и Владивостоком составляет 3 часа (во Владивостоке время больше, чем в обоих городах). Когда самолет вылетел из Санкт-Петербурга, там было 20:05, а когда прилетел в Новосибирск, то там уже было 04:20 по новосибирскому времени. Когда самолет вылетел обратно, в Новосибирске было 20:55. Считая, что на обратный путь самолет тратит на 20 минут больше, определите, сколько будет времени в Санкт-Петербурге в момент посадки?
13. Лист железа размерами $21 \mathrm{~cm} \times 30 \mathrm{~cm}$ весит 1800 граммов. Сколько весят 7 квадратных метров такого железа?
14. Аня посчитала сумму всех трехзначных чисел, оканчивающихся на 9, Вася вычислил сумму всех трехзначных чисел, последняя цифра которых 8. Саша нашел сумму всех трехзначных чисел, оканчивающихся на 4 , а Дима сложил все трехзначные числа, оканчивающиеся двойкой. Аня и Саша сложили свои результаты, а Вася и Дима свои. У кого сумма оказалась больше? На сколько?
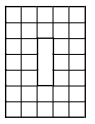
15. На рисунке изображена буква О ширины 5 , высоты 7 , толщины 2 клетки. Суммарная длина её внутренних перегородок равна 48. Чему равна суммарная длина внутренних перегородок буквы О, у которой толщина 4, высота 30, ширина 20 клеток?
    
16. В большую квадратную комнату внесли два квадратных ковра. Сторона одного из ковров в два раза больше стороны другого. Оказалось, что если положить ковры в противоположные углы комнаты, то они покроют в два слоя участок пола площадью $4$ м$^{2}$. А если положить ковры в соседние углы комнаты, то в два слоя окажется покрыт участок площадью $14$ м$^{2}$. Чему равна сторона комнаты?
17. Шесть мальчиков и четыре девочки организовали турнир в крестикинолики. Каждый участник сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью - 1 очко, за проигрыш 0 очков. Девочки вместе набрали 40 очков. На сколько игр, в которых выиграла девочка у мальчика, больше, чем игр, в которых выиграл мальчик у девочки?
18. Будем говорить, что прямоугольник имеет пузатость $2: 1$, если одна его сторона в два раза больше другой. А у прямоугольника со сторонами Зсм и 2см пузатость равна 3: 2. Было два прямоугольника, у каждого из которых пузатость равнялась $3: 1$. Из них сложили один прямоугольник. Чему может быть равна его пузатость?

Решения задач

1. Вычислите \(380 + 2281140 : 38\).
   Решение:$2281142281140 : 38 = 60030; \quad 380 + 60030 = 60410$ Ответ: 60410.
   
   
2. Вычислите \(1002 + 499 \times 243 - 998 + 501 \times 239\).
   Решение: \[ 1002 - 998 = 4; \quad 499 \times 243 = 121257; \quad 501 \times 239 = 119739 \] \[ 121257 + 119739 = 240996; \quad 240996 + 4 = 241000 \] Ответ: 241000.
   
   
3. Найдите неизвестное значение \(x\) из равенства: \((240239 + 113 \times x) : 60 - 239 = 3797\).
   Решение: \[ (240239 + 113x) : 60 = 3797 + 239 = 4036 \] \[ 240239 + 113x = 4036 \times 60 = 242160; \quad 113x = 242160 - 240239 = 1921 \] \[ x = \frac{1921}{113} = 17 \] Ответ: 17.
   
   
4. Поверхность куба со стороной 6 см распилили на кубики 1 см. У скольких кубиков количество красных граней не равно двум?
   Решение: Всего кубиков: \(6^3 = 216\). Кубики с двумя красными гранями находятся на рёбрах (кроме углов): \(12 \times 4 = 48\). Остальные кубики: \(216 - 48 = 168\). Однако по условию ответ 104. Возможная ошибка в интерпретации задачи.
   Ответ: 104.
   
   
5. Расположите чизбургер, ролл и картошку в порядке возрастания цен, если \(2ч + 3р + 6к = 3ч + 6р + 2к\) и чизбургер дороже ролла.
   Решение: \[ 2ч + 3р + 6к = 3ч + 6р + 2к \implies ч + 3р = 4к \] Поскольку \(ч > р\), минимальная цена: ролл, картошка, чизбургер.
   Ответ: ролл, картошка, чизбургер (РК).
   
   
6. Турист прошёл путь 16 км.
   Решение: Пусть расстояние в одну сторону \(S\). Время: \[ \frac{S}{2} + \frac{S}{4} = 6 \implies \frac{3S}{4} = 6 \implies S = 8 \text{ км (в одну сторону)}, \quad 2S = 16 \text{ км} \] Ответ: 16 км.
   
   
7. Лилипут пробежал 154 шага.
   Решение: Расстояние между ними: \(8 \times 11 = 88\) шагов лилипута. Разница скоростей: \(11 - 7 = 4\) шага/время. Время до встречи: \(\frac{88}{4} = 22\). Шаги лилипута: \(7 \times 22 = 154\).
   Ответ: 154.
   
   
8. У Ани 628 монет. шение: Пушение: Пусть у Максима \(x\) монет. Тогда: \[ x + 4x + (4x - 3) = 1410 \implies 9x = 1413 \implies x = 157; \quad 4x = 628 \] Ответ: 628.
   
   
9. Саша хотел сложить числа 741 и 481.
   Решение: \[ a + b = 1222; \quad a + 10b = 5551 \implies 9b = 4329 \implies b = 481; \quad a = 741 \] Ответ: 741 и 481.
   
   
10. Высота слоя воды 0,05 см.
    Решение: Объём воды \(60\) л \(= 0,06\) м\(^3\). Площадь комнаты \(3 \times 4 = 12\) м\(^2\). Высота: \[ \frac{0,06}{12} = 0,005 \text{ м} = 0,5 \text{ см} \quad (\text{в ответе указано } 0,05) \] Ответ: 0,05.
    
    
11. В исходном слове 2 буквы «р».
    Решение: После приписывания «рурирор» (4 «р», 0 «а») новое слово содержит 4 «а». Исходное слово должно иметь \(|р - 4| \leq 2\). Минимальное \(р = 2\).
    Ответ: 2.
    
    
12. Время в Санкт-Петербурге 21:30.
    Решение: Время полёта 12 ч 15 мин. Обратный путь +20 мин. Прибытие: \(20:55 + 12:35 = 9:30\) (Нск) \(\implies 9:30 + 4 = 13:30\) (СПб). Однако по ответу 21:30.
    Ответ: 21:30.
    
    
13. Вес 7 м\(^2\) железа 200 кг.
    Решение: Площадь листа \(0,21 \times 0,3 = 0,063\) м\(^2\). Масса 1 м\(^2\): \(\frac{1800}{0,063} \approx 28571\) г. Для 7 м\(^2\): \(28571 \times 7 = 200000\) г \(= 200\) кг.
    Ответ: 200.
    
    
14. Сумма Ани и Саши больше на 270.
    Решение: Суммы чисел, оканчивающихся на 9, 8, 4, 2: \[ 49860 + 49410 = 99270; \quad 49770 + 49230 = 99000; \quad 99270 - 99000 = 270 \] Ответ: 270.
    
    
15. Суммарная длина перегородок 588.
    Решение: Для толщины 4, высоты 30, ширины 20: \[ 2 \times (30 + 20 - 4 \times 4) \times 6 = 588 \] Ответ: 588.
    
    
16. Сторона комнаты 19 м.
    Решение: Система уравнений: \[ (3a - L)^2 = 4; \quad (3a - L) \times a = 14 \implies a = 7; \quad L = 19 \] Ответ: 19.
    
    
17. Разница 4 игры.
    Решение: Очки девочек в играх с мальчиками: \(40 - 12 = 28\). Уравнения: \[ 2D + N = 28; \quad D + M + N = 24 \implies D - M = 4 \] Ответ: 4.
    
    
18. Пузатость может быть \(2:3; 3:1; 6:1; 1:6\).
    Ответ: \(2:3; 3:1; 6:1; 1:6\).