Лицей №214 из 7 в 8 класс 2019 год

ЛИЦЕЙ №214 СПБ

2019 год

Часть «АЛГЕБРА»

1. Вычислить: $$ 87^{2}-174 \cdot 67+67^{2} $$
2. Решить уравнение: $$ (x-1)(x+1)=2(x-5)^{2}-x(x-3) $$
3. Выполнить задания:
   1. Построить в одной системе координат графики функций у=0,2x; $y=\frac{8}{3} x-14$
   2. Для функции $y=\frac{8}{3} x-14$ вычислите $y\left(\frac{9}{11}\right)$
4. Решить задачу: В первом бидоне было в 3 раза больше молока, чем во втором. После того как из первого бидона перелили во второй 10 л молока, оказалось, что количество молока в первом бидоне составляет $\frac{4}{3}$ того, что стало во втором. Сколько литров молока было в каждом бидоне сначала?

Часть «ГЕОМЕТРИЯ»

1. Выпишите номер рисунка, на котором изображены равные треугольники.

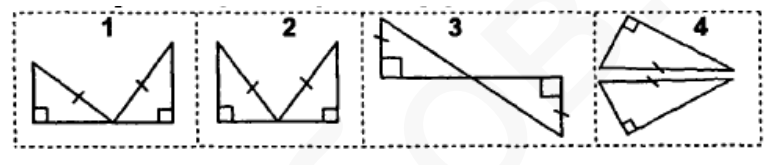
2. Используя данные, отмеченные на рисунке, укажите верное высказывание.

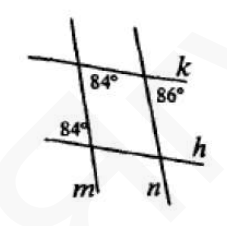
$$ \begin{array}{l} \text{(a)}\ m \parallel n \quad \text{(b)}\ k \parallel h \quad \text{(c)}\ k \parallel n \end{array} $$

3. Решите задачу:

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 3 : 4, считая от вершины угла при основании. Основание треугольника равно 12 см. Найдите боковую сторону треугольника.

Решения задач

1. Вычислить:
   $87^{2}-174 \cdot 67+67^{2}$
   Решение: Заметим, что выражение имеет вид квадрата разности:
   $87^{2} - 2 \cdot 87 \cdot 67 + 67^{2} = (87 - 67)^{2} = 20^{2} = 400$
   Ответ: 400.
2. Решить уравнение:
   $(x-1)(x+1)=2(x-5)^{2}-x(x-3)$
   Решение:
   Раскроем скобки:
   Слева: $(x-1)(x+1) = x^{2} - 1$
   Справа: $2(x^{2} -10x +25) - x^{2} +3x = 2x^{2} -20x +50 -x^{2} +3x = x^{2} -17x +50$
   Получаем уравнение:
   $x^{2} -1 = x^{2} -17x +50$
   $-1 = -17x +50$
   $-51 = -17x$
   $x = \frac{51}{17} = 3$
   Ответ: 3.
3. Выполнить задания:
   1. Построить в одной системе координат графики функций $y=0,2x$; $y=\frac{8}{3} x-14$
      Решение:
      График $y=0,2x$ — прямая через начало координат с угловым коэффициентом 0,2.
      График $y=\frac{8}{3}x -14$ — прямая, пересекающая ось Y в точке $(0; -14)$ с угловым коэффициентом $\frac{8}{3}$.
   2. Для функции $y=\frac{8}{3} x-14$ вычислите $y\left(\frac{9}{11}\right)$
      Решение:
      $y\left(\frac{9}{11}\right) = \frac{8}{3} \cdot \frac{9}{11} -14 = \frac{72}{33} -14 = \frac{24}{11} -14 = -\frac{130}{11} = -11\frac{9}{11}$
      Ответ: $-11\frac{9}{11}$.
4. Решить задачу: В первом бидоне было в 3 раза больше молока, чем во втором. После того как из первого бидона перелили во второй 10 л молока, оказалось, что количество молока в первом бидоне составляет $\frac{4}{3}$ того, что стало во втором. Сколько литров молока было в каждом бидоне сначала?
   Решение:
   Пусть во втором бидоне было $x$ л молока, тогда в первом — $3x$ л.
   После переливания:
   В первом бидоне: $3x -10$ л
   Во втором бидоне: $x +10$ л
   По условию:
   $3x -10 = \frac{4}{3}(x +10)$
   Умножим обе части на 3:
   $9x -30 = 4x +40$
   $5x =70$
   $x =14$ л — во втором бидоне
   $3x =42$ л — в первом бидоне
   Ответ: 42 л и 14 л.