Лицей №1580 из 7 в 8 класс 2015 год (вариант 6)

ЛИЦЕЙ №1580

2015 год

Вариант 6

1. Вычиолите: $\frac{\left(85 \frac{7}{30}-83 \frac{5}{18}\right): \frac{8}{9}}{0,2}$.
2. За первый месяц ученик решил $20 \%$ всех задач летнего задания, за 2 -й месяц - $25 \%$ оставшихся. После чего выяснилось, что за август ему предстоит решить еще 45 задач. Сколько задач в летнем задании?
3. Решите уравнение: $\frac{3 x+13}{7}-\frac{10-9 x}{14}=5-\frac{2-5 x}{2}$.
4. Решите уравнение: $x^{3}-5 x^{2}-9 x+45=0$.
5. Найдите значение выражения: $\frac{3^{30}-3 \cdot 9^{13}}{13 \cdot 27^{9}}$.
6. Разложите на множители: $a^{2}-25-10 c-c^{2}$.
7. Найдите коэффициент $b$ и постройте график функции $y=-1,5 x+b$, если известно, что он проходит через точку пересечения графика функции $y=3 x+3$ с осью ординат.
8. Поезд проходит расстояние от города $A$ до города $B$ за 10 ч 40 мин. Если бы скорость поезда была на 10 км/ч меньше, то он прибыл бы в $B$ на 2 ч 8 мин позже. Найдите расстояние между городами.
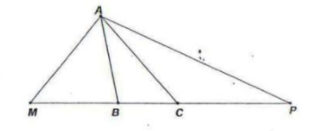
9. В треугольнике $A B C \angle B A C=30^{\circ}, A B=B M ; A C=C P$. Найдите $\angle M A P$.
10. Решите уравнение: $9 x^{2}-6 x+|3 x-5 y+1|=-1 .$
    

Решения задач

1. Вычислите: $\frac{\left(85 \frac{7}{30}-83 \frac{5}{18}\right): \frac{8}{9}}{0,2}$.
   Решение:
   Переведём смешанные числа в неправильные дроби:
   $85 \frac{7}{30} = \frac{85 \cdot 30 + 7}{30} = \frac{2557}{30}$; $83 \frac{5}{18} = \frac{83 \cdot 18 + 5}{18} = \frac{1499}{18}$
   Найдём разность: $\frac{2557}{30} - \frac{1499}{18} = \frac{2557 \cdot 3 - 1499 \cdot 5}{90} = \frac{7671 - 7495}{90} = \frac{176}{90} = \frac{88}{45}$
   Разделим на $\frac{8}{9}$: $\frac{88}{45} : \frac{8}{9} = \frac{88}{45} \cdot \frac{9}{8} = \frac{11}{5}$
   Разделим на 0,2: $\frac{11}{5} : 0,2 = \frac{11}{5} \cdot 5 = 11$
   Ответ: 11.
2. За первый месяц ученик решил $20 \%$ всех задач летнего задания, за 2-й месяц - $25 \%$ оставшихся. После чего выяснилось, что за август ему предстоит решить еще 45 задач. Сколько задач в летнем задании?
   Решение: Пусть всего задач $x$. После первого месяца осталось $0,8x$.
   Во второй месяц решили $0,25 \cdot 0,8x = 0,2x$. Остаток: $0,8x - 0,2x = 0,6x$.
   По условию: $0,6x = 45 \Rightarrow x = \frac{45}{0,6} = 75$
   Ответ: 75.
3. Решите уравнение: $\frac{3 x+13}{7}-\frac{10-9 x}{14}=5-\frac{2-5 x}{2}$.
   Решение: Умножим обе части на 14:
   $2(3x + 13) - (10 - 9x) = 70 - 7(2 - 5x)$
   Раскроем скобки: $6x + 26 - 10 + 9x = 70 - 14 + 35x$
   Упростим: $15x + 16 = 56 + 35x$
   Перенесём слагаемые: $-20x = 40 \Rightarrow x = -2$
   Ответ: $-2$.
4. Решите уравнение: $x^{3}-5 x^{2}-9 x+45=0$.
   Решение: Группируем слагаемые: $(x^3 - 5x^2) - (9x - 45) = x^2(x - 5) - 9(x - 5) = (x^2 - 9)(x - 5)$
   Разложим на множители: $(x - 3)(x + 3)(x - 5) = 0$
   Корни: $x = 3$, $x = -3$, $x = 5$
   Ответ: $-3$, $3$, $5$.
5. Найдите значение выражения: $\frac{3^{30}-3 \cdot 9^{13}}{13 \cdot 27^{9}}$.
   Решение: Представим степени с основанием 3:
   $9^{13} = 3^{26}$, $27^{9} = 3^{27}$
   Числитель: $3^{30} - 3 \cdot 3^{26} = 3^{26}(3^4 - 3) = 3^{26} \cdot 78$
   Знаменатель: $13 \cdot 3^{27} = 13 \cdot 3^{26} \cdot 3$
   Сокращаем: $\frac{78}{13 \cdot 3} = \frac{6}{3} = 2$
   Ответ: 2.
6. Разложите на множители: $a^{2}-25-10 c-c^{2}$.
   Решение: Группируем: $a^2 - (25 + 10c + c^2) = a^2 - (5 + c)^2 = (a - 5 - c)(a + 5 + c)$
   Ответ: $(a - c - 5)(a + c + 5)$.
7. Найдите коэффициент $b$ и постройте график функции $y=-1,5 x+b$, если известно, что он проходит через точку пересечения графика функции $y=3 x+3$ с осью ординат.
   Решение: Точка пересечения с осью ординат: $x = 0$, $y = 3 \cdot 0 + 3 = 3$ → $(0; 3)$
   Подставляем в уравнение: $3 = -1,5 \cdot 0 + b \Rightarrow b = 3$
   Уравнение: $y = -1,5x + 3$
   Ответ: $b = 3$.
8. Поезд проходит расстояние от города $A$ до города $B$ за 10 ч 40 мин. Если бы скорость поезда была на 10 км/ч меньше, то он прибыл бы в $B$ на 2 ч 8 мин позже. Найдите расстояние между городами.
   Решение: Пусть $S$ — расстояние, $v$ — исходная скорость.
   $10$ ч $40$ мин = $\frac{32}{3}$ ч; $2$ ч $8$ мин = $\frac{32}{15}$ ч
   Составим уравнения: $S = v \cdot \frac{32}{3}$ $S = (v - 10) \cdot \left(\frac{32}{3} + \frac{32}{15}\right) = (v - 10) \cdot \frac{192}{15}$
   Приравниваем: $v \cdot \frac{32}{3} = (v - 10) \cdot \frac{64}{5}$
   Упрощаем: $5v = 6(v - 10) \Rightarrow 5v = 6v - 60 \Rightarrow v = 60$ км/ч
   Расстояние: $S = 60 \cdot \frac{32}{3} = 640$ км
   Ответ: 640 км.
9. В треугольнике $ABC \angle BAC=30^{\circ}, AB=BM; AC=CP$. Найдите $\angle MAP$.
   Решение: Треугольники $ABM$ и $APC$ — равнобедренные.
   $\angle ABM = \angle AMB = \frac{180^\circ - 30^\circ}{2} = 75^\circ$
   $\angle APC = \angle ACP = \frac{180^\circ - 30^\circ}{2} = 75^\circ$
   $\angle MAP = 180^\circ - 75^\circ - 75^\circ = 30^\circ$
   Ответ: $30^\circ$.
10. Решите уравнение: $9 x^{2}-6 x+|3 x-5 y+1|=-1$.
    Решение: Преобразуем квадратичную часть: $9x^2 - 6x = (3x - 1)^2 - 1$
    Уравнение принимает вид: $(3x - 1)^2 - 1 + |3x - 5y + 1| = -1$
    Упрощаем: $(3x - 1)^2 + |3x - 5y + 1| = 0$
    Сумма неотрицательных слагаемых равна нулю только при: $\begin{cases} 3x - 1 = 0 \\ 3x - 5y + 1 = 0 \end{cases} \Rightarrow \begin{cases} x = \frac{1}{3} \\ 1 - 5y + 1 = 0 \Rightarrow y = \frac{2}{5} \end{cases}$
    Ответ: $\left(\frac{1}{3}; \frac{2}{5}\right)$.