Лицей №1580 из 7 в 8 класс 2015 год (вариант 5)

ЛИЦЕЙ №1580

2015 год

Вариант 5

1. Вычислитте: $\left(-6 \frac{7}{8}+1,375-5 \frac{1}{2} \cdot 0,73\right):(-1,73)$.
2. Сумма трех чисел равна 80. Первое число составляет $20 \%$ всей суммы, но $40 \%$ второго числа. Найдите среднее арифметическое первого и третьего чисел.
3. Решйте уравнение: $\frac{3+\cdot 2 x}{3}-\left(\frac{1+x}{5}-\frac{1-x}{6}\right)=1$.
4. Решите уравнение: $x^{3}-x^{2}-x+1=0$.
5. Найдите значение выражения: $\frac{\left(4 \cdot 3^{20}+7 \cdot 3^{19}\right) \cdot 57}{\left(19 \cdot 27^{4}\right)^{2}}$.
6. Сократите дробь: $\frac{a^{2}-4 a b+4 b^{2}}{4 b^{2}-a^{2}}$.
7. Решите графически систему уравнений $\left\{\begin{array}{c}5 x+2 y=-3 \\ 2 x+5 y=3\end{array}\right.$,
8. Расстояние $A B$ равно 340 км. Из $A$ и $B$ одновременно навстречу друг другу выехали два поезда. $V_{A}$ меньше $V_{B}$ на 5 км/ч. Найдите скорости поездов, если через 2 часа между ними было 30 км.
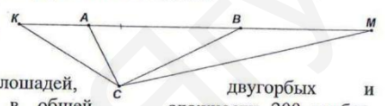
9. В треугольнике $A B C$ $\angle C=90^{\circ}, A K=A C ; B M$ = BC. Найдите $\angle K C M$.
   
10. В стаде, состоящем из лошадей, одногорбых верблюдов, в общей с сложности 200 горбов. Сколько животных в стаде, если количество лошадей равно количеству двугорбых верблюдов?

Решения задач

1. Вычислите: $\left(-6 \frac{7}{8}+1,375-5 \frac{1}{2} \cdot 0,73\right):(-1,73)$.
   Решение:
   Переведём смешанные числа в десятичные дроби:
   $-6\frac{7}{8} = -6.875$; $5\frac{1}{2} = 5.5$
   Выполним действия по порядку:
   $5.5 \cdot 0.73 = 4.015$
   $-6.875 + 1.375 = -5.5$
   $-5.5 - 4.015 = -9.515$
   $-9.515 : (-1.73) = 5.5$
   Ответ: 5,5.
   
   
2. Сумма трех чисел равна 80. Первое число составляет $20 \%$ всей суммы, но $40 \%$ второго числа. Найдите среднее арифметическое первого и третьего чисел.
   Решение:
   Первое число: $80 \cdot 0.2 = 16$
   Второе число: $16 : 0.4 = 40$
   Третье число: $80 - 16 - 40 = 24$
   Среднее арифметическое: $\frac{16 + 24}{2} = 20$
   Ответ: 20.
   
   
3. Решите уравнение: $\frac{3 + 2x}{3} - \left(\frac{1+x}{5} - \frac{1-x}{6}\right) = 1$.
   Решение:
   Умножим обе части на 30 (НОК знаменателей):
   $10(3 + 2x) - 6(1 + x) + 5(1 - x) = 30$
   Раскроем скобки:
   $30 + 20x - 6 - 6x + 5 - 5x = 30$
   Упростим:
   $9x + 29 = 30 \quad \Rightarrow \quad 9x = 1 \quad \Rightarrow \quad x = \frac{1}{9}$
   Ответ: $\frac{1}{9}$.
   
   
4. Решите уравнение: $x^{3} - x^{2} - x + 1 = 0$.
   Решение:
   Разложим на множители:
   $(x^3 - x^2) - (x - 1) = x^2(x - 1) - (x - 1) = (x - 1)(x^2 - 1) = (x - 1)^2(x + 1)$
   Корни: $x = 1$ (двойной), $x = -1$
   Ответ: $-1; 1$.
   
   
5. Найдите значение выражения: $\frac{\left(4 \cdot 3^{20} + 7 \cdot 3^{19}\right) \cdot 57}{\left(19 \cdot 27^{4}\right)^{2}}$.
   Решение:
   Упростим числитель:
   $3^{19}(4 \cdot 3 + 7) \cdot 57 = 3^{19} \cdot 19 \cdot 57$
   Знаменатель:
   $(19 \cdot 3^{12})^2 = 19^2 \cdot 3^{24}$
   Сократим:
   $\frac{3^{19} \cdot 19 \cdot 57}{19^2 \cdot 3^{24}} = \frac{57}{19} \cdot 3^{-5} = 3 \cdot \frac{1}{243} = \frac{1}{81}$
   Ответ: $\frac{1}{81}$.
   
   
6. Сократите дробь: $\frac{a^{2} - 4ab + 4b^{2}}{4b^{2} - a^{2}}$.
   Решение:
   Числитель: $(a - 2b)^2$
   Знаменатель: $(2b - a)(2b + a)$
   Сократим:
   $\frac{(a - 2b)^2}{-(a - 2b)(a + 2b)} = -\frac{a - 2b}{a + 2b}$
   Ответ: $-\frac{a - 2b}{a + 2b}$.
   
   
7. Решите графически систему уравнений $\left\{\begin{array}{c}5x + 2y = -3 \\ 2x + 5y = 3\end{array}\right.$.
   Решение:
   Приведём уравнения к виду $y = kx + b$:
   1) $2y = -5x - 3 \quad \Rightarrow \quad y = -2.5x - 1.5$
   2) $5y = -2x + 3 \quad \Rightarrow \quad y = -0.4x + 0.6$
   Точка пересечения: $(-1, 1)$
   Ответ: $(-1; 1)$.
   
   
8. Расстояние $AB$ равно 340 км. Из $A$ и $B$ одновременно навстречу друг другу выехали два поезда. Скорость первого меньше скорости второго на 5 км/ч. Найдите скорости поездов, если через 2 часа между ними было 30 км.
   Решение:
   Пусть $v$ — скорость первого поезда, тогда $(v + 5)$ — скорость второго.
   За 2 часа они проехали: $2v + 2(v + 5) = 340 - 30 = 310$ км
   Уравнение: $4v + 10 = 310 \quad \Rightarrow \quad v = 75$ км/ч
   Скорости: 75 км/ч и 80 км/ч
   Ответ: 75 км/ч и 80 км/ч.
   
   
9. В треугольнике $ABC$ $\angle C = 90^{\circ}$, $AK = AC$; $BM = BC$. Найдите $\angle KCM$.
   Решение:
   $\triangle ACK$ и $\triangle BCM$ — равнобедренные.
   $\angle ACK = \frac{180^\circ - 45^\circ}{2} = 67.5^\circ$
   $\angle BCM = \frac{180^\circ - 45^\circ}{2} = 67.5^\circ$
   $\angle KCM = 67.5^\circ + 67.5^\circ - 90^\circ = 45^\circ$
   Ответ: $45^\circ$.
   
   
10. В стаде, состоящем из лошадей, одногорбых верблюдов, в общей сложности 200 горбов. Сколько животных в стаде, если количество лошадей равно количеству двугорбых верблюдов?
    Решение:
    Пусть $x$ — количество лошадей и двугорбых верблюдов.
    Одногорбых верблюдов: $200 - 2x$
    Общее количество животных: $x + x + (200 - 2x) = 200$
    Ответ: 200.