8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1580 из 7 в 8 класс 2008 год (вариант 5)

Школа:
Сложность:
Дата экзамена: 2008
Школа:
Сложность:
Дата экзамена: 2008
youit.school ©

ЛИЦЕЙ №1580


2008 год


Вариант 5



  1. Упростите выражение: $\left(\frac{1}{x^{2}}+\frac{9}{y^{2}}+\frac{2}{x+y} \cdot \frac{3 x+3 y}{x y}\right) \cdot \frac{x^{2} y^{2}}{9 x^{2}-y^{2}}$.
  2. Упростите выражение, разложив числитель и знаменатель на множители, и вычислите его при $a=-3$:
    $\frac{a x-2 a y+2 x-4 y}{a x+x-2 a y-2 y}$
  3. В агрофирме площадь полей картофеля на $150 \%$ больше, чем у фермера, а урожайность полей - на 30% меньше, чем у фермера. На сколько процентов урожай картофеля агрофирмы больше, чем у фермера?
  4. Расстояние по реке между пунктами А и В равно 42 км. Путь между А и В по течению реки катер проходит за 3 часа, а обратный путь (против течения) - за 7 часов. Определите собственную скорость катера и скорость течения реки.
  5. Решите уравнение: $\frac{x-2}{5}-\frac{3 x+2}{6}=\frac{2}{3}-x$.
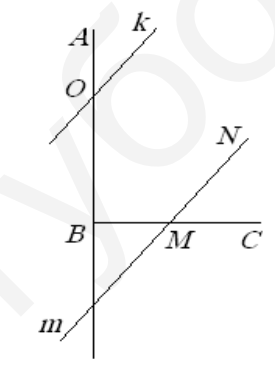
  6. Дан прямой угол $A B C .$ Прямая $\boldsymbol{k}$ пересекает луч $B A$ и составляет с ним угол $29^{\circ} .$ Прямая $\boldsymbol{m}$ пересекает луч $B C$ и параллельна $\boldsymbol{k} .$ Какой угол составляет $\boldsymbol{m}$ с $B C ?$
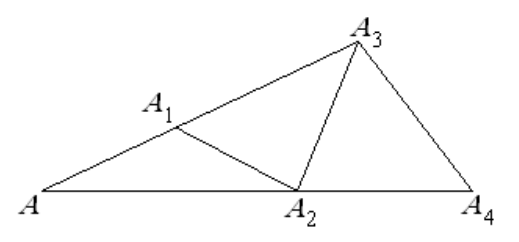
  7. На одной стороне угла величиной $34^{\circ}$ с вершиной $A$ выбраны точки $A_{1}$ и $A_{3}$, а на другой точки $A_{2}$ и $A_{4}$, так что $A A_{1}=A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{4} .$ Найти угол $A A_{4} A_{3} .$
  8. Какой треугольник называется равнобедренным, равносторонним? Теорема о свойствах углов равнобедренного треугольника. Признак равнобедренного треугольника. Свойство медианы равнобедренного треугольника.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите выражение: $\left(\frac{1}{x^{2}}+\frac{9}{y^{2}}+\frac{2}{x+y} \cdot \frac{3 x+3 y}{x y}\right) \cdot \frac{x^{2} y^{2}}{9 x^{2}-y^{2}}$.
    Решение: Упростим выражение по частям:
    $\frac{2}{x+y} \cdot \frac{3x + 3y}{xy} = \frac{2}{x+y} \cdot \frac{3(x + y)}{xy} = \frac{6}{xy}$
    Теперь сложим все слагаемые в скобках:
    $\frac{1}{x^2} + \frac{9}{y^2} + \frac{6}{xy} = \left(\frac{1}{x} + \frac{3}{y}\right)^2$
    Знаменатель преобразуем по формуле разности квадратов:
    $9x^2 - y^2 = (3x - y)(3x + y)$
    Подставим в исходное выражение:
    $\left(\frac{1}{x} + \frac{3}{y}\right)^2 \cdot \frac{x^2 y^2}{(3x - y)(3x + y)} = \frac{(y + 3x)^2}{x^2 y^2} \cdot \frac{x^2 y^2}{(3x - y)(3x + y)} = \frac{(3x + y)^2}{(3x - y)(3x + y)} = \frac{3x + y}{3x - y}$
    Ответ: $\frac{3x + y}{3x - y}$.

  2. Упростите выражение, разложив числитель и знаменатель на множители, и вычислите его при $a=-3$: $\frac{a x-2 a y+2 x-4 y}{a x+x-2 a y-2 y}$
    Решение: Разложим числитель и знаменатель на множители:
    Числитель: $a x - 2a y + 2x - 4y = a(x - 2y) + 2(x - 2y) = (a + 2)(x - 2y)$
    Знаменатель: $a x + x - 2a y - 2y = x(a + 1) - 2y(a + 1) = (a + 1)(x - 2y)$
    После сокращения: $\frac{(a + 2)(x - 2y)}{(a + 1)(x - 2y)} = \frac{a + 2}{a + 1}$
    При $a = -3$: $\frac{-3 + 2}{-3 + 1} = \frac{-1}{-2} = 0,5$
    Ответ: 0,5.

  3. В агрофирме площадь полей картофеля на $150 \%$ больше, чем у фермера, а урожайность полей - на 30% меньше, чем у фермера. На сколько процентов урожай картофеля агрофирмы больше, чем у фермера?
    Решение: Пусть у фермера площадь $S$ и урожайность $U$. Тогда:
    Площадь агрофирмы: $S + 1,5S = 2,5S$
    Урожайность агрофирмы: $U - 0,3U = 0,7U$
    Урожай фермера: $S \cdot U$
    Урожай агрофирмы: $2,5S \cdot 0,7U = 1,75SU$
    Разница: $\frac{1,75SU - SU}{SU} \cdot 100% = 75\%$
    Ответ: на 75%.

  4. Расстояние по реке между пунктами А и В равно 42 км. Путь между А и В по течению реки катер проходит за 3 часа, а обратный путь (против течения) - за 7 часов. Определите собственную скорость катера и скорость течения реки.
    Решение: Пусть $v$ — собственная скорость катера (км/ч), $u$ — скорость течения (км/ч). Составим систему уравнений:
    $\begin{cases} (v + u) \cdot 3 = 42 \\ (v - u) \cdot 7 = 42 \end{cases}$
    Решим уравнения:
    $v + u = 14$
    $v - u = 6$
    Сложим уравнения: $2v = 20 \Rightarrow v = 10$ км/ч
    Вычтем уравнения: $2u = 8 \Rightarrow u = 4$ км/ч
    Ответ: 10 км/ч и 4 км/ч.

  5. Решите уравнение: $\frac{x-2}{5}-\frac{3 x+2}{6}=\frac{2}{3}-x$.
    Решение: Умножим обе части на 30 (НОК знаменателей):
    $6(x - 2) - 5(3x + 2) = 20 - 30x$
    $6x - 12 - 15x - 10 = 20 - 30x$
    $-9x - 22 = 20 - 30x$
    $21x = 42$
    $x = 2$
    Ответ: 2.

  6. Дан прямой угол $A B C .$ Прямая $\boldsymbol{k}$ пересекает луч $B A$ и составляет с ним угол $29^{\circ} .$ Прямая $\boldsymbol{m}$ пересекает луч $B C$ и параллельна $\boldsymbol{k} .$ Какой угол составляет $\boldsymbol{m}$ с $B C ?$
    Решение: Так как прямые $k$ и $m$ параллельны, а угол между $k$ и $BA$ равен $29^\circ$, то угол между $m$ и $BC$ будет равен $90^\circ - 29^\circ = 61^\circ$ (как соответственный угол при параллельных прямых).
    Ответ: $61^\circ$.

  7. На одной стороне угла величиной $34^{\circ}$ с вершиной $A$ выбраны точки $A_{1}$ и $A_{3}$, а на другой точки $A_{2}$ и $A_{4}$, так что $A A_{1}=A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{4} .$ Найти угол $A A_{4} A_{3} .$
    Решение: Построим последовательно равные отрезки. Рассмотрим треугольники $AA_1A_2$, $A_1A_2A_3$ и т.д. Каждый следующий треугольник будет подобен предыдущему с коэффициентом 1. Угол при вершине $A$ равен $34^\circ$, поэтому угол $AA_4A_3$ будет равен $34^\circ$ как соответственный в подобных треугольниках.
    Ответ: $34^\circ$.

  8. Какой треугольник называется равнобедренным, равносторонним? Теорема о свойствах углов равнобедренного треугольника. Признак равнобедренного треугольника. Свойство медианы равнобедренного треугольника.
    Решение:
    1. Равнобедренный треугольник — треугольник с двумя равными сторонами. Равносторонний треугольник — треугольник, у которого все стороны равны.
    2. Теорема: В равнобедренном треугольнике углы при основании равны.
    3. Признак: Если в треугольнике два угла равны, то он равнобедренный.
    4. Свойство медианы: В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно высотой и биссектрисой.
Материалы школы Юайти