Лицей №1580 из 7 в 8 класс 2012 год (вариант 4)

ЛИЦЕЙ №1580

2012 год

1. Разложите выражение на множители:
   $x(m-n)+y(m-n)$
   (2 балла)
2. Упростите выражение и вычислите его значение при заданных $a$ и $b$ :
   $\frac{25 a^{2}+30 a b+9 b^{2}}{25 a^{2}-9 b^{2}}, a=2, b=-1$
   (2 балла)
3. Вычислите:
   $\left(8^{3} \cdot(-3)^{3}\right): 6^{3}$
   (2 балла)
4. Решите уравнение: $\frac{5 x-9}{4}+\frac{5 x-7}{3}=1$
5. Со скоростью 80 км/час товарный поезд прошел 720 км. Какое расстояние пройдет за то же время пассажирский поезд, скорость которого 60 км/час? (2 балла)
6. Вычислите: $564 \cdot 645-563 \cdot 645+563355$ (2 балла)
7. Из равенства выразите сначала $x$ через $y$, а затем $y$ через $x$ :
   $2 x+3 y=6$
   (2 балла)
8. До какой массы надо выпарить 600 грамм $15 \%$-го раствора соли, чтобы получить $20 \%$-й раствор соли? (2 балла)
9. Периметр равнобедренного треугольника равен 45 см, а боковая сторона меньше основания на 3 см. Найти стороны этого треугольника. (3 балла)
10. Найти: $\angle A B C$.
    
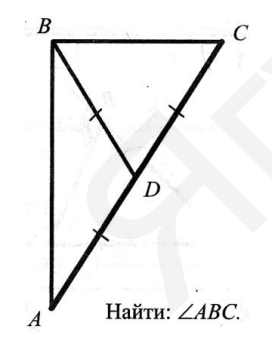
    (3 балла)
11. Вычислите
    $\frac{\left(\frac{5}{8}+2 \frac{17}{24}\right): 2,5}{\left(1,3+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}} \cdot 0,5$
    (4 балла)
12. Найти $x$.
    
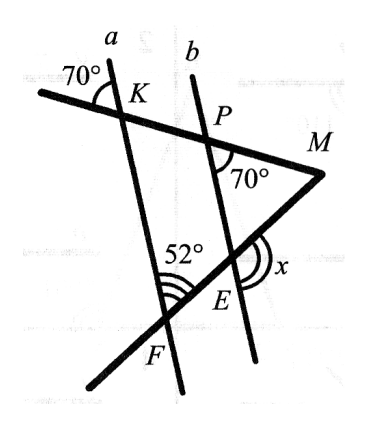
    (4 балла)

Решения задач

1. Разложите выражение на множители:
   $x(m-n)+y(m-n)$
   Решение: Вынесем общий множитель $(m - n)$ за скобки:
   $(m - n)(x + y)$
   Ответ: $(m - n)(x + y)$.
   
   
2. Упростите выражение и вычислите его значение при заданных $a$ и $b$ :
   $\frac{25 a^{2}+30 a b+9 b^{2}}{25 a^{2}-9 b^{2}}$, $\quad a=2$, $\quad b=-1$
   Решение: Числитель — квадрат суммы: $(5a + 3b)^2$, знаменатель — разность квадратов: $(5a - 3b)(5a + 3b)$. Сократим:
   $\frac{(5a + 3b)^2}{(5a - 3b)(5a + 3b)} = \frac{5a + 3b}{5a - 3b}$
   Подставим значения:
   $\frac{5 \cdot 2 + 3 \cdot (-1)}{5 \cdot 2 - 3 \cdot (-1)} = \frac{10 - 3}{10 + 3} = \frac{7}{13}$
   Ответ: $\frac{7}{13}$.
   
   
3. Вычислите:
   $\left(8^{3} \cdot(-3)^{3}\right): 6^{3}$
   Решение: Представим выражение в виде:
   $\left(\frac{8 \cdot (-3)}{6}\right)^3 = (-4)^3 = -64$
   Ответ: $-64$.
   
   
4. Решите уравнение: $\frac{5 x-9}{4}+\frac{5 x-7}{3}=1$
   Решение: Умножим обе части на 12:
   $3(5x - 9) + 4(5x - 7) = 12$
   $15x - 27 + 20x - 28 = 12$
   $35x - 55 = 12 \quad \Rightarrow \quad 35x = 67 \quad \Rightarrow \quad x = \frac{67}{35}$
   Ответ: $\frac{67}{35}$.
   
   
5. Со скоростью 80 км/час товарный поезд прошел 720 км. Какое расстояние пройдет за то же время пассажирский поезд, скорость которого 60 км/часшение: Вшение: Время движения товарного поезда:
   $t = \frac{720}{80} = 9$ часов
   Расстояние для пассажирского поезда:
   $S = 60 \cdot 9 = 540$ км
   Ответ: 540 км.
   
   
6. Вычислите: $564 \cdot 645 - 563 \cdot 645 + 563355$
   Решение: Вынесем общий множитель:
   $645(564 - 563) + 563355 = 645 \cdot 1 + 563355 = 645 + 563355 = 564000$
   Ответ: 564000.
   
   
7. Из равенства выразите сначала $x$ через $y$, а затем $y$ через $x$ :
   $2x+3y=6$
   Решение:
   $x = \frac{6 - 3y}{2}$;
   $y = \frac{6 - 2x}{3}$
   Ответ: $x = \frac{6 - 3y}{2}$; $y = \frac{6 - 2x}{3}$.
   
   
8. До какой массы надо выпарить 600 грамм $15 \%$-го раствора соли, чтобы получить $20 \%$-й раствор соли? Решение: Масса соли в исходном растворе:
   $600 \cdot 0,15 = 90$ г
   Новая масса раствора:
   $m = \frac{90}{0,2} = 450$ г
   Ответ: 450 г.
   
   
9. Периметр равнобедренного треугольника равен 45 см, а боковая сторона меньше основания на 3 см. Найти стороны этого треугольника. Решение: Пусть боковая сторона — $x$, тогда основание — $x + 3$:
   $2x + (x + 3) = 45 \quad \Rightarrow \quad 3x = 42 \quad \Rightarrow \quad x = 14$ см
   Стороны: 14 см, 14 см, 17 см
   Ответ: 14 см, 14 см, 17 см.
   
   
10. Найти: $\angle A B C$. Решение: Поскольку $\angle ABC$ опирается на диаметр окружности, он является прямым:
    $\angle ABC = 90^{\circ}$
    Ответ: $90^{\circ}$.
    
    
11. Вычислите
    $\frac{\left(\frac{5}{8}+2 \frac{17}{24}\right): 2,5}{\left(1,3+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}} \cdot 0,5$
    Решение:
    Числитель: $\left(\frac{5}{8} + \frac{65}{24}\right) : 2,5 = \frac{80}{24} : \frac{5}{2} = \frac{10}{3} \cdot \frac{2}{5} = \frac{4}{3}$
    Знаменатель: $\left(\frac{13}{10} + \frac{23}{30} + \frac{4}{11}\right) \cdot \frac{110}{401} = \frac{401}{165} \cdot \frac{110}{401} = \frac{2}{3}$
    Результат: $\frac{\frac{4}{3}}{\frac{2}{3}} \cdot 0,5 = 2 \cdot 0,5 = 1$
    Ответ: 1.
    
    
12. Найти $x$. Решение: По теореме о сумме углов треугольника:
    $x + 26^{\circ} + 26^{\circ} = 180^{\circ} \quad \Rightarrow \quad x = 128^{\circ}$
    Ответ: $128^{\circ}$.