Лицей №1580 из 7 в 8 класс 2012 год вариант 3

ЛИЦЕЙ №1580

2012 год

1. Разложите выражение на множители:
   $a^{4}+2 a^{3}-a-2$
   (2 балла).
2. Упростите выражение и вычислите его значение при заданном значении $a$ :
   $2 a-(3 a-(4 a-5)), a=2$
   (2 балла).
3. Вычислите: $\quad \frac{1,2 \cdot 0,6-1,2}{1-0,2^{2}}$. (2 балла).
4. $\quad$ Решите уравнение: $\frac{1}{2}(x-3)=\frac{1}{3}(9-x)$. (2 балла).
5. Некоторое число сначала уменьшили на $10 \%$, а затем полученный результат увеличили на $40 % .$ В результате получилось $189 .$ Чему равно исходное число? (2 балла).
6. Решите систему уравнений: $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=3 \\ \frac{1}{x}-\frac{1}{y}=1\end{array}\right.$ (2 балла).
7. Вычислите: $\frac{73^{2}-2 \cdot 73 \cdot 23+23^{2}}{26^{2}-24^{2}}$. (2 балла).
8. Сумма двух чисел равна 77. Найдите эти числа, если $\frac{2}{3}$ одного числа равна $\frac{4}{5}$. (2 балла).
9. Отрезок DM - биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если угол CDE равен $68^{0} .$ (3 балла).
10. Задайте формулой линейную функцию, если известно, что ее график проходит через точку $\mathrm{M}(1 ; 4)$ и не пересекает график функции $y=-3 x+1580$. (3 балла)
11. Вычислите: $1 \frac{7}{20}: 2,7+2,7: 1,35+\left(0,4: 2 \frac{1}{2}\right) \cdot\left(4,2-1 \frac{3}{40}\right)$ (4 балла)
12. На сторонах угла A, равного $127^{\circ}$, отмечены точки В и С, а внутри угла точка D так, что угол ABD равен $25^{\circ}$, угол ACD равен $19^{\circ}$. Найдите угол BDC.
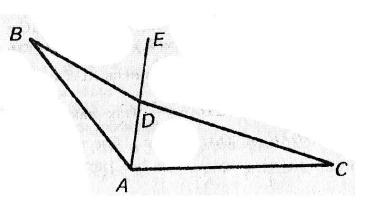    (4 балла)

Решения задач

1. Разложите выражение на множители: $a^{4}+2 a^{3}-a-2$ Решение: Сгруппируем слагаемые:
   $(a^{4} + 2a^{3}) - (a + 2) = a^{3}(a + 2) - 1(a + 2) = (a^{3} - 1)(a + 2)$
   Разложим $a^{3} - 1$ по формуле разности кубов:
   $(a - 1)(a^{2} + a + 1)(a + 2)$
   Ответ: $(a-1)(a+2)\left(a^{2}+a+1\right)$.
   
   
2. Упростите выражение и вычислите его значение при заданном значении $a$: $2 a-(3 a-(4 a-5)), a=2$ Решение: Раскроем скобки последовательно:
   $2a - (3a - 4a + 5) = 2a - (-a + 5) = 2a + a - 5 = 3a - 5$
   Подставим $a = 2$:
   $3 \cdot 2 - 5 = 6 - 5 = 1$
   Ответ: $3 a-5=1$.
   
   
3. Вычислите: $\quad \frac{1,2 \cdot 0,6-1,2}{1-0,2^{2}}$
   Решение: Вычислим числитель и знаменатель отдельно:
   Числитель: $1,2 \cdot 0,6 - 1,2 = 0,72 - 1,2 = -0,48$
   Знаменатель: $1 - 0,2^{2} = 1 - 0,04 = 0,96$
   Результат: $\frac{-0,48}{0,96} = -0,5$
   Ответ: -0,5.
   
   
4. Решите уравнение: $\frac{1}{2}(x-3)=\frac{1}{3}(9-x)$
   Решение: Умножим обе части на 6 для устранения знаменателей:
   $3(x - 3) = 2(9 - x)$
   $3x - 9 = 18 - 2x$
   $5x = 27 \quad \Rightarrow \quad x = \frac{27}{5} = 5,4$
   Ответ: 5,4.
   
   
5. Некоторое число сначала уменьшили на $10 \%$, а затем полученный результат увеличили на $40 % .$ В результате получилось $189 .$ Чему равно исходное число?
   Решение: Пусть исходное число — $x$. После изменений:
   $x \cdot 0,9 \cdot 1,4 = 189$
   $1,26x = 189 \quad \Rightarrow \quad x = \frac{189}{1,26} = 150$
   Ответ: 150.
   
   
6. Решите систему уравнений: $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=3 \\ \frac{1}{x}-\frac{1}{y}=1\end{array}\right.$
   Решение: Сложим и вычтем уравнения:
   $\frac{2}{x} = 4 \quad \Rightarrow \quad x = 0,5$
   $\frac{2}{y} = 2 \quad \Rightarrow \quad y = 1$
   Ответ: $0,5; 1$.
   
   
7. Вычислите: $\frac{73^{2}-2 \cdot 73 \cdot 23+23^{2}}{26^{2}-24^{2}}$
   Решение: Числитель — квадрат разности:
   $(73 - 23)^{2} = 50^{2} = 2500$
   Знаменатель — разность квадратов:
   $(26 - 24)(26 + 24) = 2 \cdot 50 = 100$
   Результат: $\frac{2500}{100} = 25$
   Ответ: 25.
   
   
8. Сумма двух чисел равна 77. Найдите эти числа, если $\frac{2}{3}$ одного числа равна $\frac{4}{5}$ другого.
   Решение: Пусть числа $a$ и $b$:
   $\begin{cases} a + b = 77 \\ \frac{2}{3}a = \frac{4}{5}b \end{cases}$
   Из второго уравнения: $10a = 12b \quad \Rightarrow \quad a = \frac{6}{5}b$
   Подставим в первое уравнение:
   $\frac{6}{5}b + b = 77 \quad \Rightarrow \quad \frac{11}{5}b = 77 \quad \Rightarrow \quad b = 35$
   Тогда $a = 77 - 35 = 42$
   Ответ: 35;42.
   
   
9. Задайте формулой линейную функцию, если известно, что ее график проходит через точку $\mathrm{M}(1 ; 4)$ и не пересекает график функции $y=-3 x+1580$.
   Решение: Угловой коэффициент параллельной прямой: $k = -3$.
   Подставим точку M: $4 = -3 \cdot 1 + b \quad \Rightarrow \quad b = 7$
   Уравнение: $y = -3x + 7$
   Ответ: $y=-3 x+7$.
   
   
10. Вычислите: $1 \frac{7}{20}: 2,7+2,7: 1,35+\left(0,4: 2 \frac{1}{2}\right) \cdot\left(4,2-1 \frac{3}{40}\right)$
    Решение: Разделим на части:
    $1\frac{7}{20} : 2,7 = \frac{27}{20} : \frac{27}{10} = 0,5$
    $2,7 : 1,35 = 2$
    $0,4 : 2\frac{1}{2} = 0,4 : 2,5 = 0,16$
    $4,2 - 1\frac{3}{40} = 4,2 - 1,075 = 3,125$
    Результат: $0,5 + 2 + 0,16 \cdot 3,125 = 0,5 + 2 + 0,5 = 3$
    Ответ: 3.